K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
giúp em với mn ơi,e đag cần gấp, mn giúp em với ạ
31 tháng 10 2021
a: Xét ΔBAC có
D là trung điểm của AB
M là trung điểm của AC
Do đó: DM là đường trung bình của ΔABC
Suy ra: DM//BC và \(DM=\dfrac{BC}{2}=3.5\left(cm\right)\)
12 tháng 3 2022
a, \(40x-20+45x-30=48x-36\Leftrightarrow37x=14\Leftrightarrow x=\dfrac{14}{37}\)
b, đk : x khác -3 ; 3
\(5x+15+4x-12=x-5\Leftrightarrow8x=-38\Leftrightarrow x=-\dfrac{19}{4}\)(tm)
c, \(\left[{}\begin{matrix}2x+3=0\\3x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=\dfrac{1}{3}\end{matrix}\right.\)
8 tháng 5 2021
ĐKXĐ: \(x\notin\left\{0;-9\right\}\)
Ta có: \(\dfrac{1}{x+9}-\dfrac{1}{x}=\dfrac{1}{5}+\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{20x}{20x\left(x+9\right)}-\dfrac{20\left(x+9\right)}{20x\left(x+9\right)}=\dfrac{4x\left(x+9\right)+5x\left(x+9\right)}{20x\left(x+9\right)}\)
Suy ra: \(4x^2+36x+5x^2+45x=20x-20x-180\)
\(\Leftrightarrow9x^2+81x+180=0\)
\(\Leftrightarrow x^2+9x+20=0\)
\(\Leftrightarrow x^2+4x+5x+20=0\)
\(\Leftrightarrow x\left(x+4\right)+5\left(x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\left(nhận\right)\\x=-5\left(nhận\right)\end{matrix}\right.\)
Vậy: S={-4;-5}
NT
3
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 12 2023
câu a, \(\dfrac{x}{x+1}\); \(\dfrac{x^2}{1-x}\); \(\dfrac{1}{x^2-1}\) (đk \(x\)≠ -1; 1)
\(x^2\) - 1 = ( \(x\) - 1).(\(x\) + 1)
\(\dfrac{x}{x+1}\) = \(\dfrac{x.\left(x-1\right)}{\left(x+1\right).\left(x-1\right)}\);
\(\dfrac{x^2}{1-x}\) = \(\dfrac{-x^2}{x-1}\)= \(\dfrac{-x^2.\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)
\(\dfrac{1}{x^2-1}\) = \(\dfrac{1}{\left(x-1\right)\left(x+1\right)}\)
b, \(\dfrac{10}{x+2}\); \(\dfrac{5}{2x-4}\); \(\dfrac{1}{6-3x}\) (đk \(x\) ≠ -2; 2)
2\(x-4\) = 2.(\(x\) - 2); 6 - 3\(x\) = - 3.(\(x\) - 2)
\(\dfrac{10}{x+2}\) = \(\dfrac{10.2.3\left(x-2\right)}{2.3\left(x+2\right)\left(x-2\right)}\) = \(\dfrac{60\left(x-2\right)}{6\left(x-2\right)\left(x+2\right)}\)
\(\dfrac{5}{2x-4}\) = \(\dfrac{5.3\left(x+2\right)}{2.3\left(x-2\right).\left(x+2\right)}\) = \(\dfrac{15.\left(x+2\right)}{6.\left(x-2\right)\left(x+2\right)}\)
\(\dfrac{1}{6-3x}\) = \(\dfrac{-1}{3.\left(x-2\right)}\) = \(\dfrac{-1.\left(x+2\right)}{3.2.\left(x-2\right)\left(x+2\right)}\) = \(\dfrac{-2.\left(x+2\right)}{6.\left(x-2\right).\left(x+2\right)}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 12 2023
c, \(\dfrac{x}{2x-4}\); \(\dfrac{1}{2x+4}\) và \(\dfrac{3}{4-x^2}\) đk \(x\) ≠ 2; -2
\(\dfrac{x}{2x-4}\) = \(\dfrac{x}{2.\left(x-2\right)}\) = \(\dfrac{x.\left(x+2\right)}{2.\left(x-2\right).\left(x+2\right)}\)
\(\dfrac{1}{2x+4}\) = \(\dfrac{1}{2.\left(x+2\right)}\) = \(\dfrac{\left(x-2\right)}{2.\left(x+2\right).\left(x-2\right)}\)
\(\dfrac{3}{4-x^2}\) = \(\dfrac{-3}{\left(x-2\right)\left(x+2\right)}\) = \(\dfrac{-6}{2.\left(x-2\right)\left(x+2\right)}\)
30 tháng 10 2021
a, Vì D,M là trung điểm AB,AC nên DM là đtb tg ABC
Do đó \(DM=\dfrac{1}{2}BC=\dfrac{7}{2}\left(cm\right)\) và DM//BC
KH
8 tháng 5 2021
Hướng làm:
Thấy cả tử mẫu cộng lại đều bằng 2021 → Cộng thêm 1 rồi quy đồng với mỗi phân thức
\(\dfrac{x+2}{2019}+1+\dfrac{x+3}{2018}+1=\dfrac{x+4}{2017}+1+\dfrac{x}{2021}+1\\ \Leftrightarrow\dfrac{x+2021}{2019}+\dfrac{x+2021}{2018}-\dfrac{x+2021}{2017}-\dfrac{x+2021}{2021}=0\\ \Leftrightarrow\left(x+2021\right)\left(\dfrac{1}{2019}+\dfrac{1}{2018}-\dfrac{1}{2017}-\dfrac{1}{2021}\right)=0\\ \Leftrightarrow x+2021=0\Leftrightarrow x=-2021\)
TM
8 tháng 5 2021
\(< =>\dfrac{x+2}{2019}+1+\dfrac{x+3}{2018}+1=\dfrac{x+4}{2017}+1+\dfrac{x}{2021}+1\)
\(< =>\dfrac{x+2+2019}{2019}+\dfrac{x+3+2018}{2018}=\dfrac{x+4+2017}{2017}+\dfrac{x+2021}{2021}\)
\(< =>\dfrac{x+2021}{2019}+\dfrac{x+2021}{2018}-\dfrac{x+2021}{2017}-\dfrac{x+2021}{2021}=0\)
\(< =>\left(x+2021\right)\left(\dfrac{1}{2019}+\dfrac{1}{2018}-\dfrac{1}{2017}-\dfrac{1}{2021}=\right)=0\)
\(< =>x+2021=0< =>x=-2021\)
Vậy....
MA
2
23 tháng 12 2021
g: \(=\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\)
h: \(=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)
23 tháng 12 2021
\(e,=\dfrac{1}{x-1}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x^2-2x+1}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{\left(x-1\right)^2}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x-1}{x^2+1}\\ f,=\dfrac{3x-1}{2\left(3x+1\right)}+\dfrac{3x+1}{2\left(3x-1\right)}-\dfrac{6x}{\left(3x-1\right)\left(3x+1\right)}\\ =\dfrac{9x^2-6x+1+9x^2+6x+1-12x}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{2\left(3x-1\right)^2}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{3x-1}{3x+1}\)
\(g,=\dfrac{x}{x\left(x-2\right)}-\dfrac{x^2+4x}{x\left(x-2\right)\left(x+2\right)}-\dfrac{2}{x\left(x+2\right)}\\ =\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\\ h,=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)
DD
Đoàn Đức Hà
Giáo viên
8 tháng 5 2021
\(\frac{x+2}{2019}+\frac{x+3}{2018}=\frac{x+4}{2017}+\frac{x}{2021}\)
\(\Leftrightarrow\frac{x+2}{2019}+1+\frac{x+3}{2018}+1=\frac{x+4}{2017}+1+\frac{x}{2021}+1\)
\(\Leftrightarrow\frac{x+2021}{2019}+\frac{x+2021}{2018}=\frac{x+2021}{2017}+\frac{x+2021}{2021}\)
\(\Leftrightarrow x+2021=0\)
\(\Leftrightarrow x=-2021\)
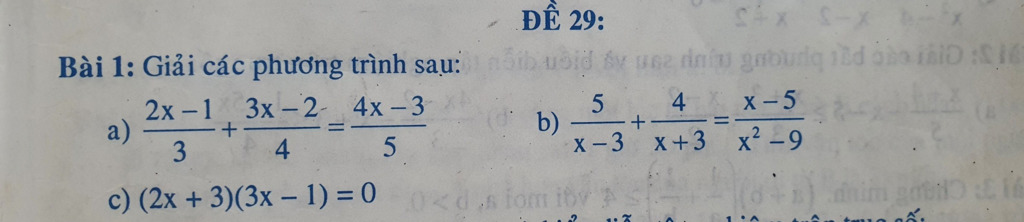
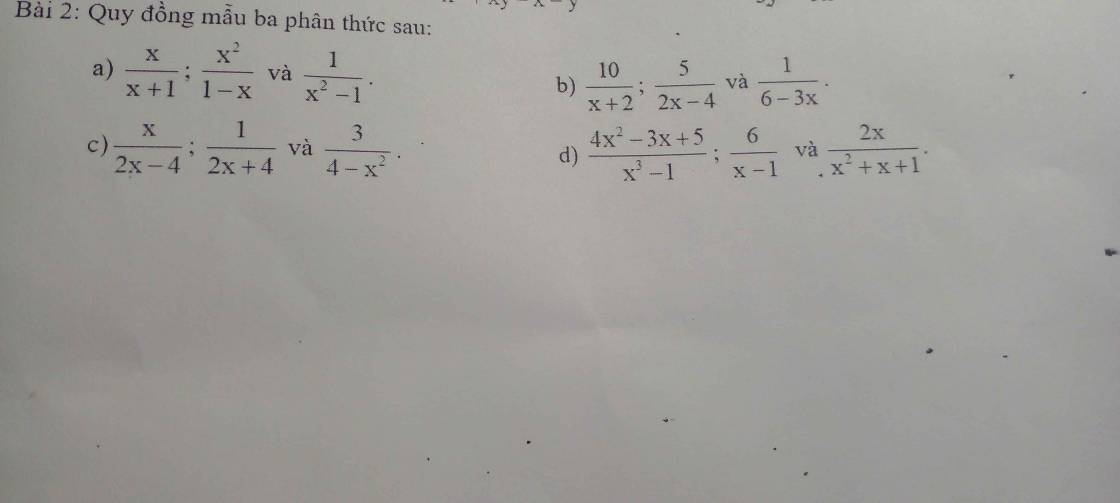
9:
a: XétΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>BA/BH=BC/BA
=>BA^2=BH*BC
b: BC=25cm; AB=căn 9*25=15cm; AC=căn 16*25=20cm
S ABC=1/2*15*20=150cm2
C ABC=25+15+20=60cm