Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\left(\dfrac{\sqrt{x}-2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}+2}{x-1}\right):\dfrac{2\sqrt{x}}{x-1}\)
\(=\left(\dfrac{\sqrt{x}-2}{\sqrt{x}^2+2\sqrt{x}+1^2}-\dfrac{\sqrt{x}+2}{\sqrt{x}^2-1^2}\right).\dfrac{x-1}{2\sqrt{x}}\)
\(=\left(\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right).\dfrac{x-1}{2\sqrt{x}}\)
Tới đây là có được mẫu chung ở dấu = thứ 2 rồi.
\(A=\left(\dfrac{\sqrt{x}-2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}+2}{x-1}\right):\dfrac{2\sqrt{x}}{x-1}\) ( với x>0;\(x\ne1\) )
\(=\left[\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right].\dfrac{x-1}{2\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(x-1\right)}.\dfrac{x-1}{2\sqrt{x}}\)
\(=.....\) ( theo như trên )


x + 3y = x(5y - 1) (1)
1/x - 3/y = -2 (2)
(1) ⇔ x(5y - 1) - x = 3y
⇔ x(5y - 2) = 3y
⇔ x = 3y/(5y - 2) (3)
Thế (3) vào (2) ta được:
(2) ⇔ 1/[3y/(5y - 2)] - 3/y = -2
⇔ (5y - 2)/3y - 3/y = -2
⇔ 5y - 2 - 9 = -6y
⇔ 5y + 6y = 11
⇔ 11y = 11
⇔ y = 1 thế vào (3) ta được:
x = 3.1/(5.1 - 2) = 1
Vậy S = {(1; 1)}





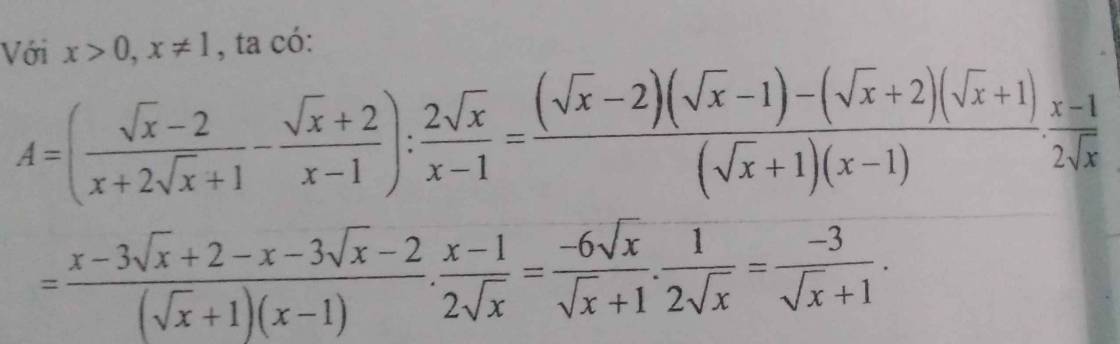



tính delta trước nha bạn
Tại sao vậy ạ?