Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình giải thích từ dấu tương đương 2 nha.
\(\dfrac{2x\left(x-2\right)+2x}{2x\left(x-1\right)\left(x-2\right)}=\dfrac{3\left(x-1\right)\left(x-2\right)}{2x\left(x-1\right)\left(x-2\right)}\)
\(\Leftrightarrow\dfrac{2x^2-4x+2x}{2x\left(x-1\right)\left(x-2\right)}-\dfrac{3\left(x-1\right)\left(x-2\right)}{2x\left(x-1\right)\left(x-2\right)}=0\)
\(\Leftrightarrow\dfrac{2x^2-2x-3\left(x^2-2x-x+2\right)}{2x\left(x-1\right)\left(x-2\right)}=0\)
Tới đây phải khử mẫu pt bằng cách lấy mẫu \(2x\left(x-1\right)\left(x-2\right)\) nhân với 0 bên vế phải thì pt mới đơn giản để giải tiếp được.
\(\Leftrightarrow2x^2-2x-3x^2+6x+3x-6=0\)
\(\Leftrightarrow2x^2-2x=3x^2-9x+6\)
Tới đây là ra được dấu tương đương 3 rồi đó.


gọi (a+b)=x,c=y
=>\(\left[\left(a+b\right)+c\right]^2=\left(x+y\right)^2\ge4xy=4\left(a+b\right)c\)
cái của bạn hơi sai sai phải là (b+c)4(b+c).a\(\ge\)16abc
dấu bằng xảy ra khi b=c=\(\dfrac{a}{2}\)

b: kẻ đường kính AD
góc ACD=90 độ=góc ABD
=>AC vuông góc CD và AB vuông góc BD
=>BH//CD và CH//BD
=>BDCH là hbh
=>H,N,D thẳng hàng và N là trung điểm của HD
=>NT là đường trung bình của ΔAHD
=>NT//AD và NT=1/2AD=OA
=>NT//OA
=>ATNO là hbh
EN=1/2BC
=>EN=BN
=>ΔNEB cân tại N
=>góc NBE=góc NEB
EJ=1/2AH=JH
=>ΔJEH cân tại J
=>góc JEH=góc JHE
góc NBE+Góc ACB=90 độ
góc HAC+góc ACB=90 độ
=>góc NBE=góc HAC
mà góc JHE+góc HAC=90 độ
nên góc JHE+góc NBE=90 độ
=>góc JEN=90 độ

cái này áp dụng hệ thức lượng thôi bạn
AH=căn 6^2-4,8^2=3,6cm
=>AC=6^2/3,6=10cm

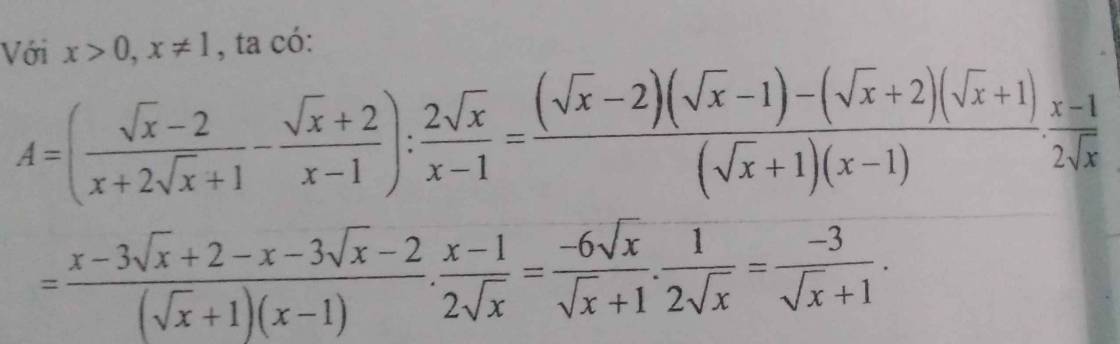








\(A=\left(\dfrac{\sqrt{x}-2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}+2}{x-1}\right):\dfrac{2\sqrt{x}}{x-1}\)
\(=\left(\dfrac{\sqrt{x}-2}{\sqrt{x}^2+2\sqrt{x}+1^2}-\dfrac{\sqrt{x}+2}{\sqrt{x}^2-1^2}\right).\dfrac{x-1}{2\sqrt{x}}\)
\(=\left(\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right).\dfrac{x-1}{2\sqrt{x}}\)
Tới đây là có được mẫu chung ở dấu = thứ 2 rồi.
\(A=\left(\dfrac{\sqrt{x}-2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}+2}{x-1}\right):\dfrac{2\sqrt{x}}{x-1}\) ( với x>0;\(x\ne1\) )
\(=\left[\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right].\dfrac{x-1}{2\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(x-1\right)}.\dfrac{x-1}{2\sqrt{x}}\)
\(=.....\) ( theo như trên )