
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)


Bài 3:
1, Áp dụng t/c dtsbn:
\(\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{3}=\dfrac{z-x}{3-6}=\dfrac{-21}{-3}=7\\ \Rightarrow\left\{{}\begin{matrix}x=42\\y=28\\z=21\end{matrix}\right.\)
2, Áp dụng t/c dtsbn:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}=\dfrac{2x+3y-z}{6+15-7}=\dfrac{-14}{14}=-1\\ \Rightarrow\left\{{}\begin{matrix}x=-3\\y=-5\\z=-7\end{matrix}\right.\)
Bài 4:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{4}}=\dfrac{x+y+z}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}}=\dfrac{130}{\dfrac{13}{12}}=120\)
Do đó: x=60; y=40; z=30


Câu 3:
a) \(MG=\dfrac{2}{3}ME\)
b) MG=2GE
Câu 5: C
Câu 6: B

a) Các điểm có hoành độ bằng 2021 là các điểm thuộc đường thẳng song song với trục tung và cắt trục hoành tại điểm có hoành độ bằng 2021.
b) Các điểm có tung độ bằng -2022 là các điểm thuộc đường thẳng y = -2022
c) Các điểm có tung độ bằng hoành độ là các điểm thuộc đường thẳng y = x
d) Các điểm có tung độ và hoành độ đối nhau là các điểm thuộc đường thẳng y = -x.
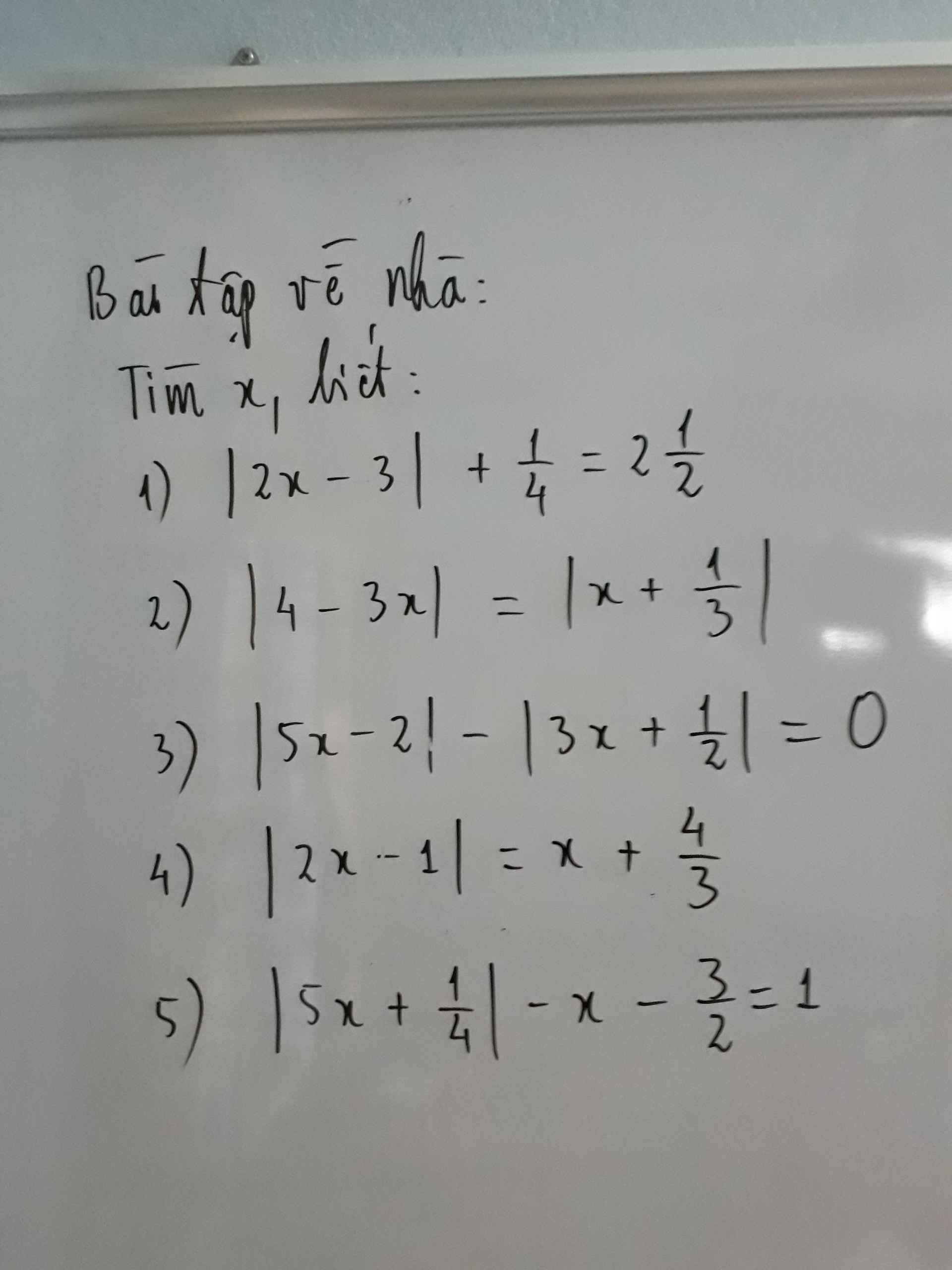



 lm giúp mk bài 3 với bài 4 với ạ, mk đng cần gấp, cảm ơn mn rất rất nhiều ạ !!!!
lm giúp mk bài 3 với bài 4 với ạ, mk đng cần gấp, cảm ơn mn rất rất nhiều ạ !!!!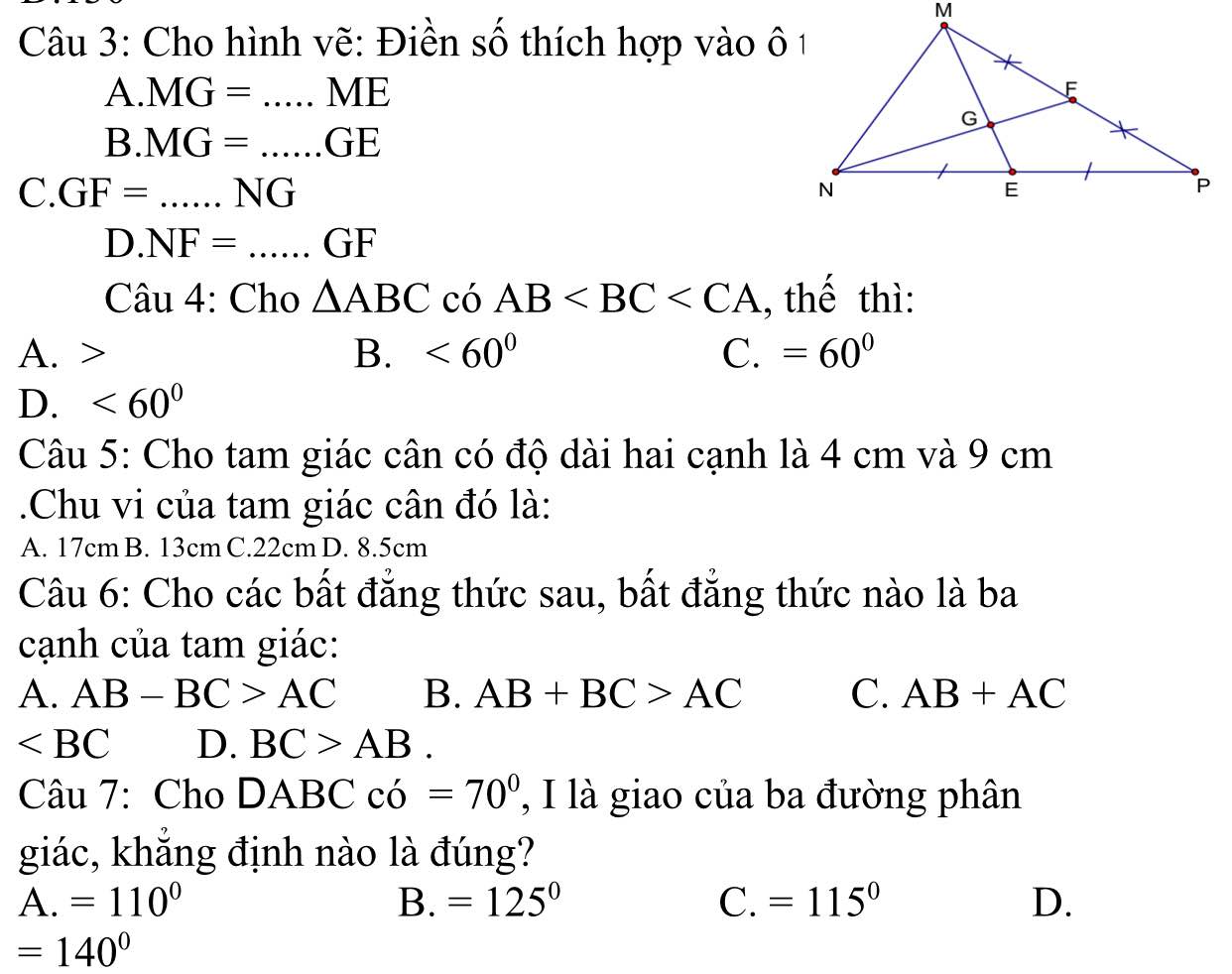

2) Ta có: \(\left|4-3x\right|=\left|x+\dfrac{1}{3}\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}4-3x=x+\dfrac{1}{3}\\3x-4=x+\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-4x=-\dfrac{11}{3}\\2x=\dfrac{13}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11}{12}\\x=\dfrac{13}{6}\end{matrix}\right.\)
3: Ta có: \(\left|5x-2\right|-\left|3x+\dfrac{1}{2}\right|=0\)
\(\Leftrightarrow\left|5x-2\right|=\left|3x+\dfrac{1}{2}\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-2=3x+\dfrac{1}{2}\\5x-2=-3x-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{5}{2}\\8x=\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{4}\\x=\dfrac{3}{16}\end{matrix}\right.\)
4: Ta có: \(\left|2x-1\right|=x+\dfrac{4}{3}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=x+\dfrac{4}{3}\left(x\ge\dfrac{1}{2}\right)\\1-2x=x+\dfrac{4}{3}\left(x< \dfrac{1}{2}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x-x=\dfrac{4}{3}+1\\-2x-x=\dfrac{4}{3}-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{3}\\-3x=\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{3}\\x=-\dfrac{1}{9}\end{matrix}\right.\)
Làm giúp mik câu 5 với ạ