
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó; ΔABM=ΔACM
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: AE=AF và ME=MF
hay ΔMEF cân tại M
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC

a.Xét tam giác vuông AED và tam giác vuông AFD, có:
A: góc chung
AD: cạnh chung
Vậy tam giác vuông AED = tam giác vuông AFD ( cạnh huyền . góc nhọn)
=> DE = DF ( 2 cạnh tương ứng )
b.Xét tam giác vuông BDE và tam giác vuông CDF, có:
góc B = góc C ( gt )
DE = DF ( cmt )
Vậy tam giác vuông BDE = tam giác vuông CDF ( góc nhọn. cạnh góc vuông )
c. ta có: AD là đường phân giác trong tam giác cân ABC cũng là đường trung trực
=> AD là đường trung trực của BC
Chúc bạn học tốt!!!

a: Ta có: ΔABC cân tại A
mà AM là đường cao
nên AM vừa là đường trung tuyến vừa là đường phân giác
=>MB=MC và \(\widehat{MAB}=\widehat{MAC}\)
b: BC=16cm
=>BM=8cm
=>AM=6cm
c: Xét ΔEAM vuông tạiE và ΔFAM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó:ΔEAM=ΔFAM
Suy ra: AE=AF
d: Xét ΔABC có AE/AB=AF/AC
nên EF//BC

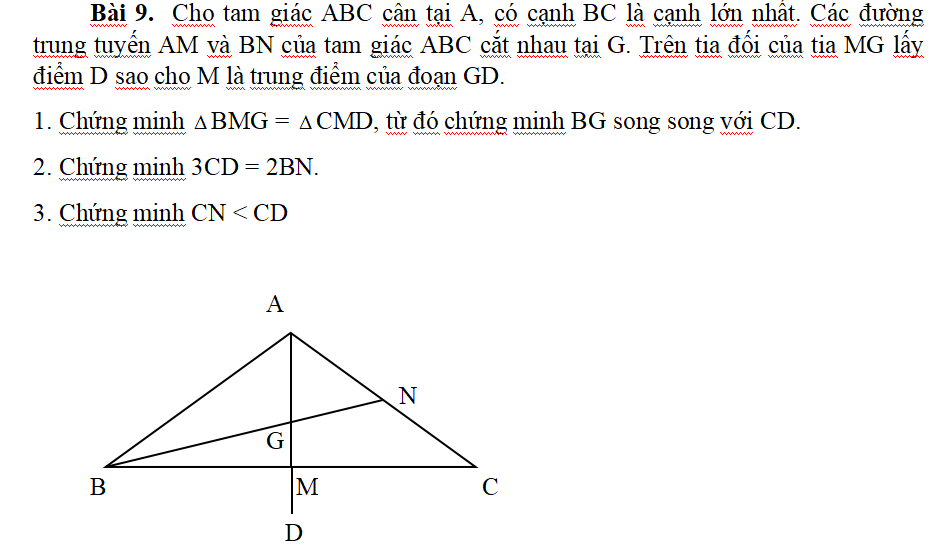
1: Xét ΔBMG và ΔCMD có
MB=MC
\(\widehat{BMG}=\widehat{CMD}\)
MG=MD
Do đó: ΔBMG=ΔCMD
Xét tứ giác BGCD có
M là trung điểm của BC
M là trung điểm của GD
Do đó: BGCD là hình bình hành
Suy ra: BG//CD
2: Xét ΔBAC có
AM là đường trung tuyến
BN là đường trung tuyến
AM cắt BN tại G
Do đó: G là trọng tâm
=>BG=2/3BN
=>BG=2/3DC
hay 3CD=2BN

a) Góc xAK kề bù với góc 115 độ nên góc xAK = 650
Vì Ky song song với Ax nên góc AKy = xAk = 650 ( so le trong )
b) Vì Ky song song với Mz nên zMK + yKM = 1800 ( trong cùng phía ) => góc yKM = 350
=> góc AKM = AKy + yKM = 550 + 350 = 900 hay AK vuông góc với MK

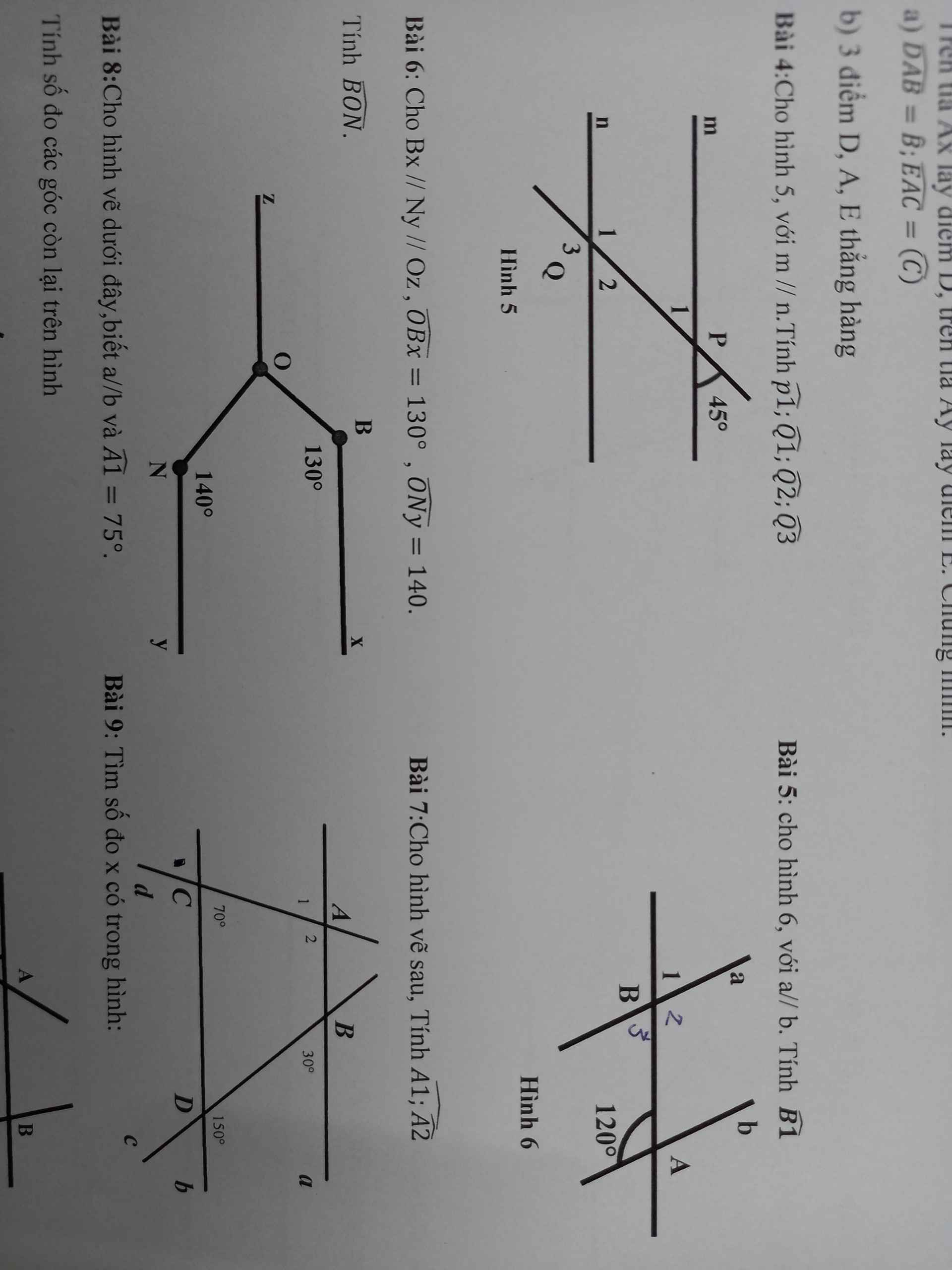
bài 5
góc BAb=1800-1200=600
mà B1=góc BAb=600(so le trong)
bài 7
có góc BDC=1800- góc BDb=1800-1500=300
=>góc BDC= góc aBD
=>a//b
=>A1=góc ACD=700
=>A2=1800-ACD=1800-700=1100

Ta có: \(ab=6\)
\(\Rightarrow2ab=12\)
\(\Rightarrow a^2+b^2+2ab=a^2+b^2+12\)
\(\Rightarrow a^2+b^2+2ab=13+12=25\)
\(\Rightarrow\left(a+b\right)^2=5^2\)
\(\Rightarrow a+b=5\) hoặc \(a+b=-5\)
\(\Rightarrow\left|a+b\right|=5\)
Vậy \(\left|a+b\right|=5.\)
 Mn giải hộ mk vs.
Mn giải hộ mk vs.



Bài 13:
Số tiền lãi sau 6 tháng là:
2 062 400 - 2 000 000 = 62 400 (đồng)
Số tiền lãi hằng tháng là:
62 400 : 6 = 10 400 (đồng)
Bài 14:
Gọi số tiền lãi của tổ 1 là a
số tiền lãi của tổ 2 là b
Ta có: \(\frac{a}{3}=\frac{b}{5}\) và \(a+b=12800000\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{3}=\frac{b}{5}=\frac{a+b}{3+5}=\frac{12800000}{8}=1600000\)
\(\frac{a}{3}=1600000\Rightarrow a=1600000\times3=4800000\)
\(\frac{b}{5}=1600000\Rightarrow b=1600000\times5=8000000\)
Vậy tổ 1 nhận được 4 800 000 đồng tiền lãi
tổ 2 nhận được 8 000 000 đồng tiền lãi
Chúc bạn học tốt
2 062 400 - 2 000 000 = 62 400 (đồng)
Số tiền lãi hằng tháng là:
62 400 : 6 = 10 400 (đồng)
Bài 14:
Gọi số tiền lãi của tổ 1 là a
số tiền lãi của tổ 2 là b
Ta có: a3=b5a3=b5 và a+b=12800000a+b=12800000
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
a3=b5=a+b3+5=128000008=1600000a3=b5=a+b3+5=128000008=1600000
a3=1600000⇒a=1600000×3=4800000a3=1600000⇒a=1600000×3=4800000
b5=1600000⇒b=1600000×5=8000000b5=1600000⇒b=1600000×5=8000000
Vậy tổ 1 nhận được 4 800 000 đồng tiền lãi
tổ 2 nhận được 8 000 000 đồng tiền lãi
Chúc bạn học tốt