
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a - b = a : b = 2( a + b ) (1)
Xét a - b = 2( a + b )
⇔ a - b = 2a + 2b
⇔ a - b - 2a - 2b = 0
⇔ -a - 3b = 0
⇔ -a = 3b
⇔ a = -3b
Thế a = -3b vào (1) ta có :
-3b - b = -3b : b = 2( -3b + b )
⇔ -4b = -3
⇔ b = 3/4
a = -3b ⇔ a = -3.3/4 = -9/4
Vậy a = -9/4 ; b = 3/4


Có\(\left|x-2010\right|+\left|x-2012\right|+\left|x-2014\right|\ge\left|x-2010+2014-x\right|+\left|x-2012\right|\ge2\)
mà\(\left|x-2010\right|+\left|x-2012\right|+\left|x-2014\right|=2\)
dấu "=' \(\Leftrightarrow\left\{{}\begin{matrix}x-2012=0\\2010\le x\le2014\end{matrix}\right.\)\(\Rightarrow x=2012\)

a: Xét ΔABD và ΔACD có
AB=AC
BD=CD
AD chung
Do đó: ΔABD=ΔACD
b: ΔABD=ΔACD
=>\(\widehat{ADB}=\widehat{ADC}\)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
c: Ta có: \(\widehat{ADB}=90^0\)
=>AD\(\perp\)BC tại D
D là trung điểm của BC
=>\(DB=DC=\dfrac{BC}{2}=\dfrac{24}{2}=12\left(cm\right)\)
ΔADB vuông tại D
=>\(AD^2+DB^2=AB^2\)
=>\(AD^2=20^2-12^2=256\)
=>\(AD=\sqrt{256}=16\left(cm\right)\)
Xét ΔABC có
AD là đường trung tuyến
G là trọng tâm
Do đó: \(AG=\dfrac{2}{3}AD=\dfrac{2}{3}\cdot16=\dfrac{32}{3}\left(cm\right)\)
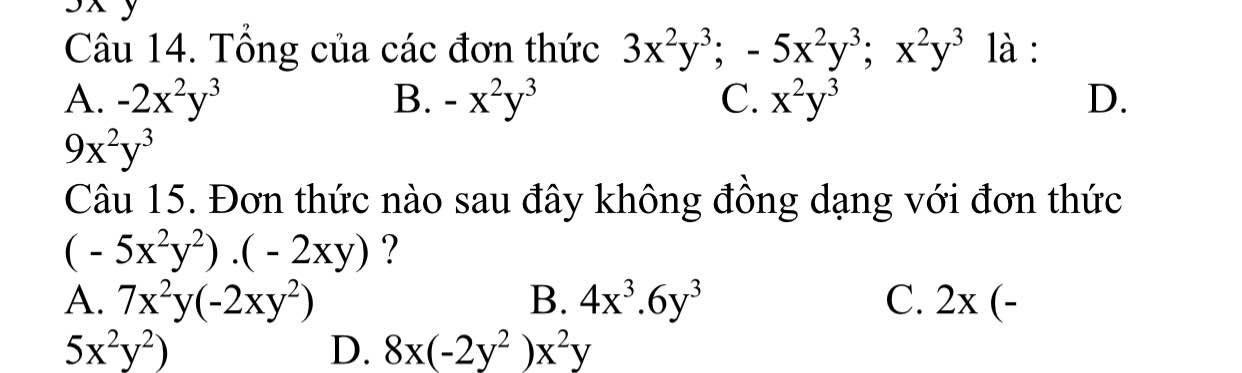

 giúp mk với, mk cần gấp ạ. camon mn rất nhìu, giải chi tiết dễ hiểu giúp mk nha
giúp mk với, mk cần gấp ạ. camon mn rất nhìu, giải chi tiết dễ hiểu giúp mk nha
Ta có: \(ab=6\)
\(\Rightarrow2ab=12\)
\(\Rightarrow a^2+b^2+2ab=a^2+b^2+12\)
\(\Rightarrow a^2+b^2+2ab=13+12=25\)
\(\Rightarrow\left(a+b\right)^2=5^2\)
\(\Rightarrow a+b=5\) hoặc \(a+b=-5\)
\(\Rightarrow\left|a+b\right|=5\)
Vậy \(\left|a+b\right|=5.\)
Bài giải hay