2D
Mn giải giúp mình với mình cần gấp lắm hôm nay mình pgair nộp rồi
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
YN
2
H
28 tháng 4 2022
1)
a. Xét tg ABC cân tại A có AC=AB; gACB = g ABC.
Xét tg ACN và tg ABM có:
CN=BM (gt)
AC=AB
gACB=gABC
=> tg ACN = tg ABM (cgc)
=> AN=AM (2 cạnh tg ứng)
H là trung điểm BC nên AH là đường trung tuyến của tg ABC
Mak tg ABC cân => H cũng là đường cao của tg ABC => AH ⊥ BC
b. Vì H là trung đ của BC nên CH=HB=BC/2= 3cm
Áp dụng định lý Py ta go vào tg AHB có:
AB^2=AH^2+HB^2
AH^2= AB^2 - HB^2
AH^2= 5^2 - 3^2 = 16 cm
=> AH= 4 cm
c. Xét tg AMN và tg KMB có:
AM=KM (gt)
MN=BM (gt)
gHMA=gKMB (đối đỉnh)
=> tg AMN = tg KMB (cgc)
d. tg AMN = tg KMB => gMAN=gMKB
=> AN=KB=Am
Mà AB>AM (quan hệ giữ đường xiêng và hình chiếu) nên AB>BK
=> gBKA> gBAK
=> gMAN>gBAM
20 tháng 8 2021
Bài 1:
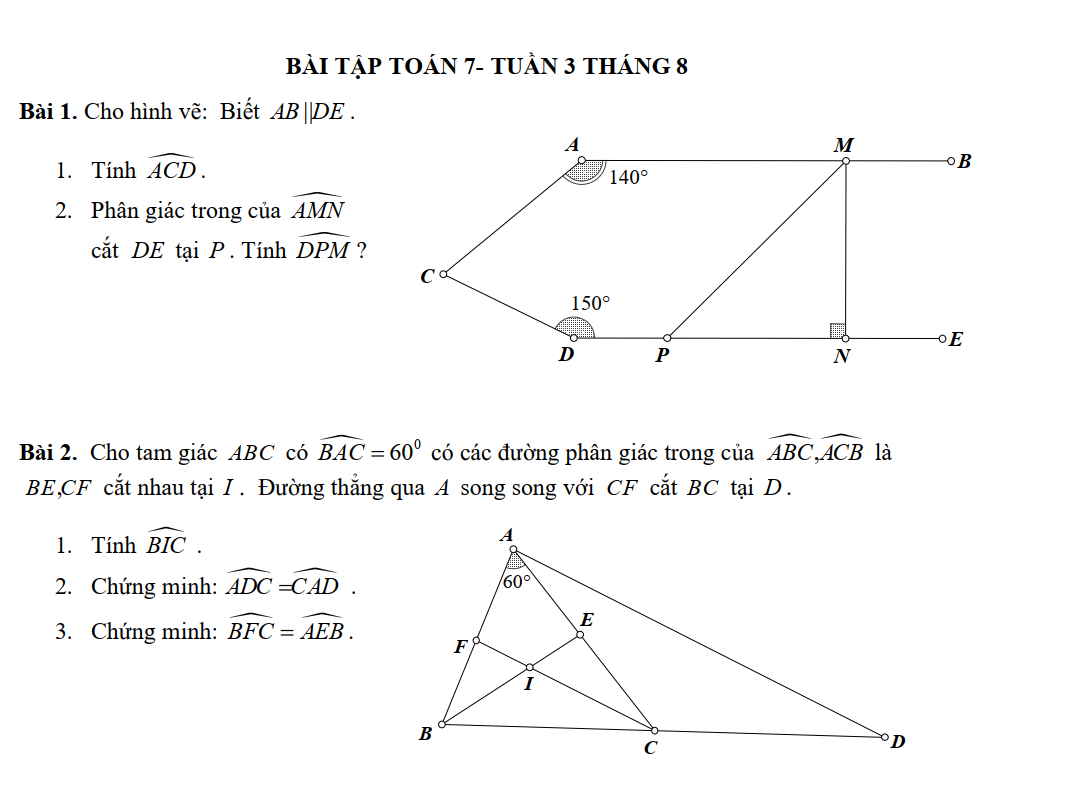
1) Kẻ tia Cx//AB//DE
Ta có: Cx//AB
\(\Rightarrow\widehat{BAC}+\widehat{ACx}=180^0\)(2 góc trong cùng phía)
\(\Rightarrow\widehat{ACx}=180^0-\widehat{BAC}=180^0-140^0=40^0\)
Ta có: Cx//DE
\(\Rightarrow\widehat{xCD}+\widehat{CDE}=180^0\)( 2 góc trong cùng phía)
\(\Rightarrow\widehat{xCD}=180^0-\widehat{CDE}=180^0-150^0=30^0\)
\(\Rightarrow\widehat{ACD}=\widehat{ACx}+\widehat{xCD}=40^0+30^0=70^0\)
2) Ta có AB//DE(gt)
Mà DE⊥MN
=> AB⊥MN =>\(\widehat{AMN}=90^0\Rightarrow\dfrac{1}{2}\widehat{AMN}=45^0\Rightarrow\widehat{AMP}=45^0\) (do MP là tia phân giác \(\widehat{AMN}\))
Ta có AB//DE
=> \(\widehat{AMP}+\widehat{DPM}=180^0\) (2 góc trong cùng phía)
\(\Rightarrow\widehat{DPM}=180^0-\widehat{AMP}=180^0-45^0=135^0\)
2D
1
15 tháng 10 2021
Bài 2:
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{45}{9}=5\)
Do đó: a=10; b=15;c=20
8 tháng 11 2019
\(B=|2014-2x|+|2016-2x|\)
\(=|2014-2x|+|2x-2016|\ge|2014-2x+2x-2016|\)
Hay \(B\ge2\)
Dấu"="xảy ra \(\Leftrightarrow\left(2014-2x\right)\left(2x-2016\right)\ge0\)
\(\Leftrightarrow\hept{\begin{cases}2014-2x\ge0\\2x-2016\ge0\end{cases}}\)hoặc \(\hept{\begin{cases}2014-2x< 0\\2x-2016< 0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x\le2014\\2x\ge2016\end{cases}\left(loai\right)}\)hoặc\(\hept{\begin{cases}2x>2014\\2x< 2016\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x>1007\\x< 1008\end{cases}}\)
\(\Leftrightarrow1007< x< 1008\)
Vậy \(B_{min}=2\)\(\Leftrightarrow1007< x< 1008\)
2H
0
30 tháng 8 2021
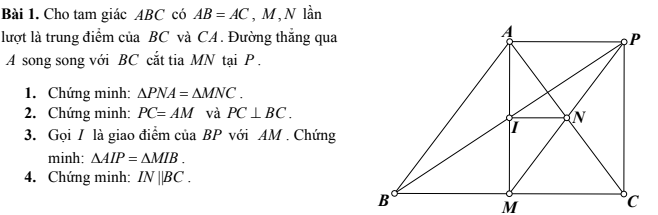
4: Xét ΔAMC có
I là trung điểm của AM
N là trung điểm của AC
Do đó: IN là đường trung bình của ΔAMC
Suy ra: IN//MC
hay IN//BC
31 tháng 8 2021
1: Xét ΔABC có AB=AC
nên ΔABC cân tại A
Suy ra: \(\widehat{B}=\widehat{C}\)
Ta có: ΔBAC cân tại A
mà AH là đường trung tuyến ứng với cạnh đáy BC
nên AH là đường cao ứng với cạnh BC
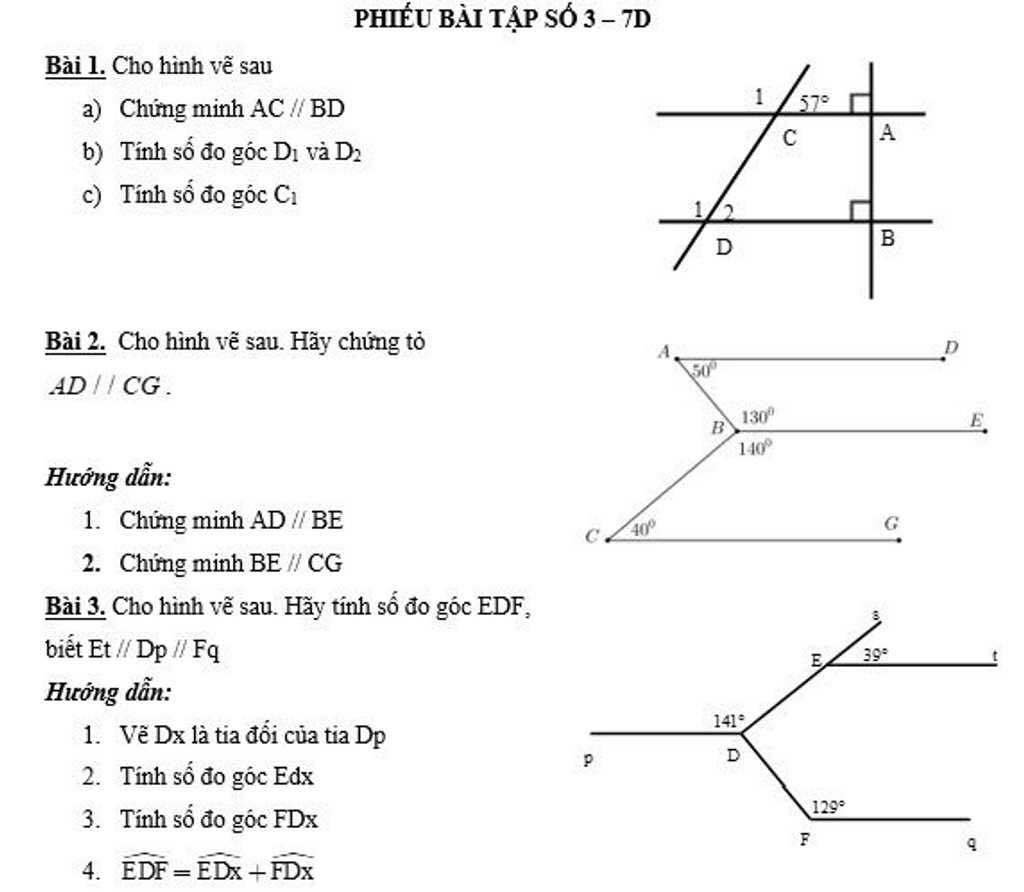
\(1,\\ a,\left\{{}\begin{matrix}AC\perp AB\\BD\perp AB\end{matrix}\right.\Rightarrow AC//BD\\ b,AC//BD\Rightarrow\widehat{D_2}=\widehat{C_1}=57^0\left(đồng.vị\right)\\ \widehat{D_2}+\widehat{D_1}=180^0\left(kề.bù\right)\Rightarrow\widehat{D_1}=180^0-57^0=123^0\\ c,AC//BD\Rightarrow\widehat{D_1}=\widehat{C_1}=123^0\left(đồng.vị\right)\)
\(2,\\ \widehat{DAB}+\widehat{ABE}=50^0+130^0=180^0\)
Mà 2 góc này ở vị trí TCP nên AD//BE (1)
\(\widehat{EBC}+\widehat{BCG}=140^0+40^0=180^0\)
Mà 2 góc này ở vị trí TCP nên BE//CG (2)
Từ (1)(2) ta được AD//CG