Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi A, B lần lượt là tập hợp các học sinh thích môn Toán và Tiếng Anh, X là tập hợp học sinh lớp 10H.
Theo giả thiết, \(n(A) = 20,n(B) = 16,n(A \cap B) = 12,n(X) = 35\)

a) Nhận thấy rằng, nếu tính tổng \(n(A) + n(B)\) thì ta được số học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh, nhưng số học sinh thích cả hai môn Toán và Tiếng Anh được tính hai lần. Do đó, số học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh là:
\(n(A \cup B) = n(A) + n(B) - n(A \cap B) = 20 + 16 - 12 = 24\)
b) Trong số 35 học sinh lớp 10H, có 24 học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh, còn lại số học sinh không thích cả hai môn này là: \(35 - 24 = 11\) (học sinh).

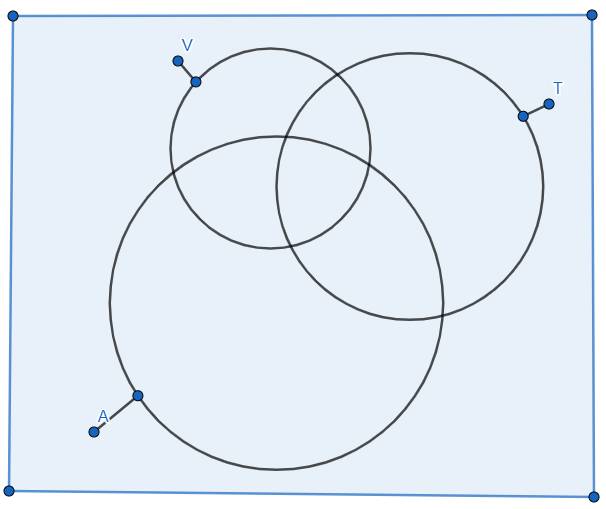
Gọi V, T, A lần lượt là tập hợp các học sinh giỏi Văn, Toán, Tiếng Anh. Theo đề bài, ta có: \(\left|V\right|=18;\left|T\right|=20;\left|A\right|=22\)\(;\left|V\cap T\cap A\right|=5\)\(;\left|A\cup T\cup V\right|=34\)
Áp dụng công thức bù trừ, ta có:
\(\left|V\cup T\cup A\right|=\left|V\right|+\left|T\right|+\left|A\right|-\left|V\cap T\right|-\left|T\cap A\right|-\left|A\cap V\right|+\left|V\cap T\cap A\right|\)
\(\Rightarrow34=18+20+22-P+5\) (với \(P=\left|V\cap T\right|+\left|T\cap A\right|+\left|A\cap V\right|\))
\(\Rightarrow P=31\)
Số học sinh thích đúng 1 môn trong 3 môn Toán, Văn, Tiếng Anh chính bằng:
\(\left|V\cup T\cup A\right|-P+2\left|V\cap T\cap A\right|\) \(=34-31+2.5=13\) (học sinh)

Gọi x, y, z lần lượt là số học sinh đạt loại giỏi một môn, hai môn và ba môn. Lập sơ đồ Ven liên hệ giữa các tập hợp, ta có hệ phương trình:
x + y + z = 45 − 7 x + 2 y + 3 z = 20 + 18 + 17 z = 5 ⇔ x = 26 y = 7 z = 5.
Vậy số học sinh đạt loại giỏi một môn là 26 em.
Đáp án B

Gọi A,B,C là tập hợp các học sinh tích môn toán , Văn , Anh
ta có :
\(\hept{\begin{cases}\left|A\right|=10,\left|B\right|=20,\left|C\right|=25\\\left|A\cap B\cap C\right|=3\\\left|A\cup B\cup C\right|=40\end{cases}}\) ta có : \(\left|A\cup B\cup C\right|=\left|A\right|+\left|B\right|+\left|C\right|-\left(\left|A\cap B\right|+\left|B\cap C\right|+\left|C\cap A\right|\right)+\left|A\cap B\cap C\right|\)
nên \(\left|A\cap B\right|+\left|B\cap C\right|+\left|C\cap A\right|=18\)
Do đó số học sinh chỉ thích đúng hai môn là :
\(\left|A\cap B\right|+\left|B\cap C\right|+\left|C\cap A\right|-3\left|A\cap B\cap C\right|=18-3\times3=9\)

Gọi tập hợp các "đồng chí" nói đc tiếng Anh là A, tiếng Pháp là B
Số "đồng chí" chỉ nói được ít nhất một thứ tiếng bằng: \(100-23=77\)(bạn)
Số "đồng chí" chỉ nói đc tiếng Anh bằng: \(A/B=70-23=47\)(bạn)
Số "đồng chí" chỉ nói đc tiếng Pháp bằng: \(B/A=45-23=22\)(bạn)
Suy ra số "đồng chí" "mù" tiếng (:>) bằng: \(77-47-22=8\)(bạn)
Thế thôi, chúc bạn học tốt nha![]() .
.
Cách giải của bạn Lâm là đúng rồi. Nhưng có thể sẽ có nhiều b đọc thắc mắc vì sao 70 trừ 23 rồi mà 45 vẫn trừ 23. Đó là bởi vì 23 hs nói đc 2 thứ tiếng được kể lặp lại 2 lần. Ở nhóm hs chỉ nói Anh thì cũng tính 23 hs nói đc Anh+Pháp, mà ở nhóm hs chỉ nói Pháp thì cũng tính 23 hs này.
Bài toán được diễn giải rất dễ hiểu như sau.
Lớp học 100 hs đc chia làm 3 nhóm: ko nói đc tiếng - nói đc 1 thứ tiếng hoặc A hoặc P - nói đc cả 2 thứ tiếng A và P. Trong đó đã xd đc có 23 hs nói dc 2 thứ tiếng. Như vậy tổng số hs mù tiếng và chỉ nói đc 1 tiếng là 100 - 23 = 77 hs.
Phân tích dữ liệu t2:
Trong Nhóm 70 hs nói tiếng Anh thì đã có 23 hs nói đc cả A lẫn P => 70 - 23 = 47 hs chỉ nói đc 1 thứ tiếng Anh.
Tương tự ở nhóm 45 hs nói tiếng P thì đã có 23 hs nói đc cả A lẫn P => 45 - 23 = 22 hs chỉ nói đc 1 thứ tiếng Pháp.
(Phần này có thể đc thu gọn bằng phép tính chung: (70+45) - 23×2 = 69
Hay 47 + 22 = 69. 69 em hs này là những hs chỉ nói đc 1 thứ tiếng hoặc Anh hoặc Pháp.
Quay lại dữ liệu ban đầu, ta có tổng số hs mù tiếng và số hs chỉ nói đc 1 thứ tiếng (hoặc A hoặc P) là 77 em. Trong đó 69 em chỉ nói đc 1 thứ tiếng.
Vậy số hs mù tiếng là: 77 - 69 = 8 (hs).
Mấu chốt ở những bài toán này là mẹo dựa trên sự giống nhau trong dữ liệu đề cho. Chính vì vậy bắt tay vào làm càng tách bạch càng tốt. Ở bài này, trong tập thể 100 em, cần chia ra 3 loại hs tiêu biểu nhất (tránh chia thành 4 loại: cả 2 tiếng - chỉ tiếng Anh - chỉ tiếng P - mù tiếng sẽ gây rối thêm) sao cho chính xác và phù hợp với đề bài. Đồng thời suy nghĩ nhiều lần trc khi tính toán để tránh bị mắc bẫy. Ở bài toán này ko ít người chất vấn phép tính (70 + 45) - 23×2 nếu ko đc giải thích rõ vì các b hiểu theo kiểu: 23 hs nói cả 2 thứ tiếng bị chia 1 ít vào nhóm 70 Anh và 1 ít còn lại vào nhóm 45 Pháp. Thành ra khi làm sẽ tính như sau: (70 anh +45 pháp ) - 23 anh và pháp= 92 hs chỉ nói 1 thứ tiếng hoặc anh hoặc pháp. Sau đó nhận ra 92 > 77 => ko lẽ số hs mù tiếng là âm? Thành ra bị bí bách. Thực tế là vì 23 hs này đều nói đc cả 2 thứ tiếng nên nhóm 70 Anh cũng có 23 em này và nhóm 45 Pháp cũng có 23 em này.

Tổng số học sinh giỏi là: 45 – 13 = 32
Số học sinh chỉ giỏi Văn là: 32 – 25 = 7
Số học sinh chỉ giỏi Toán là: 32 – 17 =15
Số học sinh giỏi cả hai môn là: 32 – 7 – 15 = 10.
Lớp 10A có số học sinh là:
\(30+20+15-\left(3+4+2\right)=56\) (bạn)
Có thể giải bài toán cụ thể hơn như sau: Trong hình vẽ sau, hình tròn tâm A biểu diễn tập hợp các học sinh học tiếng Anh; hình tròn tâm B biểu diễn tập hợp các học sinh học tiếng Pháp và hình tròn tâm C biểu diễn tập hợp các học sinh học tiếng Trung. Ta cũng dùng kí hiệu \(\left|A\right|\) để chỉ số phần tử của tập hợp A. Như vậy giả thiết của bài toán cho \(\left|A\right|=30;\left|B\right|=20;\left|C\right|=15;\left|A\cap B\cap C\right|=0;\left|A\cap B\backslash C\right|=\left|A\cap B\right|=2;\)
\(\left|B\cap C\backslash A\right|=\left|B\cap C\right|=4;\left|C\cap A\backslash B\right|=\left|C\cap A\right|=3\).
Từ đó số học sinh của lớp là \(30+20+15-\left(2+4+3\right)=56\)