Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số học sinh chỉ giỏi Toán là:
20-10=10(bạn)
Số học sinh chỉ giỏi Lý là:
20-10=10(bạn)
Số học sinh chỉ giỏi Hóa là:
45-10-10=25(bạn)

Gọi \(X\) là tập hợp các học sinh trong lớp, \(A,B\) lần lượt là tập hợp các học sinh đăng kí chơi cầu lông và chơi bóng bàn.
Như vậy tập hợp học sinh đăng kí chơi cả hai môn là \(A\cap B\). Tập hợp học sinh đăng kí ít nhất một môn là \(A\cup B\)
Ta có \(N\left(A\cup B\right)=50-10=40\)
\(a,\) Ta có \(N\left(A\cup B\right)=N\left(A\right)+N\left(B\right)-N\left(A\cap B\right)\)
\(\Rightarrow N\left(A\cap B\right)=\left(A\right)+N\left(B\right)-N\left(A\cup B\right)=30+28-40=18\)
Vậy có \(18\) học sinh đăng kí chơi cả hai môn
\(b,\) Số học sinh chỉ đăng kí chơi một môn là
\(N\left(A\cup B\right)-N\left(A\cap B\right)=40-18=22\)

Số học sinh chỉ giỏi Toán và Hóa nhưng không giỏi Lý là:
3-1=2(bạn)
Số học sinh chỉ giỏi Toán và Lý nhưng không giỏi Hóa là:
4-1=3(bạn)
Số học sinh chỉ giỏi Lý và Hóa nhưng không giỏi Toán là:
2-1=1(bạn)
Số học sinh chỉ giỏi Toán nhưng không giỏi Lý và Hóa là:
15-2-3-1=9(bạn)
Số học sinh chỉ giỏi Lý nhưng không giỏi Toán và Hóa là:
12-3-1-1=7(bạn)
Số học sinh chỉ giỏi Hóa nhưng không giỏi Toán và Lý là:
10-2-1-1=10-4=6(bạn)
Số học sinh của lớp 10A giỏi ít nhất 1 môn là:
2+3+1+9+7+6+1=29(bạn)

Đáp án A
Theo giả thiết đề bài cho, ta có biểu đồ Ven:
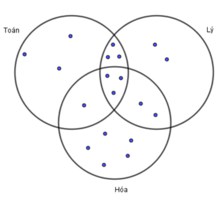
Dựa vào biểu đồ Ven ta thấy:
Số học sinh chỉ giỏi Toán và Lý (không giỏi Hóa) là: 6−3=3 (em)
Số học sinh chỉ giỏi Toán và Hóa (không giỏi Lý) là: 4−3=1 (em)
Số học sinh chỉ giỏi Lý và Hóa (không giỏi Toán) là: 5−3=2 (em)
Số học sinh chỉ giỏi một môn Toán là: 10−3−3−1=3 (em)
Số học sinh chỉ giỏi một môn Lý là: 10−3−3−2=2 (em)
Số học sinh chỉ giỏi một môn Hóa là: 11−1−3−2=5 (em)
Số học sinh giỏi ít nhất một trong ba môn là:
3+2+5+1+2+3+3=19 (em)

\(\left\{{}\begin{matrix}16:hsg.Toán\\15:hsg.Lý\\11:hsg.Hóa\end{matrix}\right.\) và \(9:hsg.đúng.2.môn\)
Số học sinh giỏi cả 3 môn Toán, Lý, Hóa:
\(11-9=2\) (học sinh)
Số học sinh giỏi đúng 1 môn Toán, Lý hoặc Hóa:
\(16-15=1\)(học sinh)

Đáp án C
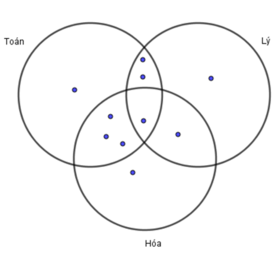
Số học sinh giỏi toán, lý mà không giỏi hóa: 3−1=2.
Số học sinh giỏi toán, hóa mà không giỏi lý: 4−1=3.
Số học sinh giỏi hóa, lý mà không giỏi toán: 2−1=1.
Số học sinh chỉ giỏi môn lý: 5−2−1−1=1.
Số học sinh chỉ giỏi môn hóa: 6−3−1−1=1.
Số học sinh chỉ giỏi môn toán: 7−3−2−1=1.
Số học sinh giỏi ít nhất một (môn toán, lý, hóa) là số học sinh giỏi 1 môn hoặc 2 môn hoặc cả 3 môn: 1+1+1+1+2+3+1=10.
bn ơi bn cho mik hỏi cái câu hỏi số hs......toán lý hóa cái câu ng ta hỏi đấy là như nào ạ mik đọc mik k hiểu lắm
 giúp em với ạ
giúp em với ạ
Câu 1C
Câu 2C
Em không hiểu thì cứ hỏi lại nha!
Dạ cảm ơn ạaa