K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 9 2021
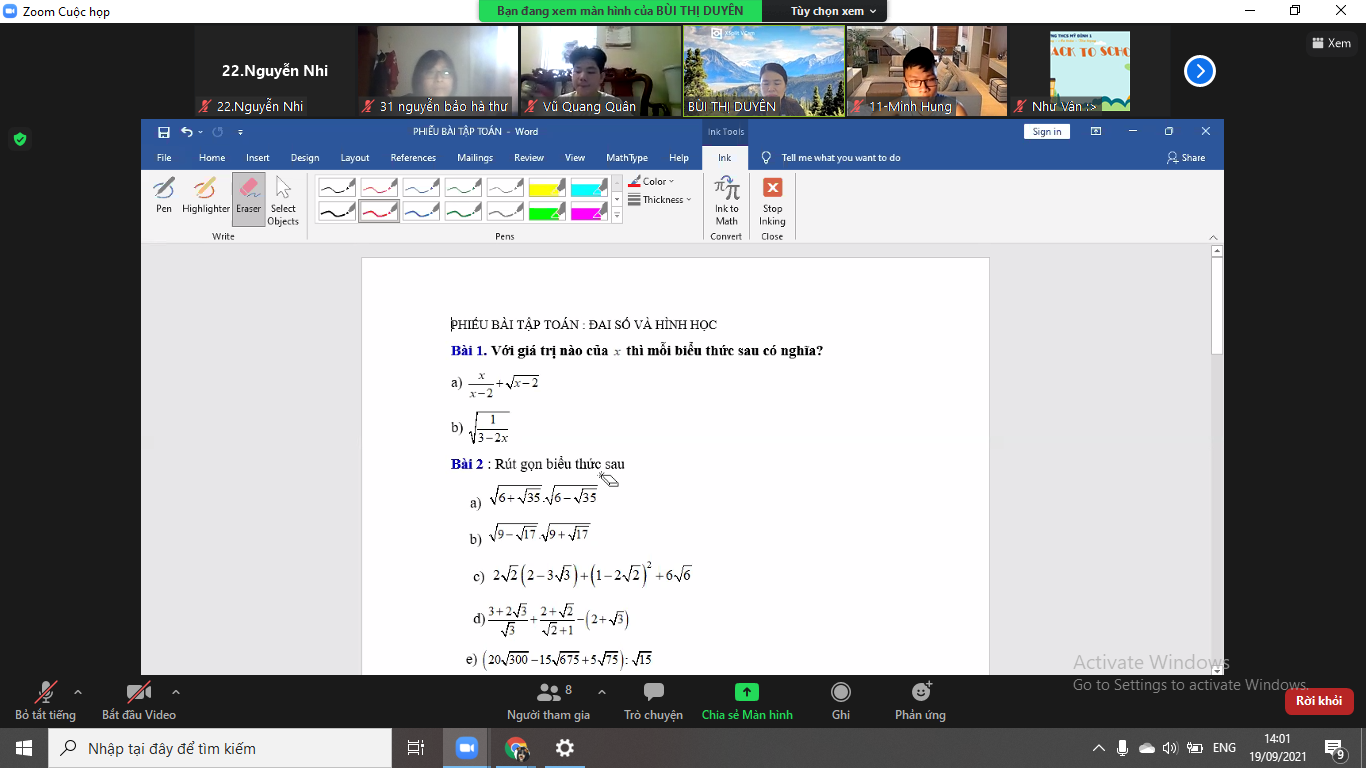
\(1,\\ a,ĐK:\left\{{}\begin{matrix}x-2\ne0\\x-2\ge0\end{matrix}\right.\Leftrightarrow x>2\\ b,ĐK:\dfrac{1}{3-2x}\ge0\Leftrightarrow3-2x\ge0\left(1>0\right)\Leftrightarrow x\le\dfrac{3}{2}\)
\(2,\\ a,=\sqrt{\left(6-\sqrt{35}\right)\left(6+\sqrt{35}\right)}=\sqrt{36-35}=\sqrt{1}=1\\ b,=\sqrt{\left(9-\sqrt{17}\right)\left(9+\sqrt{17}\right)}=\sqrt{81-17}=\sqrt{64}=8\\ c,=4\sqrt{2}-6\sqrt{6}+9-4\sqrt{2}+6\sqrt{6}=9\\ d,=\dfrac{\sqrt{3}\left(\sqrt{3}+2\right)}{\sqrt{3}}+\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt{2}+1}-2-\sqrt{3}=\sqrt{3}+\sqrt{2}-2-\sqrt{3}=\sqrt{2}-2\\ e,=\left(200\sqrt{3}-225\sqrt{3}+25\sqrt{3}\right):\sqrt{15}=0:\sqrt{15}=0\)
18 tháng 2 2021
1) Vì x=25 thỏa mãn ĐKXĐ nên Thay x=25 vào biểu thức \(A=\dfrac{\sqrt{x}-2}{x+1}\), ta được:
\(A=\dfrac{\sqrt{25}-2}{25+1}=\dfrac{5-2}{25+1}=\dfrac{3}{26}\)
Vậy: Khi x=25 thì \(A=\dfrac{3}{26}\)
2) Ta có: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}+\dfrac{2x+8\sqrt{x}-6}{x-\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-5\sqrt{x}+6+2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+3\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)
T
1
10 tháng 6 2021
Bài 1.2
\(A=\dfrac{2\sqrt{x}+7}{\sqrt{x}+2}=2+\dfrac{3}{\sqrt{x}+2}\)
C1:Bạn dùng pp chặn như bài 2.2
C2: (Gợi ý)\(\sqrt{x}+2\ge2\) và \(\sqrt{x}+2\inƯ\left(3\right)\)\(\Rightarrow\sqrt{x}+2=3\Leftrightarrow x=1\)
Vậy x=1 thì A nguyên
Bài 2.2
\(A=\dfrac{\sqrt{x}+7}{\sqrt{x}+2}=1+\dfrac{5}{\sqrt{x}+2}\)
Do \(\sqrt{x}\ge0;\forall x\)\(\Rightarrow\sqrt{x}+2\ge2\) \(\Rightarrow\dfrac{5}{\sqrt{x}+2}\le\dfrac{5}{2}\)\(\Rightarrow A\le\dfrac{7}{2}\) (1)
mà \(\dfrac{5}{\sqrt{x}+2}>0;\forall x\Rightarrow A>1\) (2)
Từ (1) (2) \(\Rightarrow1< A\le\dfrac{7}{2}\) mà A nguyên
\(\Rightarrow\left[{}\begin{matrix}A=2\\A=3\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}1+\dfrac{5}{\sqrt{x}+2}=2\\1+\dfrac{5}{\sqrt{x}+2}=3\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}+2=5\\\sqrt{x}+2=\dfrac{5}{2}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=3\\\sqrt{x}=\dfrac{1}{2}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=9\\x=\dfrac{1}{4}\end{matrix}\right.\)
Vậy...
Bài 3.2
\(A=\dfrac{-x-2\sqrt{x}-5}{\sqrt{x}+2}\)\(=\dfrac{-\sqrt{x}\left(\sqrt{x}+2\right)-5}{\sqrt{x}+2}=-\sqrt{x}-\dfrac{5}{\sqrt{x}+2}\)
\(=2-\left(\sqrt{x}+2+\dfrac{5}{\sqrt{x}+2}\right)\)
Áp dụng bđt cosi: \(\sqrt{x}+2+\dfrac{5}{\sqrt{x}+2}\ge2\sqrt{\left(\sqrt{x}+2\right).\dfrac{5}{\sqrt{x}+2}}=2\sqrt{5}\)
\(\Rightarrow A\le2-2\sqrt{5}\)
Dấu = xảy ra \(\Leftrightarrow\sqrt{x}+2=\dfrac{5}{\sqrt{x}+2}\Leftrightarrow x=9-4\sqrt{5}\)
T
2
23 tháng 6 2021
A = \(\dfrac{2\left(3\sqrt{x}+2\right)+4}{3\sqrt{x}+2}\)
= \(2+\dfrac{4}{3\sqrt{x}+2}\)
Để A nguyên
<=> \(\dfrac{4}{3\sqrt{x}+2}\) nguyên
<=> \(4⋮3\sqrt{x}+2\)
Ta có bảngg
| \(3\sqrt{x}+2\) | 1 | -1 | 2 | -2 | 4 | -4 |
| x | \(\varnothing\) | \(\varnothing\) | 0 | \(\varnothing\) | \(\dfrac{4}{9}\) | \(\varnothing\) |
| Thử lại | tm | loại |
KL: x = 0
TK
23 tháng 6 2021
A=\(\dfrac{6\sqrt{x}+8}{3\sqrt{x}+2}\)=\(\dfrac{2(3\sqrt{x}+4)}{3\sqrt{x}+2}\)=\(2\cdot\left(1+\dfrac{2}{3\sqrt{x}+2}\right)\)
Để A∈Z
Thì \(3\sqrt{x}+2\)∈Ư(2)
Tức là \(3\sqrt{x}+2\)∈\(\left\{1;-1;2;-2\right\}\)
\(3\sqrt{x}+2=1\)(vô lí);\(3\sqrt{x}+2=-1\)(vô lí);\(3\sqrt{x}+2=-2\)(vô lí)
\(3\sqrt{x}+2=2\)=>x=0
Vì 0∈Z
Vậy x=0 thì thỏa mãn đề bài
T
2
23 tháng 6 2021
`A=(6sqrtx+8)/(3sqrtx+2)`
`=(6sqrtx+4+4)/(3sqrtx+2)`
`=2+4/(3sqrtx+2)>2AAx>=0(1)`
Vì `3sqrtx>=0`
`=>3sqrtx+2>=2`
`=>4/(3sqrtx+2)<=2`
`=>A<=4(2)`
`(1)(2)=>2<A<=4`
Mà `A in ZZ`
`=>A in {3,4}`
`**A=3`
`<=>4/(3sqrtx+2)=1`
`<=>4=3sqrtx+2`
`<=>3sqrtx=2`
`<=>x=4/9`
`**A=4`
`<=>4/(3sqrtx+2)=2`
`<=>6sqrtx+4=4`
`<=>6sqrtx=0`
`<=>sqrtx=0`
`<=>x=0`
23 tháng 6 2021
đk: \(x\ge0\)
A = \(\dfrac{2\left(3\sqrt{x}+2\right)+4}{3\sqrt{x}+2}\)
= \(2+\dfrac{4}{3\sqrt{x}+2}\)
Để A \(\in Z\)
<=> \(4⋮3\sqrt{x}+2\)
Ta có bảng:
| \(3\sqrt{x}+2\) | 1 | -1 | 2 | -2 | 4 | -4 |
| x | \(\varnothing\) | \(\varnothing\) | 0 | \(\varnothing\) | \(\dfrac{4}{9}\) | \(\varnothing\) |
| tm | tm |
T
0