K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NQ
0
9 tháng 3 2021
a, Đường phân giác góc phần tư thứ nhất là một nửa đường thẳng x - y = 0 nằm ở góc phần tư thứ nhất
=> d nhận (1 ; -1) làm vecto pháp tuyến
=> PT đi qua M (-2 ; -5) là
x + 2 - y - 5 = 0 ⇔ x - y - 3 = 0
b, c, Lười lắm ko làm đâu :)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 4 2020
14.
\(\overrightarrow{AB}=\left(-3;10\right)\) nên pt tham số của AB là: \(\left\{{}\begin{matrix}x=3-3t\\y=-4+10t\end{matrix}\right.\)
15.
Do d song song delta nên d nhận \(\left(2;-1\right)\) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=2t\\y=-4-t\end{matrix}\right.\)
18.
d có vtcp là (2;3) nên d nhận (3;-2) là 1 vtpt
Phương trình d:
\(3\left(x+1\right)-2\left(y-0\right)=0\Leftrightarrow3x-2y+3=0\)
19.
\(\overrightarrow{AB}=\left(3;-4\right)\Rightarrow\) đường thẳng AB nhận (4;3) là 1 vtpt
Phương trình d:
\(4\left(x+2\right)+3\left(y-4\right)=0\Leftrightarrow4x+3y-4=0\)
LT
7 tháng 5 2019
a)\(\overrightarrow{AC}=\left(4;0\right)\Rightarrow\overrightarrow{N}_{AC}=\left(0;4\right)\)
Phương trình đường thẳng AC : \(4y-4=0\)
Phương trình đường thẳng BH vuông góc AC : \(4x+c=0\)
Thay tọa độ điểm B được : \(c=-4\)
Phương trình đường thẳng BH :\(4x-4=0\)
LT
7 tháng 5 2019
b) \(\overrightarrow{AB}=\left(0;3\right)\)
Gọi M,N lần lượt là trung điểm AB,AC
\(M\left(1;\frac{5}{2}\right)\)
\(N\left(3;1\right)\)
Phương trình đường thẳng đi qua M vuông góc AB hay là đường trung trực AB: \(3y-\frac{15}{2}=0\)
\(\overrightarrow{AC}=\left(4;0\right)\)
Phương trình đường trung trực AC : \(4x-12=0\)
Tâm I đường tròn ngoại tiếp tam giác là nghiệm của hệ:
\(\left\{{}\begin{matrix}3y-\frac{15}{2}=0\\4x-12=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=\frac{5}{2}\end{matrix}\right.\)
\(\overrightarrow{IA}=\left(-2;-\frac{3}{2}\right)\)
\(IA=R\)
\(IA=\sqrt{\left(-2\right)^2+\left(\frac{-3}{2}\right)^2=\frac{5}{2}}\)
Phương trình đường tròn ngoại tiếp tam giác ABC: \(\left(x-3\right)^2+\left(y-\frac{5}{2}\right)^2=\frac{25}{4}\)
CM
5 tháng 6 2018
a) Phương trình đường thẳng Δ đi qua M(–5; –8) và có hệ số góc k = –3 là:
y = –3.(x + 5) – 8 ⇔ 3x + y + 23 = 0.
b) Ta có: A(2; 1), B(–4; 5) ⇒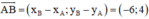 
Δ đi qua hai điểm A(2; 1) và B(–4; 5)
⇒ Δ nhận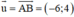 
là một vtcp
⇒ Δ nhận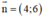 
là một vtpt.
Phương trình tổng quát của đường thẳng Δ là:
(Δ) : 4(x – 2) + 6(y -1) = 0
Hay 4x + 6y – 14 = 0 ⇔ 2x + 3y – 7 = 0.
12 tháng 4 2016
Phương trình của ∆ là : y + 8 = -3(x + 5) <=> 3x + y + 23 = 0
Gọi phương trình đường thẳng có dạng \(y=-2x+b\)
Do d qua M nên:
\(5=-2.1+b\Rightarrow b=7\)
Phương trình đường thẳng: \(y=-2x+7\Leftrightarrow2x+y-7=0\)