K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
20 tháng 3 2022
Câu 1.
Điểm M nằm cách đều hai dây:
\(\Rightarrow r_1=r_2=\dfrac{r}{2}=\dfrac{32}{2}=16cm=0,16m\)
\(B_1=4\pi\cdot10^{-7}\cdot\dfrac{I_1}{r_1}=4\pi\cdot10^{-7}\cdot\dfrac{5}{0,16}=3,93\cdot10^{-5}T\)
\(B_2=4\pi\cdot10^{-7}\cdot\dfrac{I_2}{r_2}=4\pi\cdot10^{-7}\cdot\dfrac{1}{0,16}=7,85\cdot10^{-6}T\)
Hai dây ngược chiều nahu xảy ra cảm ứng từ tại M có độ lớn:
\(B=\left|B_1-B_2\right|=\left|3,93\cdot10^{-5}-7,85\cdot10^{-6}\right|=3,145\cdot10^{-5}T\)
Câu 2.
Độ biến thiên từ thông:
\(\phi=NBS\cdot cos\alpha=20\cdot0,03\cdot10\cdot10^{-4}\cdot cos180^o=-6\cdot10^{-4}Wb\)
13 tháng 3 2022
Câu 2.
Cảm ứng từ tác dụng lên dòng \(I_1\) là:
\(B_1=2\pi\cdot10^{-7}\cdot\dfrac{I_1}{r_1}=2\pi\cdot10^{-7}\cdot\dfrac{2}{0,04}=3,14\cdot10^{-5}T\)
Cảm ứng từ tác dụng lên dòng \(I_2\) là:
\(B_2=2\pi\cdot10^{-7}\cdot\dfrac{I_2}{r_2}=2\pi\cdot10^{-7}\cdot\dfrac{4}{0,14}=1,8\cdot10^{-5}T\)
Hai dòng điện ngược chiều:
\(B=\left|B_1-B_2\right|=3,14\cdot10^{-5}-1,8\cdot10^{-5}=1,34\cdot10^{-5}T\)
13 tháng 3 2022
Câu 3.
Từ thông qua dây dẫn:
\(\phi=NBS\cdot cos\alpha=1000\cdot4\cdot10^{-2}\cdot100\cdot10^{-4}=0,4Wb\)
Độ lớn suất điện động cảm ứng:
\(\left|e_c\right|=\left|\dfrac{\Delta\phi}{\Delta t}\right|=\left|\dfrac{0,4}{1}\right|=0,4V\)
VT
10 tháng 10 2019
a. Từ
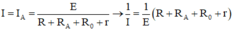
Đặt:
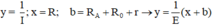
b. Căn cứ các giá trị của R và I trong phương án 1, ta tính các giá trị tương ứng của x và y.
c. Vẽ đồ thị y = f (x) biểu diễn gián tiếp mối liên hệ giữa I và R.
d. Xác định tọa độ của xm và y0 là các điểm mà đồ thị trên cắt trục hoành và trục tung.
VT
21 tháng 6 2018
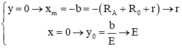
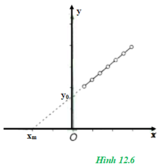
Vẽ mạch điện:
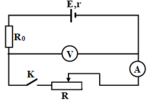
Thực hiện đo các giá trị U và I tương ứng khi thay đổi R. Vẽ đồ thị mô tả mối quan hệ đó, tức U = f(I). Áp dụng phương pháp xử lí kết quả đo được bằng đồ thị, ta vẽ được đường biểu diễn. Ở đây dự đoán là một đường thẳng có dạng y = ax + b. Đường thẳng này sẽ cắt trục tung tại U0 và cắt trục hoành tại Im. Xác định giá trị của U0 và Im trên các trục. Đồ thị vẽ được có dạng như hình sau:
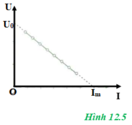
Theo phương trình đồ thị, dựa vào công thức của định luật ôm cho toàn mạch
ta có: U = E – I.(R0 + r)
Khi I = 0 ⇒ U0 = E
Khi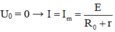 
Từ đó ta tính được E và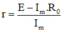 
DH
1
HT
6 tháng 1 2021
Okie, xinh nên giúp :3 Đùa thui
a/ 5 nguồn mắc nối tiếp \(\left\{{}\begin{matrix}\xi_b=5.\xi=5.4=20\left(V\right)\\r_b=5r=5.0,2=1\left(\Omega\right)\end{matrix}\right.\)
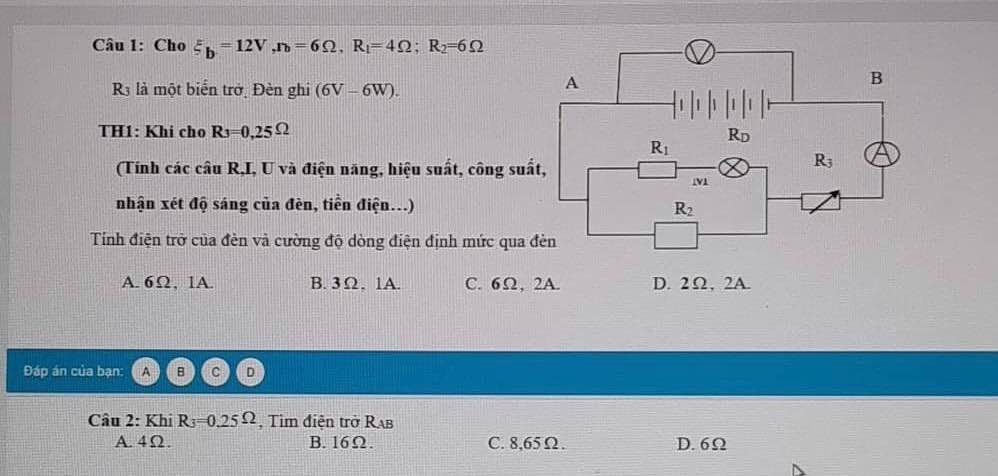
b/ \(R_D=\dfrac{U^2_{dm}}{P_{dm}}=\dfrac{36}{6}=6\left(\Omega\right);I_{dm}=\dfrac{P_{dm}}{U_{dm}}=\dfrac{6}{6}=1\left(A\right)\)
Đèn sáng bình thường \(\Rightarrow I_2=I_D=I_{dm}=1\left(A\right)\)
\(\left(R_1ntR_B\right)//\left(R_2ntR_D\right)\Rightarrow R_{td}=\dfrac{\left(R_1+R_B\right)\left(R_2+R_D\right)}{R_1+R_B+R_2+R_D}=\dfrac{\left(2+4\right)\left(6+6\right)}{2+4+6+6}=4\left(\Omega\right)\)
c/ \(I=\dfrac{\xi_b}{r_b+R_{td}}=\dfrac{20}{1+4}=4\left(A\right)\)
\(I=I_1+I_2\Rightarrow I_1=I-I_2=4-1=3\left(A\right)\Rightarrow P_1=I_1^2.R_1=3^2.2=18\left(W\right)\)
\(m_{Cu}=\dfrac{A_{Cu}.I_B.t}{F.n}=\dfrac{64.3.\left(32.60+10\right)}{96500.2}=...\left(g\right)\)
M
5 tháng 9 2023
Với phương trình x = 10cos(2πt - π/3) cm, ta cần tính quãng đường đi được từ lúc t = 0 đến lúc t = 13/6 s.
Để tính quãng đường đi được, ta sử dụng công thức sau:
Quãng đường đi được = |x(t2) - x(t1)|
Với t2 = 13/6 s và t1 = 0, ta có:
x(t2) = 10cos(2π(13/6) - π/3) cm x(t1) = 10cos(2π(0) - π/3) cm
Thay vào công thức, ta tính được quãng đường đi được.
Với phương trình x = 20cos(10πt + π/6) cm, ta cần tính thời điểm vật đi qua vị trí M có li độ 10 cm lần thứ 2023.Để tính thời điểm vật đi qua vị trí M, ta sử dụng công thức sau:
t = (1/10π)arccos((x - 10)/20) - π/6
Thay vào công thức, ta tính được thời điểm vật đi qua vị trí M lần thứ 2023.
Vậy, ta đã giải được bài toán.
DN
0
19 tháng 1 2022
Đổi : 20 cm = 0,2 m
Cảm ứng từ tại tâm O :
\(B_o=2\pi.10^{-7}\dfrac{I}{r}=2\pi.10^{-7}\dfrac{3+4}{0,2}=7.10^{-6}\left(T\right)\)
tự luận thì bạn up từng câu 1 lên nhé =)) Đăng nguyên cái đề lên k có ai làm đâu =))))))