Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ pt \(v=16\pi\cos\left(4\pi t-\dfrac{\pi}{6}\right)=16\pi\cos\left(4\pi t-\dfrac{2\pi}{3}+\dfrac{\pi}{2}\right)\) (cm/s), ta suy ra \(\omega=4\pi\left(rad/s\right)\), lại có \(\omega A=16\pi\Leftrightarrow A=\dfrac{16\pi}{\omega}=4\left(cm\right)\)
\(\varphi_0=-\dfrac{2\pi}{3}\); \(T=\dfrac{2\pi}{\omega}=0,5\left(s\right)\)
Đường tròn lượng giác:
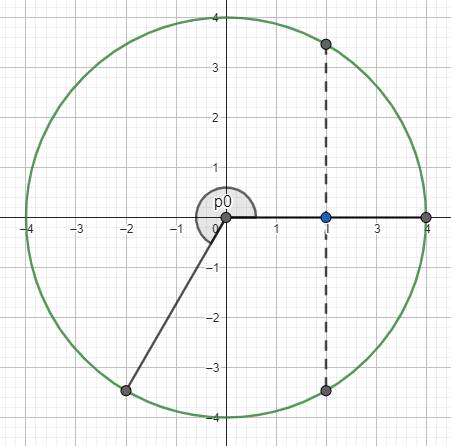
Từ đây, ta có thể thấy tại thời điểm lần thứ 2023 vật chuyển động qua vị trí \(x=2\) kể từ khi dao động, góc quét của vật là \(\Delta\varphi=\dfrac{\pi}{3}+1011.2\pi=\dfrac{6067}{3}\pi\) (rad)
Thời điểm lần thứ 2023 vật chuyển động qua vị trí \(x=2\) kể từ lúc bắt đầu dao động là \(\Delta t=\dfrac{\Delta\varphi}{2\pi}.T=\dfrac{\dfrac{6067}{3}\pi}{2\pi}.0,5=\dfrac{6067}{12}\approx505,58\left(s\right)\)

\(T=\dfrac{2\pi}{w}=\dfrac{2\pi}{\pi}=2\left(s\right)\)
Trong 1 nửa chu kì, vật di chuyển được quãng đường là \(2\cdot10=20\left(cm\right)\)
Vật khi đó phải đi từ vị trí có pha bằng \(-\dfrac{\pi}{3}\) đến vị trí có pha bằng \(\dfrac{\pi}{3}\), vì vật sẽ di chuyển được quãng đường \(\dfrac{A}{2}+\dfrac{A}{2}=A=10\left(cm\right)\)
Vậy thời gian vật phải đi là: \(\dfrac{T}{2}+\dfrac{T}{6}=\dfrac{2}{2}+\dfrac{2}{6}=\dfrac{4}{3}\left(s\right)\)

Ta có : \(A=4cm\)
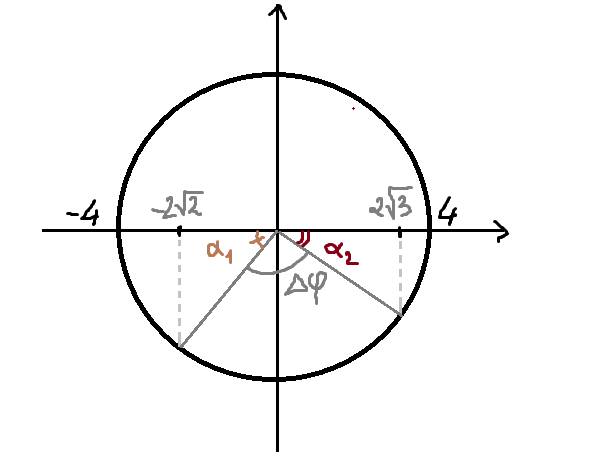
\(cos\alpha_1=\dfrac{-2\sqrt{2}}{4}=-\dfrac{\sqrt{2}}{2}\Rightarrow\alpha_1=\dfrac{3\pi}{4}rad\)
\(cos\alpha_2=\dfrac{2\sqrt{3}}{4}=\dfrac{\sqrt{3}}{2}\Rightarrow\alpha_2=\dfrac{\pi}{6}rad\)
\(\Delta\varphi=\left(\dfrac{\pi}{2}-\dfrac{3\pi}{4}\right)+\left(\dfrac{\pi}{2}-\dfrac{\pi}{6}\right)=\dfrac{\pi}{12}rad\)
Có : \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{\pi}=2s\)
\(\Delta t=\dfrac{\Delta\varphi}{2\pi}.T=\dfrac{\dfrac{\pi}{12}}{2\pi}.2=\dfrac{1}{12}s\)
Vậy ...
Hình ảnh biểu diễn :

Câu 1.
a)Tốc độ góc: \(\omega=2\pi f=2\pi\)
Ta có: \(A=\sqrt{x^2+\dfrac{v^2}{\omega^2}}=\sqrt{0,05^2+\dfrac{\left(0,10\pi\right)^2}{\left(2\pi\right)^2}}=\dfrac{\sqrt{2}}{20}m\)
b)Phương trình vận tốc:
\(v=-\omega Asin\left(\omega t+\varphi\right)=-2\pi\cdot\dfrac{\sqrt{2}}{20}sin\left(2\pi t\right)\)
Câu 2.
a)Chu kỳ: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{5\pi}=0,4s\)
b)Li độ tại thời điểm \(t=2s:\)
\(x=2cos\left(5\pi t+\dfrac{\pi}{3}\right)=2cos\left(5\pi\cdot2+\dfrac{\pi}{3}\right)=1\)

Biên độ dao động là A=40/2=20cm
Phương trình dao động là: \(x=20\cdot cos\left(w\cdot t+pi\right)\)
Theo đề, ta có: \(w=\dfrac{v}{\sqrt{A^2-x^2}}=\dfrac{20pi\cdot\sqrt{3}}{\sqrt{20^2-10^2}}=2pi\)
Phương trình dao động là: \(x=20\cdot cos\left(2pi\cdot t+pi\right)\)
Để tính quãng đường đi được, ta sử dụng công thức sau:
Quãng đường đi được = |x(t2) - x(t1)|
Với t2 = 13/6 s và t1 = 0, ta có:
x(t2) = 10cos(2π(13/6) - π/3) cm x(t1) = 10cos(2π(0) - π/3) cm
Thay vào công thức, ta tính được quãng đường đi được.
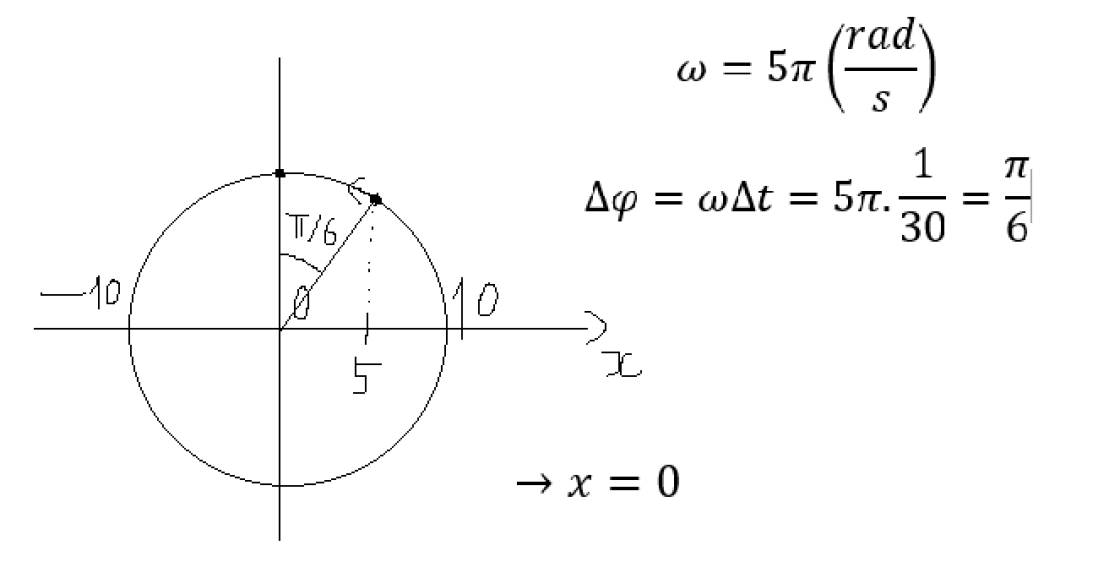
Với phương trình x = 20cos(10πt + π/6) cm, ta cần tính thời điểm vật đi qua vị trí M có li độ 10 cm lần thứ 2023.Để tính thời điểm vật đi qua vị trí M, ta sử dụng công thức sau:
t = (1/10π)arccos((x - 10)/20) - π/6
Thay vào công thức, ta tính được thời điểm vật đi qua vị trí M lần thứ 2023.
Vậy, ta đã giải được bài toán.