
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Tam giác OAC là tam giác vuông. Vì AC là đường cao của tam giác vuông OAC, và đường cao luôn vuông góc với cạnh đối diện nên tam giác OAC là tam giác vuông tại A. b) Ta có CH vuông góc với AB tại H và AC vuông góc với BC. Theo định lý Euclid, trong một tam giác vuông, bình phương của độ dài đường cao bằng tích của độ dài đoạn thẳng từ đỉnh vuông góc đến điểm chia cạnh huyền. Vì vậy, CH^2 = AH * HB. c) Vì K là trung điểm của BC, nên BK = KC. Do đó, K nằm trên đường tròn (O) với đường kính BC. d) Gọi I là trung điểm của CH. Ta biết rằng AI là đường phân giác của góc OAC. Vì OAC là tam giác vuông tại A, nên AI cũng là đường phân giác của góc OAB. Do đó, AI cắt đường tròn (O) tại một điểm E. Để tính AE.BD + OK.OD, ta cần biết thêm thông tin về vị trí của các điểm A, B, C, D, E, O, K và H trên đường tròn (O) và tam giác OAC.
______________________HT____________________________

Bài 8:
\(P=\left(2+\sqrt{a}\right)\left(2-\sqrt{a}\right)=4-a\)

Bài 2:
gọi thời gian chảy riêng từng vòi đầy bể lần lượt là x(giờ) và y(giờ)
(Điều kiện: x>0 và y>0)
Trong 1h, vòi thứ nhất chảy được \(\dfrac{1}{x}\left(bể\right)\)
Trong 1h, vòi thứ hai chảy được \(\dfrac{1}{y}\left(bể\right)\)
TRong 1h, hai vòi chảy được \(\dfrac{1}{4}\left(bể\right)\)
=>\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\left(1\right)\)
Trong 10h, vòi thứ nhất chảy được \(\dfrac{10}{x}\left(bể\right)\)
Nếu mở vòi thứ nhất chảy trong 10 giờ rồi khóa lại và mở vòi thứ hai chảy trong 1 giờ nữa thì đầy bể nên ta có:
\(\dfrac{10}{x}+\dfrac{1}{y}=1\left(2\right)\)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\\\dfrac{10}{x}+\dfrac{1}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{9}{x}=-\dfrac{3}{4}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=12\\\dfrac{1}{y}=\dfrac{1}{4}-\dfrac{1}{12}=\dfrac{3}{12}-\dfrac{1}{12}=\dfrac{2}{12}=\dfrac{1}{6}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=12\\y=6\end{matrix}\right.\left(nhận\right)\)
Vậy: Thời gian để vòi một chảy một mình đầy bể là 12 giờ
Thời gian để vòi thứ hai chảy một mình đầy bể là 6 giờ

a: \(A=\dfrac{\sqrt{a}+\sqrt{b}}{\sqrt{ab}}\cdot\left(\dfrac{a\sqrt{a}+a\sqrt{b}-b\sqrt{a}-b\sqrt{b}-a\sqrt{a}+b\sqrt{b}}{a-b}\right)\)
\(=\dfrac{1}{\sqrt{ab}}\cdot\dfrac{\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}=1\)
b: \(=\dfrac{\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}-\sqrt{a}+1\right)}{\left(a-1\right)\left(a+1\right)}\)
\(=\dfrac{\left(a-1\right)^2}{\left(a-1\right)\left(a+1\right)}=\dfrac{a-1}{a+1}\)

2b)
xét vế trái ta có
=\(\left(\sqrt{x}-\sqrt{y}\right).\dfrac{\sqrt{x^2y}+\sqrt{xy^2}}{\sqrt{xy}}\) \(\left(\sqrt{x}-\sqrt{y}\right).\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{xy}}\)=x-y
3b)
để A<0 \(\Rightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}}< 0\)
\(\Rightarrow\sqrt{x}-1< 0\)\(\Rightarrow\sqrt{x}< 1\)\(\Rightarrow x< 1\)
a: Ta có: \(\sqrt{9x^2-6x+1}=5\)
\(\Leftrightarrow\left|3x-1\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=5\\3x-1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=6\\3x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{4}{3}\end{matrix}\right.\)


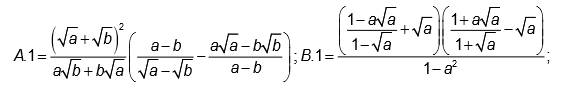 cao nhân nào giúp tui làm 2 câu này với :<<
cao nhân nào giúp tui làm 2 câu này với :<<
b) Ta có: \(\angle MEI+\angle MBI=90+90=180\Rightarrow\) MEIB nội tiếp
\(\Rightarrow\angle IME=\angle IBE=\angle ABD=45\)