

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Quãng đường Trái Đất đi được sau 3 giây là :
29,8 x 3 = 89,4 ﴾ km ﴿
Vận tốc của Sao Hỏa khi chuyển động xung quanh Mặt Trời là :
29,8 + 5,7 = 35,5 ﴾ km/giờ ﴿
Quãng đường Sao Hỏa đi được sau 3 giây là :
35,5 x 3 = 106 ,5 ﴾ km ﴿
Đ/S : Trái Đất : 89,4 km ; Sao Hỏa : 106,5 km

Đáp án B
Đặt E B = a như hình vẽ ⇒ E F = a A E = 6 − a .
Trong tam giác vuông AEF có
cos A E F ^ = 6 − a a ⇒ cos F E B ^ = a − 6 a (hai góc bù nhau).
Ta có
Δ B E G = Δ F E G ⇒ F E G ^ = B E G ^ = 1 2 F E B ^ ⇒ cos F E G ^ = a − 3 a
Trong tam giác vuông AEF có E G = E F cos F E G ^ = a 3 a − 3 .
Xét hàm f a = a 3 a − 3 với a > 3 , ta được min f a đạt tại a = 9 2 ⇒ E G = 9 3 2 .

Theo đề ta có:
Đoạn FE là
FE= 200. 2= 400 (km)
Vận tốc xe thứ 3 là:
50. 2= 100 ( km)
Quang đường xe thứ 3 nhiều hơn xe thứ 2 là;
200 + 10= 210 ( km)
Hiệu của hai vận tốc là:
100- 4= 60 ( km)
Thời gian 2 xe gặp nhau và gấp đôi xe thứ hất là:
210 : 60=3,5 ( giờ)
Khoảng cách đến C của xe thứ nhất gấp đôi xe thứ 2 cần số giờ là:
7 + 3,5= 10,5 ( giờ)
Đổi 10,5 giờ= 10 giờ 30 phút
Vậy: Khoảng cách đến C của xe thứ nhất gấp đôi xe thứ 2 cần 10 giờ 30 phút

Đáp án C.
Màn biểu diễn của Dynano được biểu diễn theo mô hình bên
Cách 1: Áp dụng kiến thức “Giá trị lớn nhất – Giá trị nhỏ nhất của hàm số”
Ta có A B = c , A C = a , A D = b , A M = x . Khi đó C M = A C 2 + A M 2 = x 2 + a 2
Và
M D = B M 2 + B D 2 = ( c − x ) 2 + b 2 = x 2 − 2 c x + b 2 + c 2
Như vậy quãng đường di chuyển của Dynano là
T = C M + M D = x 2 + a 2 + x 2 − 2 c x + b 2 + c 2 ( 0 < x < c ) .
Xét hàm số x 2 + a 2 + x 2 − 2 c x + b 2 + c 2 trên ( 0 ; c ) .
Đạo hàm f ' ( x ) = x x 2 + a 2 + x − c x 2 − 2 c x + b 2 + c 2 = 0
⇔ x x 2 − 2 c x + b 2 + c 2 = ( c − x ) x 2 + a 2 ⇔ x 2 c − x 2 + b 2 = c − x 2 x 2 + a 2
⇔ x 2 b 2 = c - x 2 a 2 ⇔ b x = ( c − x ) a ⇔ x = a c a + b ∈ ( 0 ; c ) .
Lập bảng biến thiên tìm ta được f(x) đạt nhỏ nhất khi x = a c a + b .
Cách 2: Dùng kiến thức hình học
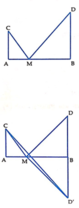
Gọi D' là điểm đối xứng với D qua AB. Khi đó M C + M D = M C + M D ' ≥ C D ' . Do vậy ( M C + M D ) min = C D ' . Dấu = xảy ra khi M ∈ C D ' hay M = C D ' ∩ A B .
Khi đó Δ A M C ∽ △ B M D '
⇒ A M B M = A C B D ' ⇔ x c − x = a b ⇔ x = a c a + b