Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ở nhiệt độ t0 (ºC) cạnh hình lập phương là l0
→ thể tích khối lập phương là:
Ở nhiệt độ t (ºC) cạnh hình lập phương là l
→ thể tích khối lập phương là: V = l3
Mặt khác ta có: l = l0.(1 + αΔt) ⇒ V = l03.(1 + αΔt)3
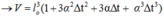
Do α rất nhỏ nên α2 và α3 cũng rất nhỏ, ta có thể bỏ qua.
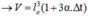
→ ΔV = V – V0 = V0.β.Δt

+ Gọi V0 là thể tích của khối lập phương ở 0oC:
V0 = l03
+ V là thể tích của khối lập phương ở t0C:
V = l3 = [l0(1+ α∆t)]3 = l03 (1+α∆t)3
Mà (1+ α∆t)3 = 1 + 3α∆t + 3α2∆t2 + α3∆t3
Vì α khá nhỏ nên α2, α3 có thể bỏ qua.
=> V = l3 = l03 (1+ 3α∆t) = Vo (1+ β∆t) với β = 3α.

B3: mốc thế năng tại vị trí ném
a, W= 1/2.0,1.82 + 0,1.10.4 = 7,2
b, BTCN: 0,1.10.z1 = 7,2
=> z1 = 7,2m
e, BTCN: Wd + Wt = 7,2
=> 3/2.1/2.0,1.V22 = 7,2
=> V2 = \(\sqrt{96}\approx9,8\) m/s
f, BTCN: 1/2.0,1.V12 + 0,1.10.6 = 7,2
=> V1 \(=\sqrt{24}\approx4,9\) m/s
c, BTCN: 1/2.0,1.V2 + 0,1.10.(-4)= 7,2
=> \(V=\sqrt{224}\approx15\) m/s
d, BTCN: 2.0,1.10.z' = 7,2
=> z' = 3,6m
g, BTCN: 1/2.0,1.32 + 0,1.10.z2 = 7,2
=> z2 = 6,75m

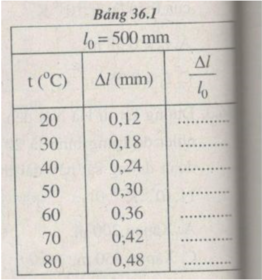
Hình 36.1G có dạng đoạn thẳng.
Điều này chứng tỏ độ biến dạng tỉ đối ∆ l/ l 0 của thanh sắt tỉ lệ thuận với độ tăng nhiệt độ t (tính từ 0 ° C):
∆ l/ l 0 = α t
Nhận xét thấy hệ số tỉ lệ α chính là hệ số nở dài của thép.
Hệ số tỉ lệ α được xác định bởi hệ số góc của đường biểu diễn đồ thị ở Hình 36.1G.
Trong trường hợp vật rắn là một tấm kim loại mỏng phẳng biến dạng nhiệt của vật rắn coi như biến dạng về diện tích. Ta có thể áp dụng công thức độ nở diện tích: ∆ S = S - S 0 = β ' S 0 ∆ t = 2 α S 0 ∆ t
+ ΔS: độ nở diện tích của vật rắn
+ S: diện tích sau khi giãn nở vì nhiệt của vật rắn
+ S0: diện tích ban đầu của vật rắn
+ β′ = 2α: hệ số nở diện tích, phụ thuộc vào bản chất của vật rắn
+ Δt = t2 − t1: độ tăng nhiệt độ của vật rắn
Đáp án: D