Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tế bào đang ở kì giữa của quá trình giảm phân II
Giải thích : Trên tiêu bản, ta thấy có 5 NST kép (số lẻ) xếp thành hàng nên suy ra được các NST không đi thành từng cặp tương đồng
=> Chỉ có thể là quá trình giảm phân, mak các NST xếp thành 1 hàng nên lak Kì giữa II
b) Trước tiên ta tìm được bộ NST 2n của loài lak 2n = 10
(* Do ở kì giữa II có n NST kép = 5 nên 2n sẽ = 10)
-> Số NST đơn môi trường cung cấp cho quá trình nguyên phân :
\(2n.\left(2^5-1\right)=10.\left(2^5-1\right)=310\left(NST\right)\)
* Ở đây đề thiếu nên mik nghĩ tiếp theo đề hỏi lak Tạo ra bao nhiêu loại giao tử và đó lak loại nào ?
- Ta xét cặp NST XY : Do không phân li trong giảm phân 1 nên sẽ tạo ra 2 loại giao tử với tỉ lệ ngang nhau lak XY và 0
-> Số loại giao tử tạo ra : \(2^3=8\left(loại\right)\)
Các loại giao tử đó là : \(ABDeXY\) và \(ABDe0\) và \(AbDeXY\) và \(AbDe0\) và \(aBDeXY\) và \(aBDe0\) và \(abDeXY\) và \(abDe0\)

a) Gọi 2n lak bộ NST lưỡng bội của loài, x lak số lần nguyên phân (x, 2n ∈ N*)
Ta có :
* Tb nguyên phân x lần cho số tb con bằng 1/3 số NST trong bộ đơn bội
-> \(2^x=\dfrac{1}{3}.n\) (1)
Lại có : + Môi trường nội bào cung cấp 168 NST đơn
-> \(2n.\left(2^x-1\right)=168\) (2)
Từ (1) và (2) ta có hệ phương trình : \(\left\{{}\begin{matrix}2^x=\dfrac{1}{3}n\\2n.\left(2^x-1\right)=168\end{matrix}\right.\)
Giải hệ phương trình ta được : n = 12
-> 2n = 24
Vậy bộ NST lưỡng bội của loài trên lak 2n = 24
b) Có 2n = 24, thay vào (2) ta được : \(24.\left(2^x-1\right)=168\)
=> \(2^x=\dfrac{168}{24}+1=8\)
=> \(x=3\)
Vậy số lần nguyên phân của tb trên lak 3 lần

GP là quá trình tb phân chia từ bộ nst (2n) giảm đi 1 nửa còn ( n) . Do quá trình GP chỉ 1 lần nhân đôi và 2 lần phân chia nên tb tạo ra là 4 với mỗi tb có n nst => đáp án A
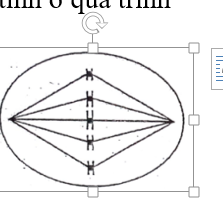
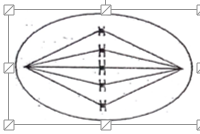
Kì giữa nguyên phân
Bộ NST 2n=8
Kỳ giữa giảm phân II ; Bộ NST 2n = 2.5 = 10
(vik ta thấy tiêu bản chỉ có 5 NST xếp thành 1 hàng -> số lẻ nên chỉ có thể lak giảm phân II )