Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn
Nên đường tròn có vô số trục đối xứng

CO cắt AB tại D
Vì \(OA=OB=R\Rightarrow\Delta OAB\) cân tại O có \(OD\bot AB\Rightarrow D\) là trung điểm AB
\(\Rightarrow\) A và B đối xứng qua OC \(\Rightarrow\left\{{}\begin{matrix}\angle OAB=\angle OBA\\\angle CAB=\angle CBA\end{matrix}\right.\)
\(\Rightarrow\angle OAB+\angle CAB=\angle OBA+\angle CBA\Rightarrow\angle CAO=\angle CBO\)
\(\Rightarrow\angle CBO=90\Rightarrow CB\) là tiếp tuyến

- Tâm của đường tròn là tâm đối xứng của đường tròn đó.
- Mọi dường kính của đường tròn đều là trục đối xứng của đường tròn.

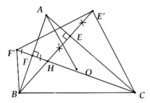
a, ∆CHE' cân tại C => C E ' H ^ = C H E ' ^
DBHF' cân tại B => B F ' H ^ = B H F ' ^
Mà => C H E ' ^ = B H F ' ^ (đối đỉnh)
=> C E ' H ^ = B F ' H ^
=> Tứ giác BCE'F' nội tiếp đường tròn tâm (O)
b, Có B F C ' ^ = B E ' C ^ = C H E ' ^ = C A B ^
Vậy A, F', E' cùng chắn BC dưới góc bằng nhau
=> 5 điểm B, F', A, E', C cùng thuộc một đường tròn tâm (O)
c, AF' = AE' (=AH) => AO là trung trực của EF => AO ^ E'F'. DHE'F' có EF là đường trung bình => EF//E'F'
=> AO ^ FE
d, A F H ^ = A E H ^ = 90 0 => AFHE nội tiếp đường tròn đường kính AH. Trong (O): Kẻ đường kính AD, lấy I trung điểm BC
=> OI = 1 2 AH, BC cố định => OI không đổi
=> Độ dài AH không đổi
=> Bán kính đường tròn ngoại tiếp ∆AEF không đổi
Đáp án D
Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn
Nên đường tròn có vô số trục đối xứng