Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì đó là số chia hết cho 5 nên số tận cùng phải là 5 hoặc 0
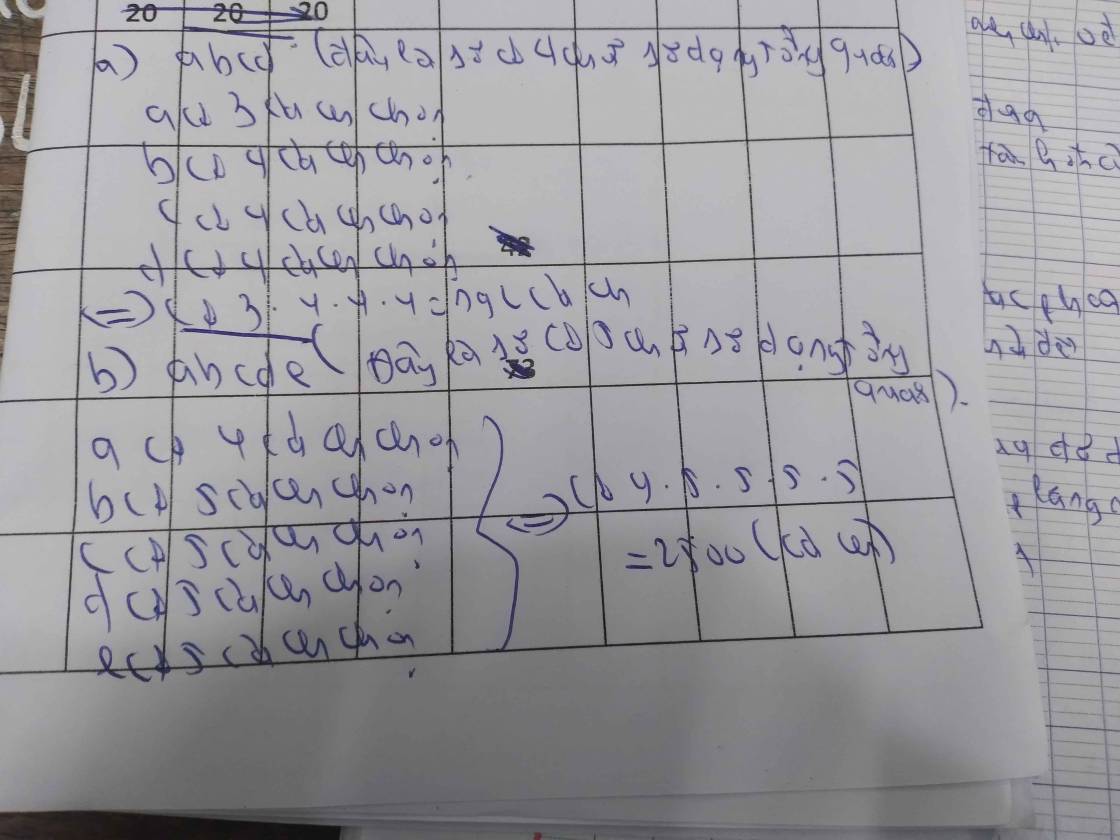
ta có số cần tìm là : abcd
TH1 : d = 0
ta có a có 4 cách chọn
b có 3 cách chọn
c có 2 cách chọn
=> 4x3x2 = 24 cách chọn
TH2 : d = 5
ta có a có 3 cách chọn ( vì a không thể = 0 )
b có 3 cách chọn
c có 2 cách chọn
=> 3x3x2 = 18 cách chọn
ĐS : 24 + 18 = 42 cách chọn

XÉT: hàng nghìn được 4 trường hợp.
hàng trăm được 3 trường hợp
hàng chục được 2 trường hợp
hàng đơn vị có 1 trường hợp
(các trường hpowj trong mỗi hàng không thể giống nhau vì 4 chữ số phải khcs nhau)
VẬY VIẾT ĐƯỢC TẤT CẢ 10 SỐ TỰ NHIÊN CÓ 4 C/S MÀ CÁC C/S ĐỀU KHÁC NHAU.
K MK NHA. CHÚC BN HỌC TỐT. ^_^

Bài 1 :
a) => Ta có dãy : 1,2,3,...,19
Vậy có số số tự nhiên nhỏ hơn 20 là:
(19-1):1+1 = 19 số
b) với n là vô hạn
c) với n là vô hạn
Bài 2 :
Ta có abc là chính
=> có thể lập các cách sau :
+ abc , acb
+ bac , bca
+ cab , cba
Vậy có thể lập được 6 số có 3 chữ số như vậy
bài 3 : gọi 5 chữ số đó là abcde
Tương tự bài 2 có thể lập lần lượt các chữ số thay thế đứng đầu :
- Ta có các dạng 3 chữ số như sau : abc , abd , acd , ace , ade , abe ( Tương tự có tất cả 5 chữ số => có 6.5 = 30 dạng tương tự )
- Mà mỗi dạng có thể lập được 3 chữ số
Vậy => 6.30 = 180 số
Bài 4 :
=> + Từ 3 đến 9 cần 7 chữ số
+ Từ 10 đến 99 cần 180 chữ số
+ Từ 100 đến 132 cần 99 chữ số
Vậy cần số chữ số để đánh hết quyển sách đó là :
7+180+99 = 286 chữ số

Chỉ có 3 chữ số 1; 2; 3 có thể ở vị trí hàng nghìn. Các vị trí hàng trăm, hàng chục và hàng đơn vị của các chữ số 0; 1; 2; 3 là như nhau. Các số thỏa mãn đề bài là:
1023; 1032; 1203; 1230; 1302; 1320; 2013; 2031; 2103; 2130; 2301; 2310; 3012; 3021; 3102; 3120; 3201; 3210.
Vậy tập hợp các số có bốn chữ số khác nhau được viết bởi các chữ số 0; 1; 2; 3 gồm 18 phần tử


A có 4 lựa chọn
B có 3 lựa chọn
Vậy viết được tất cả : 4 x 3 = 12 (số)