
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



4:
a: Xét ΔCAB vuông tại C có CH là đường cao
nên CH^2=HA*HB
=>CH=căn 2*8=4cm
Xét ΔACB vuông tại C có CH là đường cao
nên CA^2=CH*CB và CB^2=BH*BA
=>CA^2=2*10=20 và CB^2=8*10=80
=>CA=2căn 5(cm) và CB=4căn 5(cm)
b: Xét tứ giác CMHN có
góc CMH+góc CNH=180 độ
=>CMHN là tứ giác nội tiếp
=>C,M,H,N cùng thuộc 1 đường tròn

a: \(P=\dfrac{a+1+\sqrt{a}}{a+1}:\dfrac{a+1-2\sqrt{a}}{\left(\sqrt{a}-1\right)\left(a+1\right)}\)
\(=\dfrac{a+\sqrt{a}+1}{a+1}\cdot\dfrac{\left(a+1\right)\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-1\right)^2}=\dfrac{a+\sqrt{a}+1}{\sqrt{a}-1}\)
b: P<1
=>P-1<0
=>\(\dfrac{a+\sqrt{a}+1-\sqrt{a}+1}{\sqrt{a}-1}< 0\)
=>căn a-1<0
=>0<a<1
c: Thay x=19-8căn3 vào P, ta được:
\(P=\dfrac{19-8\sqrt{3}+4+\sqrt{3}+1}{4+\sqrt{3}-1}=\dfrac{31-15\sqrt{3}}{2}\)

a) Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HC^2\)
\(\Leftrightarrow AH^2=15^2-9^2=144\)
hay AH=12(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC=\dfrac{12^2}{9}=16\left(cm\right)\)

Bài 1:
a) \(\sqrt{2x+6}\) có nghĩa khi:
\(2x+6\ge0\)
\(\Leftrightarrow2x\ge-6\)
\(\Leftrightarrow x\ge-3\)
b) \(\sqrt{\dfrac{-2}{2x-3}}\) có nghĩa khi:
\(\left\{{}\begin{matrix}\dfrac{-2}{2x-3}\ge0\\2x-3\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-3\le0\left(\text{vì: }-2< 0\right)\\2x\ne3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{3}{2}\\x\ne\dfrac{3}{2}\end{matrix}\right.\)
\(\Leftrightarrow x< \dfrac{3}{2}\)
Bài 2:
a) \(\sqrt{\left(1+2\sqrt{3}\right)^2}-5\sqrt{3}\)
\(=1+2\sqrt{3}-5\sqrt{3}\)
\(=1-3\sqrt{3}\)
b) \(3\sqrt{2}+4\sqrt{8}-\sqrt{18}\)
\(=3\sqrt{2}+4\cdot2\sqrt{2}-3\sqrt{2}\)
\(=8\sqrt{2}\)
c) \(\dfrac{1}{3+\sqrt{2}}+\dfrac{1}{3-\sqrt{2}}\)
\(=\dfrac{3-\sqrt{2}}{\left(3+\sqrt{2}\right)\left(3-\sqrt{2}\right)}+\dfrac{3+\sqrt{2}}{\left(3+\sqrt{2}\right)\left(3-\sqrt{2}\right)}\)
\(=\dfrac{3-\sqrt{2}+3+\sqrt{2}}{9-2}\)
\(=\dfrac{6}{7}\)


ĐKXĐ: \(m\ne-1,m\ne\dfrac{3}{2}\)
a) 2 đường thẳng song song
\(\Leftrightarrow\left\{{}\begin{matrix}m+1=3-2m\\n\ne-2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{2}{3}\left(tm\right)\\n\ne-2\end{matrix}\right.\)
b) 2 đường thẳng cắt nhau tại một điểm trên trục tung:
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1;m\ne\dfrac{3}{2}\\m+1\ne3-2m\\n=-2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1;m\ne\dfrac{3}{2};m\ne\dfrac{2}{3}\\n=-2\end{matrix}\right.\)

b, PTGD (d1) và trục hoành là \(2x+5=0\Leftrightarrow x=-\dfrac{5}{2}\Leftrightarrow B\left(-\dfrac{5}{2};0\right)\Leftrightarrow OB=\dfrac{5}{2}\)
PTGD (d2) và trục hoành là \(2-x=0\Leftrightarrow x=2\Leftrightarrow A\left(2;0\right)\Leftrightarrow OA=2\)
Do đó \(AB=OA+OB=\dfrac{9}{2}\)
PTHDGD (d1) và (d2) là \(2x+5=2-x\Leftrightarrow x=-1\Leftrightarrow y=3\Leftrightarrow C\left(-1;3\right)\)
Gọi H là chân đg cao từ C tới Ox thì \(CH=3\)
Do đó \(S_{ABC}=\dfrac{1}{2}CH\cdot AB=\dfrac{1}{2}\cdot\dfrac{9}{2}\cdot3=\dfrac{27}{4}\left(đvdt\right)\)
c, Vì \(-1=-1;2\ne4\) nên (d2)//(d3)

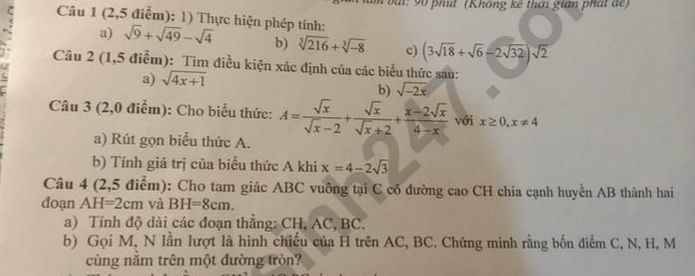



 mọi người giúp mik bài 4 câu a vs ạ
mọi người giúp mik bài 4 câu a vs ạ 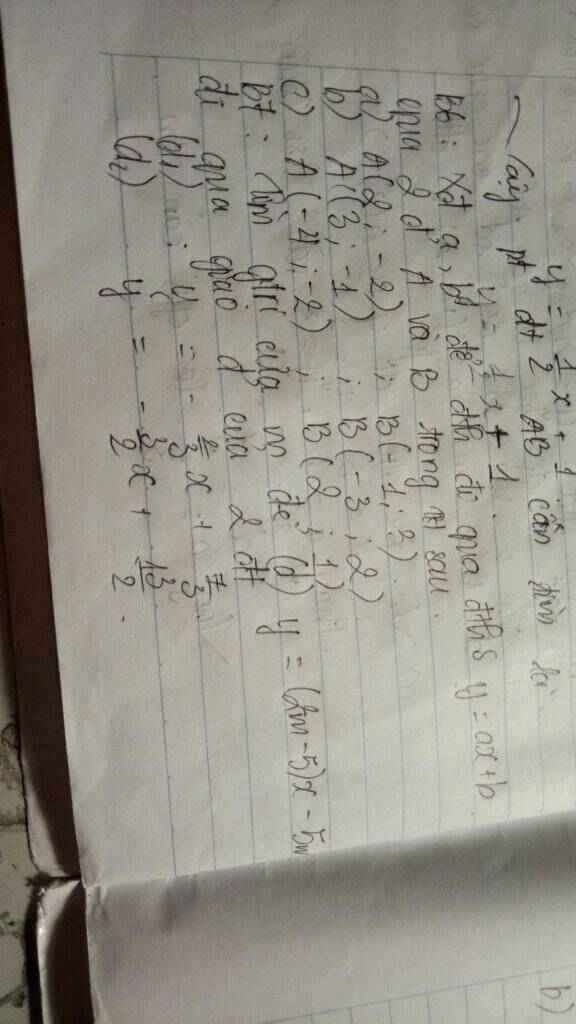
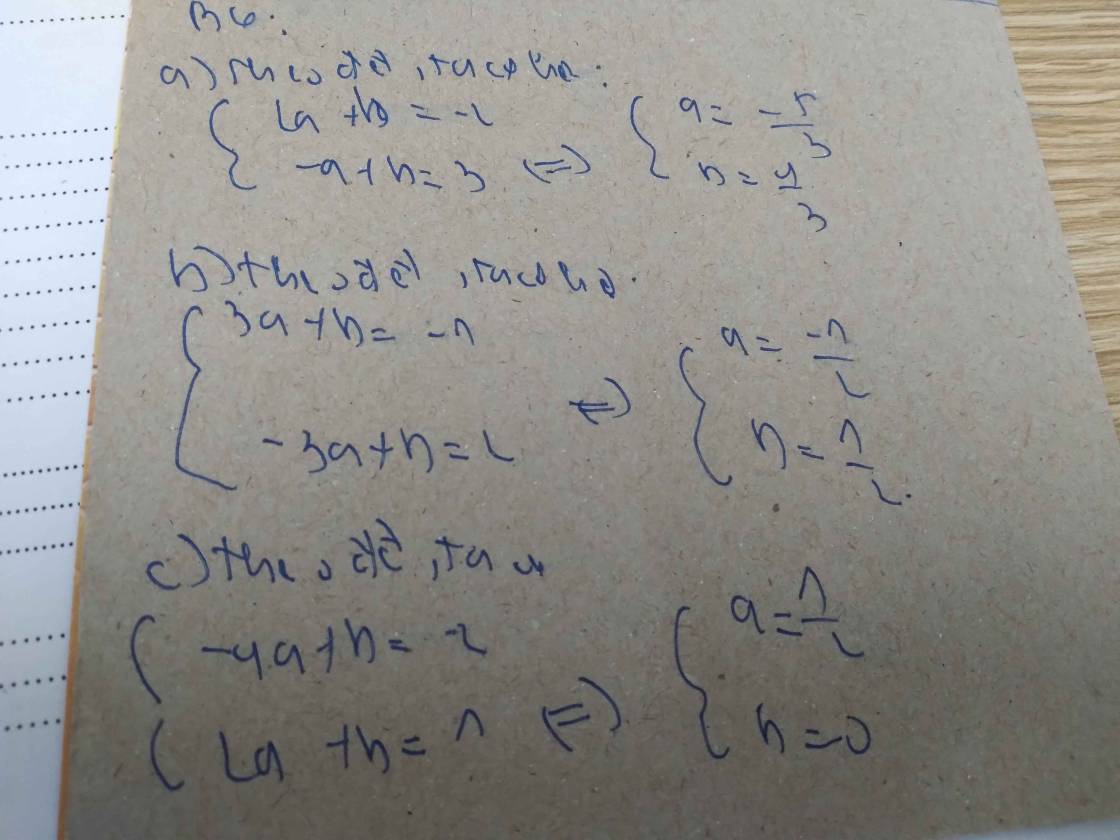


Bài đâu bạn?