Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
h = 3 cos π t 6 + π 3 + 12
Vì − 1 ≤ cos π t 6 + π 3 ≤ 1 ⇒ 9 ≤ h ≤ 15
max h = 15 ⇔ cos π t 6 + π 3 = 1 ⇔ π t 6 + π 3 = k 2 π ⇔ t = − 2 + 12 k
Thời gian ngắn nhất ⇒ t = − 2 + 12 = 10 ( h )
Đáp án D
Cách giải:
Đặt π t 14 = u ⇒ u ∈ 0 ; 12 π 7 khi đó ta có h = 2 sin 3 u 1 − 4 sin 2 u + 12
Đặt ⇔ h = 2 3 sin u − 4 sin 3 u 1 − 4 sin 2 u + 12
6 t − 24 t 3 − 8 t 3 + 32 t 5 + 12
32 t 5 − 32 t 3 + 6 t − 12
Xét u ∈ 0 ; π 2 ⇒ v ∈ 0 ; 1
Dùng [MODE] [7] ta có 
: trong khoảng có 1 lần hàm số đạt giá trị bằng 13.
trong khoảng có 1 lần hàm số đạt giá trị bằng 13.
trong khoảng có 1 lần hàm số đạt giá trị bằng 13.
Vậy v ∈ 0 ; 1 thì có 3 lần f v = 13.
Xét u ∈ π 2 ; π ⇒ v ∈ 0 ; 1 . Tương tự như trên ta có 3 lần f v = 13.
Xét u ∈ π ; 3 π 2 ⇒ v ∈ − 1 ; 0 có 2 lần f v = 13.
Xét u ∈ 3 π 2 ; 12 π 7 ⇒ v ∈ − 1 ; sin 12 π 7 ⇒ có 1 lần f v = 13.
Vậy có tất cả 9 lần mực nước trong kênh đạt độ sâu 13m.
Đáp án B.
Ta có h ( t ) = ∫ h ' ( t ) d t = 3 2000 ( t + 3 ) 4 3 + C
Lúc ban đầu t = 0 hồ bơi không có nước tức là:
h ( t ) = 0 ⇔ 3 2000 0 + 3 4 3 + C = 0 ⇔ C = - 3 7 3 2000
⇒ Mực nước bơm tại thời điểm t là: h ( t ) = 3 2000 ( t + 3 ) 4 3 - 3 7 3 2000
Theo giả thiết ⇒ h ( t ) = 3 4 . 280 ⇔ 3 2000 t + 3 4 3 - 3 7 3 2000 = 210
⇔ t + 3 4 3 = 140004 , 33 ⇔ t = 7232 ( s ) ⇒ t = 2 giờ 34 giây.
Đáp án D
Vận tốc của con cá khi bơi ngược dòng được là v - 3 (km/h)
Thời gian cá bơi được quãng đường 240km là 
Năng lượng tiêu hao của cá để vượt quãng đường đó là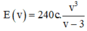 
Bài toán trở thành tìm v>3 để E(v) là nhỏ nhất.
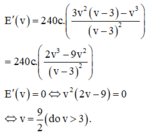
Vậy v=92 thỏa mãn đề bài.
Đáp án A
Ta có: v − 6 t = 300 ⇒ t = 300 v − 6
Vậy E = c v 3 300 v − 6 Bấm máy tính
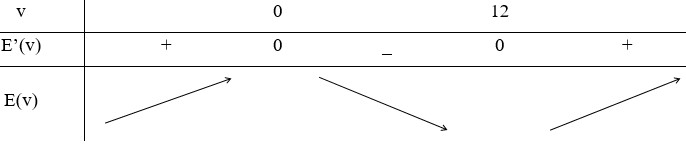
Đáp án D
h = 1 2 cos π t 8 + π 4 + 3 ≤ 1 2 + 3 = 7 2
Đẳng thức xảy ra khi cos π t 8 + π 4 = 1 ⇔ π t 8 + π 4 = k 2 π ⇔ t = 14 k
Do k ∈ ℤ và 0 h ≤ t ≤ 24 h nên k = 1 . Vậy
t = 14 h