Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Phương pháp: Sử dụng đạo hàm để tìm giá trị lớn nhất và giá trị nhỏ nhất.

Vậy có 1 số nguyên dương là 3 nằm giữa M và m

Đáp án D
f ' x = 2 cos x + 2 cos 2 x = 2 cos x + 4 cos 2 x − 2.
f ' x = 0 ⇔ cos x = − 1 cos x = 1 2 ⇔ x = π + k 2 π x = ± π 3 + k 2 π k ∈ ℤ .
=>M= 3 3 2 , m=0

Đáp án D.
Phương pháp
Phương pháp tìm GTLN, GTNN của hàm số y = f x trên [ a ; b ] .
+) Giải phương trình y ' = 0 ⇒ các nghiệm x i ∈ a ; b
+) Tính các giá trị f a ; f b ; f x i
+) So sánh và kết luận:
max a ; b f x = max f a ; f b ; f x i ; min a ; b f x = min f a ; f b ; f x i
Cách giải
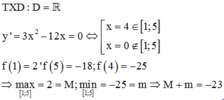

Đáp án D.
Phương pháp
Sử dụng tập giá trị của hàm y = sin x : 1 ≤ sin x ≤ 1 để đánh giá hàm số bài cho
Cách giải
Ta có:
− 1 ≤ s i n x ≤ 1 ⇒ − 1 ≤ − s i n x ≤ 1
2 − 1 ≤ 2 − s i n x ≤ 2 + 1 ⇔ 1 ≤ 2 − s i n x ≤ 3 ⇒ M = 3 ; m = 1

Chọn B.
Phương pháp
- Tính y' , tìm các nghiệm của y' = 0 .
- Tính giá trị của hàm số tại các điểm đầu mút và các điểm vừa tìm được ở bước trên và so sánh kết quả.
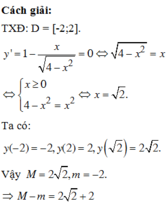

Đáp án B
Tập xác định: D = ℝ \ 1 2 ⇒ Hàm số y = m x + 1 2 x − 1 liên tục và đơn điệu trên 1 ; 3
⇒ a . b = y 1 . y 3 = m + 1 1 . 3 m + 1 5 = 1 5
⇔ m + 1 3 m + 1 = 1 ⇔ 3 m 2 + 4 m = 0 ⇔ m = 0 m = − 4 3
Vậy có 2 giá trị m thỏa mãn.

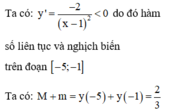
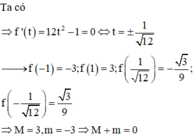

Đáp án B
Ta có y = 4 sin x − 3 cos x = 5 4 5 sinx − 3 5 cos x = 5 sin x − α với sin α = 3 5 cos α = 4 5
Ta có − 1 ≤ sin x − α ≤ 1 ⇒ − 5 ≤ 5 sin x − α ≤ 5 ⇒ M = 5 m = − 5