Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Vì hai vệ tinh cùng cách mặt đất 230 km nên tam giác AOB cân tại O.
Ta có: OA = R + 230
= 6370 + 230 = 6600 (km)
Trong tam giác AOB ta có: OH ⊥ AB
\(\Rightarrow\): HA = HB = AB/2 = 2200/2 = 1100 (km)
Áp dụng định lí Pi-ta-go vào tam giác vuông AHO, ta có:
OA2 = AH2 + OH2
\(\Rightarrow\): OH2 = OA2 – AH2
\(\Rightarrow\) :OH =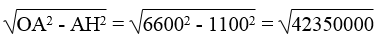 
≈ 6508 (km)
Vì OH > R nên hai vệ tinh nhìn thấy nhau.
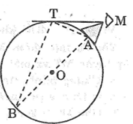
Điểm nhìn tối đa T là tiếp điểm của tiếp tuyến kẻ từ mắt đến bề mặt Trái Đất (như hình vẽ)
Xét hai tam giác MTA và MBT,ta có:
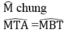
(hệ quả góc giữa tiếp tuyến và dây cung)
Suy ra ∆ MTA đồng dạng ∆ MBT
⇒ MT/MA = MB/MT => M T 2 = MA.MB
= MA (MA + 2R)
MA là chiều cao của đỉnh núi bằng 1km
Thay số ta có: M T 2 =1.(1 + 2.6400)=12801
Suy ra : MT ≈ 113,1(km)
Độ cao của máy bay là CD, độ dài AB = 80m
Gọi BC = x (x > 0) => AC = 80 + x
Xét tam giác BDC vuông tại C có CD = x . tan 55 0
Xét tam giác ADC vuông tại C có CD = (80 + x). tan 44 0
Suy ra x . tan 55 0 = (80 + x). tan 44 0
=> x ≈ 113,96m
=> CD = 113,96. tan 55 0 ≈ 162,75m
Vậy độ cao của máy bay so với mặt đất là 162,75m
Độ cao của máy bay là CD, độ dài AB = 60m; D A C ^ = 30 0 ; D B C ^ = 50 0
Gọi BC = x => AC = 60 + x
Xét tam giác BDC vuông tại C có:
Xét tam giác ADC vuông tại C có:
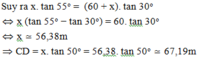
Vậy độ cao của máy bay so với mặt đất là 67,19m
Đáp án cần chọn là: C
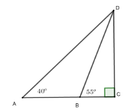
Độ cao của máy bay là CD, độ dài AB = 80m
Gọi BC = x (x > 0) => AC = 80 + x
Xét tam giác BDC vuông tại C có CD = x . tan 55 0
Xét tam giác ADC vuông tại C có CD = (80 + x). tan 44 0
Suy ra x . tan 55 0 = (80 + x). tan 44 0
=> x ≈ 113,96m
=> CD = 113,96. tan 55 0 ≈ 162,75m
Vậy độ cao của máy bay so với mặt đất là 162,75m
Đáp án cần chọn là: A
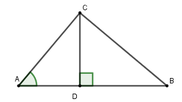
Độ cao của máy bay là CD, độ dài AB = 100m. Đào đứng ở A, Mai đứng ở B
Gọi AD = x (0 < x < 100) => BD = 150 – x
Xét ACD vuông tại D, ta có CD = AD.cot A = x . c o t 45 0 = x
Xét ABD vuông tại D, ta có CD = BD.cot B = (150 – x). c o t 35 0
Nên x = (150 – x). c o t 35 0 => x ≈ 88,22 (thỏa mãn)
=> CD = x = 88,22m
Vậy độ cao của diều lúc đó so với mặt đất là 88,22m
Đáp án cần chọn là: D
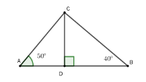
Độ cao của diều là CD, độ dài AB = 100m. Trung đứng ở A, Dũng đứng ở B
Gọi AD = x (0 < x < 100)
=> BD = 100 – x
Xét ACD vuông tại D, ta có CD = AD.tan A = x . tan 50 0
Xét ABD vuông tại D, ta có CD = BD.tan B = (100 – x). tan 40 0
Nên x . tan 50 0 = (100 – x). tan 40 0
Vậy độ cao của diều lúc đó so với mặt đất là 49,24m
Đáp án cần chọn là: B
- Áp dụng tỉ số lượng giác vào tam giác ABC vuông tại B
\(\Rightarrow tan60=\dfrac{h}{BC}\)
\(\Rightarrow BC=\dfrac{h\sqrt{3}}{3}\)
\(\Rightarrow BD=BC+CD=\dfrac{h\sqrt{3}}{3}+600\)
- Áp dụng tỉ số lượng giác vào tam giác ABD vuông tại B
\(tan50=\dfrac{h}{BD}\)
\(\Rightarrow h=tan50.\left(\dfrac{h\sqrt{3}}{3}+600\right)\)
\(\Rightarrow h\approx2292m\)
Vậy ...
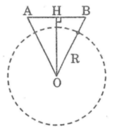
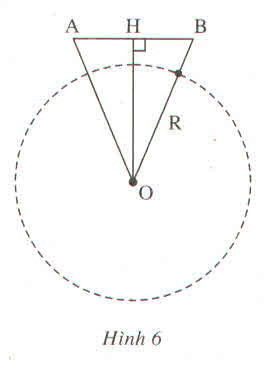
Vì hai vệ tinh cùng cách mặt đất 230 km nên tam giác AOB cân tại O.
Ta có: OA = R + 230
= 6370 + 230 = 6600 (km)
Trong tam giác AOB ta có: OH ⊥ AB
Suy ra: HA = HB = AB/2 = 2200/2 = 1100 (km)
Áp dụng định lí Pi-ta-go vào tam giác vuông AHO, ta có:
O A 2 = A H 2 + O H 2
Suy ra: O H 2 = O A 2 - A H 2
Suy ra:
OH =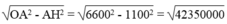
≈ 6508 (km)
Vì OH > R nên hai vệ tinh nhìn thấy nhau.