Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét 2 tam giác ABC và A’B’C có:
AB=A’B’ (gt)
\(\widehat A = \widehat {A'}\) (gt)
AC=A’C’ (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(c.g.c)

a) Xét ABD và EBD có
BD cạnh chung
BAD=BED(=90)
ABD=EBD(vì BD là tia phân giác của B)
b ko biet
b)Vì theo ý a) BAD=BED và BD là tia phân giác của B. Nên ADE là tam giác cân

a) Do tổng ba góc trong 1 tam giác bằng 180 độ nên tam giác không thể có 2 góc vuông
=> Tam giác vuông cân sẽ có 2 góc nhọn bằng nhau
=> Tam giác vuông cân thì cân tại đỉnh góc vuông.
b) Giả sử hai góc nhọn trong tam giác vuông là x, ta có:
\(\begin{array}{l}x + x + {90^o} = {180^o}\\ \Rightarrow 2x = {90^o}\\ \Rightarrow x = {45^o}\end{array}\)
Vậy tam giác vuông cân có hai góc nhọn bằng 45°.
c) Gọi góc còn lại của tam giác vuông có 1 góc nhọn bằng 45° là x, ta có:
\(x + {45^o} + {90^o} = {180^o} \Rightarrow x = {45^o}\)
Vậy tam giác vuông có một góc nhọn bằng 45° là tam giác vuông cân.

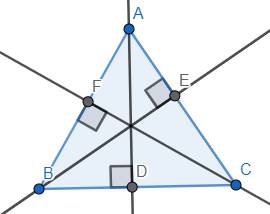
Nhận xét: AD, BE và CF là các đường cao, chúng đồng quy tại một điểm.
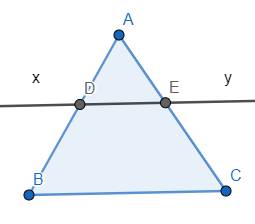
Dễ dàng thấy được \(\widehat{ABC}=\widehat{ADE}\) và \(\widehat{ACB}=\widehat{AED}\) (vì với mỗi cặp thì hai góc của cặp đó là hai góc so le trong)
Vì \(\widehat{ADE}\) và \(\widehat{BDE}\) là hai góc kề bù nên \(\widehat{ADE}+\widehat{BDE}=180^o\)
Mà \(\widehat{ABC}=\widehat{ADE}\) nên \(\widehat{ABC}+\widehat{BDE}=180^o\), suy ra \(\widehat{ABC}\) và \(\widehat{BDE}\) là hai góc bù nhau.
Suy luận tương tự như trên, ta được \(\widehat{ACB}\) và \(\widehat{CED}\) là hai góc bù nhau.

Ta có: C ^ = P ^ mà góc C và góc P là hai góc nhọn kề của tam giác ABC và tam giác MNP
Do đó để tam giác ABC và tam giác MNP bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề thì cần thêm điều kiện A C = M P
Đáp án A
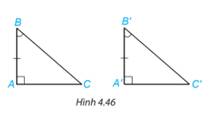
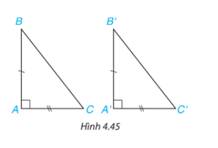
Xét 2 tam giác ABC và A'B'C' có:
\(\widehat B = \widehat {B'}\) (gt)
AB=A’B’ (gt)
\(\widehat A = \widehat {A'}\) (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(g.c.g)