Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Leftrightarrow y\left(sinx+2cosx+3\right)=sinx+cosx\)
\(\Leftrightarrow\left(y-1\right)sinx+\left(2y-1\right)cosx=-3y\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(\left(y-1\right)^2+\left(2y-1\right)^2\ge\left(-3y\right)^2\)
\(\Leftrightarrow4y^2+6y-2\le0\)
\(\Rightarrow M+m=\frac{-6}{2.4}=-\frac{3}{4}\)

\(M=2\cdot\left(1-cos^2x\right)-cosx+1\)
\(=-2\cdot cos^2x-cosx+1\)
\(=-2\cdot\left(cos^2x+\dfrac{1}{2}cosx-\dfrac{1}{2}\right)\)
\(=-2\cdot\left(cos^2x+2\cdot cosx\cdot\dfrac{1}{4}+\dfrac{1}{16}-\dfrac{9}{16}\right)\)
\(=-2\cdot\left(cosx+\dfrac{1}{4}\right)^2+\dfrac{9}{8}\)
-1<=cosx<=1
=>-3/4<=cosx+1/4<=5/4
=>0<=(cosx+1/4)^2<=25/16
=>0>=-2*cos(x+1/4)^2>=-25/8
=>9/8>=-2*cos(x+1/4)^2+9/8>=-25/8+9/8=-16/8=-2
=>M=9/8; m=-2
=>M+m=-7/8
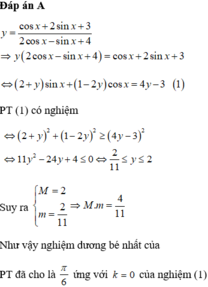
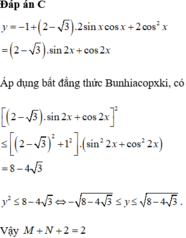
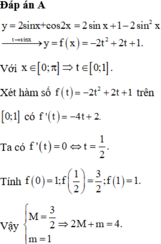
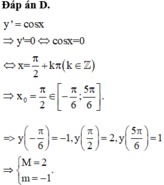

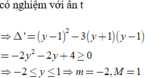
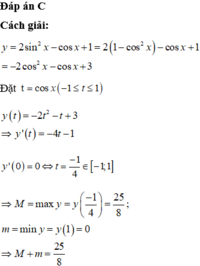
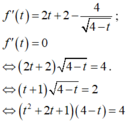
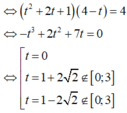
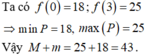


Chọn A