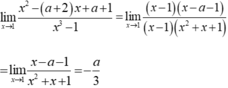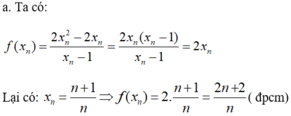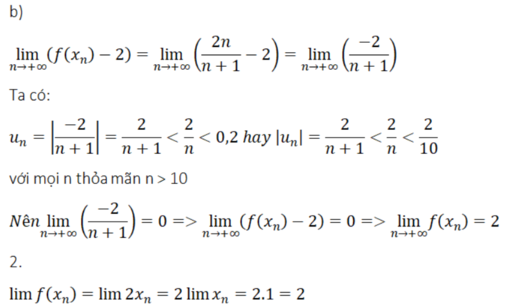Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

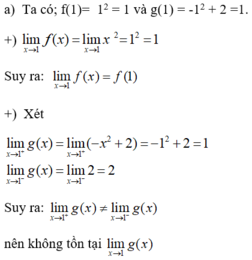
b)
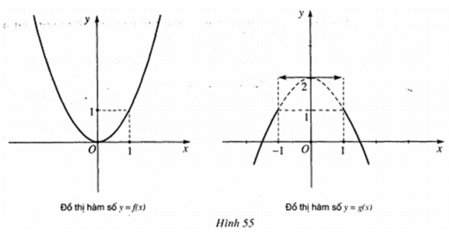
+ Đồ thị của hàm số y = f(x) là đường liền nét tại điểm có hoành độ x= 1.
+ Đồ thị hàm số y = g(x) là đường không liền nét tại điểm có hoành độ x= 1.

\(\lim\limits_{x\rightarrow1^-}x^2-x+3=1^2-1+3=3\)
\(\lim\limits_{x\rightarrow1^+}\dfrac{x+m}{x}=\dfrac{1+m}{1}=m+1\)
Để tồn tại \(\lim\limits_{x\rightarrow1}f\left(x\right)\) thì \(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)\)
\(\Leftrightarrow m+1=3\Leftrightarrow m=2\)
Vậy ...

\(\lim\limits_{x\rightarrow1^-}\dfrac{x^3-1}{x-1}=\lim\limits_{x\rightarrow1^-}\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x-1}=\lim\limits_{x\rightarrow1^-}x^2+x+1=1^2+1+1=3\)
\(\lim\limits_{x\rightarrow1^+}mx+2=\lim\limits_{x\rightarrow1^+}m+2\)
Để tồn tại \(\lim\limits_{x\rightarrow1}f\left(x\right)\) thì \(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\)
\(\Leftrightarrow m+2=3\\ \Leftrightarrow m=1\)
Vậy ...

Tại điểm x= -1 ta có:
lim x → − 1 − f ( x ) = lim x → − 1 − 3 x + b = − 3 + b = f ( − 1 ) lim x → − 1 + f x = lim x → − 1 + x + a = − 1 + a
Hàm số có giới hạn tại x= -1 khi và chỉ khi lim x → − 1 − f x = lim x → − 1 + f x
Điều này tương đương với − 3 + b = − 1 + a ⇒ a − b = − 2
Chọn đáp án B.

Ta có:
lim x → − 1 − h x = lim x → − 1 − x 3 + 1 x + 1 = lim x → − 1 − x 2 − x + 1 = 3 lim x → − 1 + h x = lim x → − 1 + m x 2 − x + m 2 = m + 1 + m 2
Hàm số có giới hạn tại x= -1 khi và chỉ khi lim x → − 1 − h x = lim x → − 1 + h x
3 = m + 1 + m 2 ⇔ m 2 + m − 2 = 0 ⇔ m = 1 m = − 2
Chọn đáp án C