K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BN
1
21 tháng 11 2018
học thuộc nhé bạn chứ không chứng minh đc nha -.-
ở lớp 8 chúng ta sẽ học 7 hằng đẳng thức đáng nhớ nhé !!!
1. Bình phương của một tổng : (a + b)2 = a2 + 2.a.b + b2
2. Bình phương của một hiệu : (a - b)2 = a2 - 2.a.b + b2
3. Hiệu hai bình phương : a2 - b2 = (a - b).(a + b)
4. Lập phương của một tổng : (a + b)3 = a3 + 3.a2.b + 3.a.b2 + b3
5. Lập phương của một hiệu : (a - b)3 = a3 - 3.a2.b + 3.a.b2 - b3
6. Tổng hai lập phương : a3 + b3 = (a + b).(a2 - a.b + b2)
7. Hiệu hai lập phương : a3 - b3 = (a - b).(a2 + a.b +b2)
18 tháng 5 2017
\(M\left(x\right)=x^2-2x+1=x^2-x-x+1\)
\(=x\left(x-1\right)-\left(x-1\right)=\left(x-1\right)\left(x-1\right)\)
\(=\left(x-1\right)^2\)
Ta có: \(\left(x-1\right)^2=0\Rightarrow x-1=0\Rightarrow x=1\)
Vậy x = 1 là nghiệm của M(x)
26 tháng 4 2018
F(x) = 2x5 + 3x3 - 4x4 + 5x - x2 + x3 + x1
F(x) = 2x5 -4x4 + ( 3x3 + x3 ) -x2 + ( 5x+x)
F(x) = 2x5 - 4x4 + 4x3 - x2 + 6x
G(x) = -x2 - x5 + 2x4 - 3x3 + x4 +7
G(x) = -x5 + ( 2x4 + x4) -x2 +7
G ( x) = -x5 + 3x4 -x2 +7
26 tháng 4 2018
a,F(x)= 2x\(^5\) + 3x\(^3\) - 4x\(^4\) + 5x - x\(^2\) + x\(^3\) + x\(^1\)
=2x\(^5\)- 4x\(^4\) \(+4x^3\)\(-x^2+6x\)
G(x)= -x\(^2\) - x\(^5\) + 2x\(^4\) - 3x\(^3\) + x\(^4\) + 7
=\(-x^5\)\(+3x^4\)\(-3x^3\)\(-x^2\)+7
b,F(x)-G(x)=(2x\(^5\)- 4x\(^4\) \(+4x^3\)\(-x^2+6x\))-\((-x^5+3x^4-3x^3-x^2+7)\)
=\(2x^5-4x^4+4x^3-x^2+6x\) \(+x^5-3x^4\)\(+3x^3\)\(+x^2-7\)
=\(\left(2x^5+x^5\right)\)+\(\left(-4x^4-3x^4\right)\)+\(\left(4x^3+3x^3\right)\)\(\left(-x^2+x^2\right)\)+6x-7
=\(3x^5-7x^4\)\(+7x^3+6x-7\)
H9
HT.Phong (9A5)
CTVHS
7 tháng 11 2023
a)
\(0,3-\dfrac{8}{3}:\dfrac{4}{3}\cdot\dfrac{1}{5}+1\\ =\dfrac{3}{10}-\dfrac{8}{3}\cdot\dfrac{3}{4}\cdot\dfrac{1}{5}+1\\ =\dfrac{3}{10}-2\cdot\dfrac{1}{5}+1\\ =\dfrac{3}{10}-\dfrac{2}{5}+1\\ =\dfrac{9}{10}\)
b)
\(\left(-\dfrac{1}{2}\right)^2-\dfrac{5}{8}:\left(0,5\right)^3-\dfrac{5}{3}\cdot\left(-6\right)\\ =\dfrac{1}{4}-\dfrac{5}{8}:\dfrac{1}{8}+\dfrac{5}{3}\cdot6\\ =\dfrac{1}{4}-\dfrac{5}{8}\cdot8+10\\ =\dfrac{1}{4}-5+10\\ =\dfrac{21}{4}\)
c)
\(2+4:\left(\dfrac{2}{3}-\dfrac{1}{6}\right)\cdot\left(-2,25\right)\\ =2+4:\dfrac{1}{2}\cdot\left(-2,25\right)\\ =2+8\cdot\left(-2,25\right)\\ =2-18\\ =-16\)
d)
\(\left(2\dfrac{5}{6}+1\dfrac{4}{9}\right):\left(10\dfrac{1}{12}-9\dfrac{1}{2}\right)\\ =\left(2+\dfrac{5}{6}+1+\dfrac{4}{9}\right):\left(10+\dfrac{1}{12}-9-\dfrac{1}{2}\right)\\ =\left(3+\dfrac{23}{18}\right):\left(1-\dfrac{5}{12}\right)\\ =\dfrac{77}{18}:\dfrac{7}{12}\\ =\dfrac{22}{3}\)
11 tháng 10 2021
\(\left|\dfrac{1}{3}+2019x\right|+\left|\dfrac{2}{3}+2020x\right|=4040x\left(đk:x\ge0\right)\)
\(\Rightarrow\dfrac{1}{3}+2019x+\dfrac{2}{3}+2020x=4040x\)
\(\Rightarrow x=1\left(tm\right)\)
AM
3 tháng 10 2017
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{y+z+1}{x}=\dfrac{x+z+2}{y}=\dfrac{x+y-3}{z}=\dfrac{x+y+1+x+z+2+x+y-3}{x+y+z}=\dfrac{\left(x+y+z\right)+\left(x+y+z\right)+\left(1+2-3\right)}{x+y+z}=\dfrac{2.\left(x+y+z\right)}{x+y+z}=2\)
Lại có:
\(\dfrac{y+z+1}{x}+\dfrac{x+z+2}{y}+\dfrac{x+y-3}{z}=\dfrac{1}{x+y+z}\)
\(\Rightarrow2=\dfrac{1}{x+y+z}\)
\(\Rightarrow2.\left(x+y+z\right)=1\)
\(\Rightarrow x+y+z=\dfrac{1}{2}\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{y+z+1}{x}=2\\\dfrac{x+z+2}{y}=2\\\dfrac{x+y-3}{z}=2\\x+y+z=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}y+z+1=2x\\x+z+2=2y\\x+y-3=2z\\x+y+z=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+y+z+1=3x\\x+y+z+2=3y\\x+y+z-3=3z\\x+y+z=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\dfrac{1}{2}+1=3x\\\dfrac{1}{2}+2=3y\\\dfrac{1}{2}-3=3z\\x+y+z=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1+\dfrac{1}{2}}{3}\\y=\dfrac{\dfrac{1}{2}+2}{3}\\z=\dfrac{\dfrac{1}{2}-3}{3}\\x+y+z=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{5}{6}\\z=-\dfrac{5}{6}\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{5}{6}\\z=-\dfrac{5}{6}\end{matrix}\right.\) .
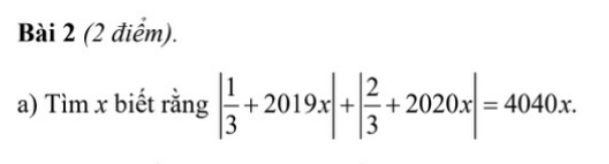
\(A=\left(4x^7y^5-4x^7y^5\right)+2xy^2-4y^2+2019\)
\(=2xy^2-4y^2+2019\)
\(=2\cdot2\cdot9-4\cdot9+2019=2019\)