K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 2 2017
XÉT TAM GIÁC ABH VÀ ACH CÓ
AH CHUNG
GÓC AHB= GÓC AHC
GÓC B=GÓC C
=>TAM GIÁC ABH = TAM GIÁC ACH (CH-GN)
QC
13 tháng 1 2020
a) Xét ΔDAN,ΔHANΔDAN,ΔHAN có :
HN=ND(gt)HN=ND(gt)
ANDˆ=ANHˆ(=90O)AND^=ANH^(=90O)
AN:ChungAN:Chung
=> ΔDAN=ΔHAN(c.g.c)ΔDAN=ΔHAN(c.g.c)
b) Xét ΔAMH,ΔAMEΔAMH,ΔAME có :
HM=ME(gt)HM=ME(gt)
AMHˆ=AMEˆ(=90o)AMH^=AME^(=90o)
AM:ChungAM:Chung
=> ΔAMH=ΔAME(c.g.c)ΔAMH=ΔAME(c.g.c)
Xét tứ giác ANHM có :
Nˆ=90O(HN⊥AB)N^=90O(HN⊥AB)
Aˆ=90O(ΔABC⊥A)A^=90O(ΔABC⊥A)
Mˆ=90O(HM⊥AC)M^=90O(HM⊥AC)
=> Tứ giác ANHM là hình chữ nhật
=> {NH=AMNA=HM{NH=AMNA=HM (tính chất hình chữ nhật)
Ta dễ dàng chứng minh được : ΔANH=ΔAMH(c.c.c)ΔANH=ΔAMH(c.c.c)
Mà : {ΔAND=ΔANHΔAHM=ΔAEM(cmt){ΔAND=ΔANHΔAHM=ΔAEM(cmt)
Suy ra : ΔAND=ΔAMEΔAND=ΔAME
=> DA=AEDA=AE(2 cạnh tương ứng) (*)
c) Từ (*) => A là trung điểm của DE
Do đó : D,A,E thẳng hàng (đpcm)
5 tháng 9 2019
Kéo dài MN cắt AC tại F
Ta có: \(\hept{\begin{cases}AB//NF\\AB\perp AC\end{cases}\Rightarrow NF\perp}AC\)
Xét tam giác ACN có:
\(\hept{\begin{cases}NF\perp AC\left(cmt\right)\\AH\perp NC\left(gt\right)\end{cases}}\)
Mà M là giao điểm của NF và AH
\(\Rightarrow M\)là trực tâm của tam giác ACN
\(\Rightarrow EC\perp AN\)( tc )
\(\Rightarrow\widehat{AEC}=90^0\)
\(\Rightarrow\Delta AEC\)vuông tại E
KK
23 tháng 3 2022
a)
Áp dụng định lý pitago vào tam giác vuông ABC, có:
BC2=AB2+AC2BC2=AB2+AC2
⇒BC=√62+82=√100=10cm⇒BC=62+82=100=10cm
b.Xét tam giác vuông ABH và tam giác vuông ADH, có:
HD = HB ( gt )
AH: cạnh chung
Vậy tam giác vuông ABH = tam giác vuông ADH ( 2 cạnh góc vuông )
=> AB = AD ( 2 cạnh tương ứng )
bn tham khảo
23 tháng 3 2022
a,Áp dụng Đ. L. py-ta-go, có:
BC2=AC2+AB2
=>BC2=82+62
=64+36.
=100.
=>BC=10cm.
b, Xét tg AHB và tg AHD, có:
AH chung
góc AHB= góc AHD(=90o)
HB= DH(gt)
=>tg AHB= tg AHD(2 cạnh góc vuông)
=>AB= AD(2 cạnh tương ứng)
c, Kẻ E với C, tạo thành cạnh EC.
Kẻ E với B, tạo thành cạnh EB.
Ta có: góc BHA=90o, suy ra: góc BHA= góc EHC(2 góc đối đỉnh)
=>góc BHA= góc EHC(=90o)
=>ED vuông góc với AC(đpcm)
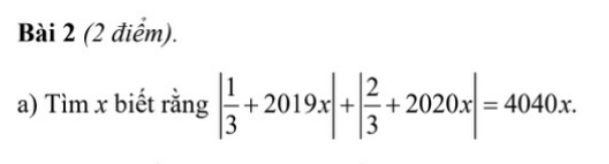
\(\left|\dfrac{1}{3}+2019x\right|+\left|\dfrac{2}{3}+2020x\right|=4040x\left(đk:x\ge0\right)\)
\(\Rightarrow\dfrac{1}{3}+2019x+\dfrac{2}{3}+2020x=4040x\)
\(\Rightarrow x=1\left(tm\right)\)
Đg định mần thì........ :(