K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
31 tháng 10 2021
a: Để (d)//y=x-3 thì \(4-m^2=1\)
\(\Leftrightarrow m\in\left\{\sqrt{3};-\sqrt{3}\right\}\)
16 tháng 12 2021
a: Thay x=16 vào B, ta được:
\(B=\dfrac{4+3}{4-2}=\dfrac{7}{2}\)
25 tháng 10 2021
\(M=\sqrt{\dfrac{\left(11+\sqrt{96}\right)^2}{121-96}}+\sqrt{\dfrac{\left(11-\sqrt{96}\right)^2}{121-96}}\\ M=\dfrac{11+\sqrt{96}}{5}+\dfrac{11-\sqrt{96}}{5}=\dfrac{22}{5}\)
25 tháng 10 2021
\(K=\left(\sqrt{5}-\sqrt{3}\right)\cdot\sqrt{2}\cdot\sqrt{4-\sqrt{15}}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)\)
\(=8-2\sqrt{15}\)
26 tháng 2 2022
\(a)\) Thay \(m=6\) vào phương trình (1), ta có:
\(x^2+x-6=0.\\ \Delta=1^2-4.1.\left(-6\right).\\ \Delta=25>0.\)
\(\Rightarrow\) Phương trình có 2 nghiệm phân biệt.
\(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{-1+\sqrt{25}}{2.1}=\dfrac{-1+5}{2}=2.\\x_2=\dfrac{-1-\sqrt{25}}{2.1}=\dfrac{-1-5}{2}=-3.\end{matrix}\right.\)
\(b)\) Để phương trình (1) có 2 nghiệm phân biệt.
\(\Leftrightarrow\Delta>0\\ .\Leftrightarrow1^2-4.1.\left(-m\right)>0.\\ \Leftrightarrow1+4m>0.\\ \Leftrightarrow4m>-1.\\ \Leftrightarrow m>\dfrac{-1}{4}.\)
11 tháng 3 2022
Bài 2
a, bạn tự vẽ
b, Hoành độ giao điểm tm pt
\(2x^2-2x+3=0\)
\(\Delta'=1-3.2=-5< 0\)
Vậy pt vô nghiệm hay (d) ko cắt (P)
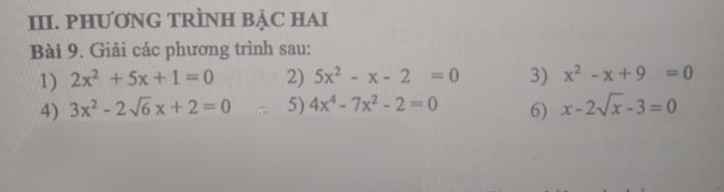
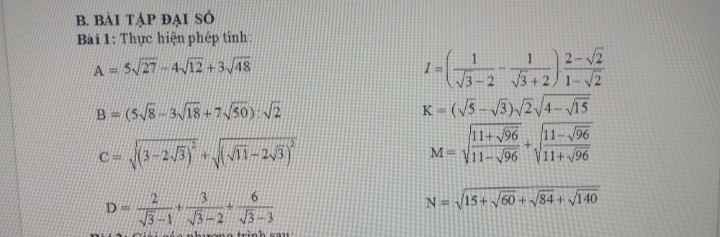
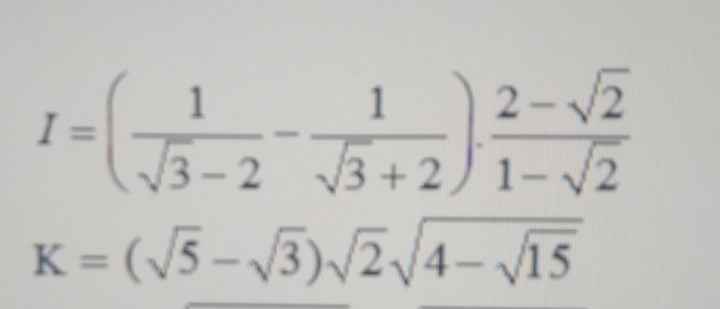
\(1,\Delta=b^2-4ac=5^2-4.2=17>0\)
=> Pt có 2n pb
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-5+\sqrt{17}}{4}\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-5-\sqrt{17}}{4}\)
2,\(\Delta=b^2-4ac=\left(-1\right)^2-4.5.\left(-2\right)=41>0\)
=> Pt có 2n pb
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{1+\sqrt{41}}{10}\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{1-\sqrt{41}}{10}\)