K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
16 tháng 12 2021
a: Thay x=16 vào B, ta được:
\(B=\dfrac{4+3}{4-2}=\dfrac{7}{2}\)
31 tháng 10 2021
a: Để (d)//y=x-3 thì \(4-m^2=1\)
\(\Leftrightarrow m\in\left\{\sqrt{3};-\sqrt{3}\right\}\)
26 tháng 10 2021
\(M=\sqrt{\dfrac{11+\sqrt{96}}{11-\sqrt{96}}}+\sqrt{\dfrac{11-\sqrt{96}}{11+\sqrt{96}}}\)
\(\Rightarrow M=\sqrt{\dfrac{\left(11+\sqrt{96}\right)^2}{121-96}}+\sqrt{\dfrac{\left(11-\sqrt{96}\right)^2}{121-96}}\)
\(\Rightarrow M=\sqrt{\dfrac{\left(11+\sqrt{96}\right)^2}{25}}+\sqrt{\dfrac{\left(11-\sqrt{96}\right)^2}{25}}\)
\(\Rightarrow M=\dfrac{11+\sqrt{96}}{5}+\dfrac{11-\sqrt{96}}{5}\)
\(\Rightarrow M=\dfrac{22}{5}\)
26 tháng 10 2021
\(N=\sqrt{15+2\sqrt{15}+2\sqrt{21}+2\sqrt{35}}\\ N=\sqrt{3+5+7+2\sqrt{3}\sqrt{5}+2\sqrt{3}\sqrt{7}+2\sqrt{5}\sqrt{7}}\\ N=\sqrt{\left(\sqrt{3}+\sqrt{5}+\sqrt{7}\right)^2}=\sqrt{3}+\sqrt{5}+\sqrt{7}\)
16 tháng 3 2022
\(\text{Δ}=\left(-2m\right)^2-4\left(m^2-m-2\right)\)
\(=4m^2-4m^2+4m+8\)
=4m+8
Để phương trình có hai nghiệm thì 4m+8>=0
hay m>=-2
Theo đề, ta có: \(\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow\left(-2m\right)^2-2\left(m^2-m-2\right)=4\)
\(\Leftrightarrow4m^2-2m^2+2m=0\)
=>2m(m+1)=0
=>m=0 hoặc m=-1
Y
6 tháng 3 2022
\(1,\Delta=b^2-4ac=5^2-4.2=17>0\)
=> Pt có 2n pb
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-5+\sqrt{17}}{4}\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-5-\sqrt{17}}{4}\)
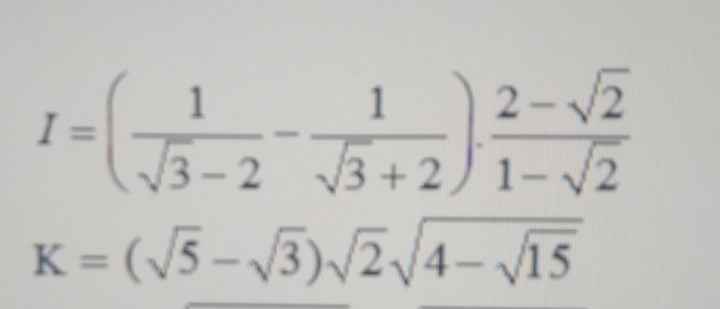
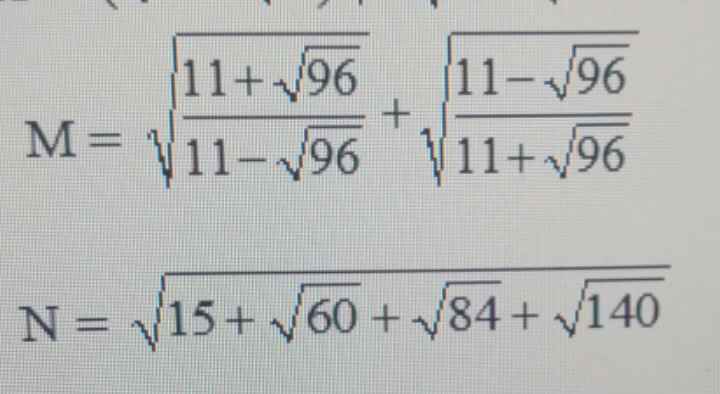
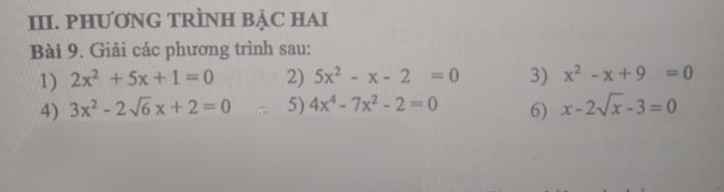
\(K=\left(\sqrt{5}-\sqrt{3}\right)\cdot\sqrt{2}\cdot\sqrt{4-\sqrt{15}}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)\)
\(=8-2\sqrt{15}\)