K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 12 2021
a, \(\dfrac{\sqrt{80}}{\sqrt{5}}\)-\(\sqrt{5}\).\(\sqrt{20}\)= \(\sqrt{16}\)-10=-6
b, (\(\sqrt{28}\)-\(\sqrt{12}\)-\(\sqrt{7}\))\(\sqrt{7}\)+2\(\sqrt{21}\)=\(\sqrt{196}\)-\(\sqrt{84}\)-7+2 \(\sqrt{21}\)=14-7=7
c, \(\sqrt[3]{2}\).\(\sqrt[3]{32}\)+\(\sqrt{2}\).\(\sqrt{32}\)=\(\sqrt[3]{64}\)+\(\sqrt{64}\)=4+8=12
d, \(2\sqrt{8\sqrt{3}}\)-\(\sqrt{2\sqrt{3}}\)-\(\sqrt{9\sqrt{12}}\)=\(4\sqrt{12}\)-\(\sqrt{12}\)-\(3\sqrt{12}\)=0
12 tháng 1
1: \(x^2-\left(m+1\right)x-2023=0\)
a=1; b=-(m+1); c=-2023
Vì \(a\cdot c=-2023< 0\)
nên phương trình luôn có hai nghiệm phân biệt
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-\left[-\left(m+1\right)\right]}{1}=m+1\\x_2\cdot x_1=\dfrac{c}{a}=-\dfrac{2023}{1}=-2023\end{matrix}\right.\)
\(\dfrac{1}{x_1-2023}+\dfrac{1}{x_2-2023}=1\)
=>\(\dfrac{x_2-2023+x_1-2023}{\left(x_1-2023\right)\left(x_2-2023\right)}=1\)
=>\(x_2+x_1-4046=\left(x_1-2023\right)\left(x_2-2023\right)\)
=>\(m+1-4046=x_1x_2-2023\left(x_1+x_2\right)+2023^2\)
=>\(m-4045=-2023-2023\left(m+1\right)+2023^2\)
=>\(m-4045=-2023-2023m-2023+2023^2\)
=>\(2024m=4092528\)
=>\(m=\dfrac{4092528}{2024}=2022\)
AT
16 tháng 7 2021
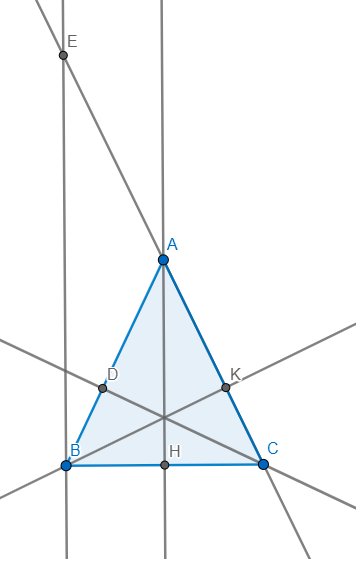
b) Từ B kẻ đường vuông góc với BC cắt AC tại E
tam giác BEC vuông tại B có \(AB=AC\Rightarrow A\) là trung điểm CE
Vì tam giác ABC cân tại A có AH là đường cao \(\Rightarrow H\) là trung điểm BC
\(\Rightarrow AH\) là đường trung bình tam giác BEC
\(\Rightarrow AH=\dfrac{1}{2}BE\Rightarrow2AH=BE\Rightarrow4AH^2=BE^2\)
tam giác BEC vuông tại B có BK là đường cao \(\Rightarrow\dfrac{1}{BE^2}+\dfrac{1}{BC^2}=\dfrac{1}{BK^2}\)
\(\Rightarrow\dfrac{1}{4AH^2}+\dfrac{1}{BC^2}=\dfrac{1}{BK^2}\)
ND
0
ND
0
10 tháng 7 2023
2:
a: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
b: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AB*AE
c: góc ABF=góc ACF=1/2*sđ cung AF=90 độ
=>BF//CH và CF//BH
=>BFCH là hình bình hành
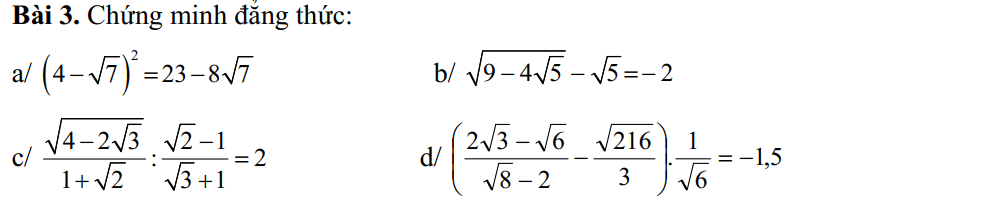
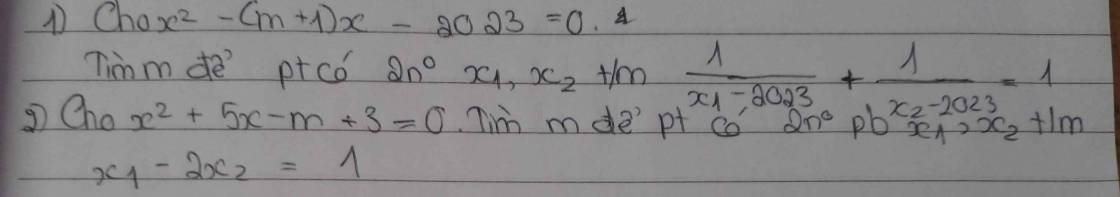
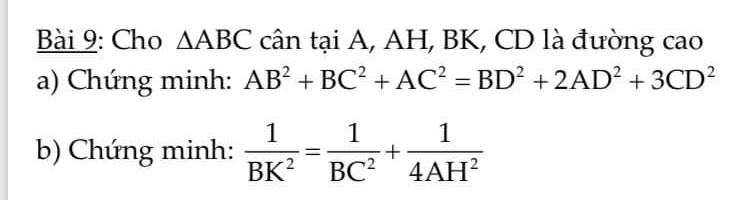
b: \(=\sqrt{5}-2-\sqrt{5}=-2\)