K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BM
3
19 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
`8,`
`a,`
Thay \(x=18;y=41\) vào bt
\(18^2-4\cdot41^2\)
`= 18^2 - (2*41)^2`
`= 18^2 - 82^2`
`= -6400`
`b,`
\(87^2+13^2+26\cdot87\)
`= 87*(87+26) + 169`
`= 87*113 + 169`
`= 9831 + 169`
`= 10000`
Y
19 tháng 6 2023
\(9,\) \(a,\left(2x+1\right)^2-4\left(x-1\right)\left(x+1\right)=2x-4\)
\(\Leftrightarrow4x^2+4x+1-4\left(x^2-1\right)-2x+4=0\)
\(\Leftrightarrow4x^2+4x+1-4x^2+4-2x+4=0\)
\(\Leftrightarrow\left(4x^2-4x^2\right)+\left(4x-2x\right)+\left(1+4+4\right)=0\)
\(\Leftrightarrow2x=-9\)
\(\Leftrightarrow x=-\dfrac{9}{2}\)
Vậy \(S=\left\{-\dfrac{9}{2}\right\}\)
\(b,\left(-3+x\right)^2-2\left(2-x\right)\left(x+2\right)-3\left(x+1\right)^2=4\)
\(\Leftrightarrow9-6x+x^2-2\left(2x+4-x^2-2x\right)-3\left(x^2+2x+1\right)-4=0\)
\(\Leftrightarrow9-6x+x^2-4x-8+2x^2+4x-3x^2-6x-3-4=0\)
\(\Leftrightarrow-12x=6\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy \(S=\left\{-\dfrac{1}{2}\right\}\)
\(c,3x^2+\left(-1-x\right)^2=\left(2x+5\right)\left(2x-5\right)\)
\(\Leftrightarrow3x^2+1+2x+x^2=4x^2-25\)
\(\Leftrightarrow2x=-26\)
\(\Leftrightarrow x=-13\)
Vậy \(S=\left\{-13\right\}\)
17 tháng 6 2016
A = n2(n + 1) + 2n(n+1) = n(n+1)(n+2)
Ta thấy A là tích của 3 số tự nhiên liên tiếp nên nó chia hết cho 3
Và n(n+1) luôn chia hết cho 2 vì là tích của 2 số tự nhiên liên tiếp nên A chia hết cho 2.
Số A vừa chia hết cho 2 vừa chia hết cho 3 nên A chia hết cho 2*3 = 6 . ĐPCM
17 tháng 6 2016
Đinh Thùy Linh Bạn cần bổ sung thêm nữa :
\(\left(2,3\right)=1\)
14 tháng 8 2023
14:
a: \(A=\dfrac{15x^5y^3-10x^3y^2+20x^4y^4}{5x^2y^2}\)
\(=\dfrac{5x^2y^2\left(3x^3y-10x+4x^2y^2\right)}{5x^2y^2}=3x^3y-10x+4x^2y^2\)
Khi x=-1 và y=2 thì \(A=3\left(-1\right)^3\cdot2-10\cdot\left(-1\right)+4\cdot\left(-1\cdot2\right)^2\)
\(=-6+10+4\cdot4=4+16=20\)
b: \(B=\dfrac{4x^4y^2+3x^4y^3-6x^3y^2}{x^2y^2}=4x^2+3x^2y-6x\)
Khi x=y=-2 thì \(B=4\cdot\left(-2\right)^2+3\cdot\left(-2\right)^2\left(-2\right)-6\left(-2\right)\)
\(=16+12-6\cdot4=28-24=4\)
c: \(C=\dfrac{\dfrac{2}{3}xy\left(-3xy+6-9y^2\right)}{\dfrac{2}{3}xy}=-3xy+6-9y^2\)
Khi x=1/2 và y=4 thì \(C=-3\cdot\dfrac{1}{2}\cdot4+6-9\cdot4^2\)
=-6+6-9*16
=-144
d: \(D=\dfrac{x^2y^2\left(\dfrac{1}{3}y^3-\dfrac{2}{3}x^3\right)}{2x^2y^2}=\dfrac{1}{6}y^3-\dfrac{1}{3}x^3\)
Khi x=-3 và y=3 thì \(D=\dfrac{-1}{3}\left(-3\right)^3-\dfrac{1}{6}\cdot3^3\)
=9-9/2
=9/2
e: \(E=\dfrac{5x^2y\left(4x^3y^3+2xy-y^2\right)}{5x^2y}=4x^3y^3+2xy-y^2\)
Khi x=1 và y=-1 thì \(E=-4-2-1=-7\)
f: G\(=\dfrac{x^2yz\left(7x^3y^3z^2-3x^2z+2y\right)}{x^2yz}=7x^3y^3z^2-3x^2z+2y\)
Khi x=-1;y=1;z=2 thì \(G=7\cdot\left(-1\cdot1\right)^3\cdot2^2-3\cdot\left(-1\right)^2\cdot2+2\cdot1\)
=-7*4-6+2
=-28-4=-32
Y
19 tháng 6 2023
\(7,\) \(a,\left(2x-3y\right)^2-\left(2x+3y\right)^2=\left(3x-2y\right)^2-\left(3x+2y\right)^2\)
\(\Leftrightarrow4x^2-12xy+9y^2-4x^2-12xy-9y^2=9x^2-12xy+4y^2-9x^2-12xy-4y^2\)
\(\Leftrightarrow-24xy=-24xy\) ( luôn đúng )
Vậy 2 đẳng thức ở 2 vế bằng nhau.
\(b,\left(a^2+b^2\right)\left(c^2+d^2\right)=\left(ac+bd\right)^2+\left(ad-bc\right)^2\)
\(\Leftrightarrow\left(ac\right)^2+\left(ad\right)^2+\left(bc\right)^2+\left(bd\right)^2=\left(ac\right)^2+2acbd+\left(bd\right)^2+\left(ad\right)^2-2adbc+\left(bc\right)^2\)
\(\Leftrightarrow\left(ac\right)^2+\left(ad\right)^2+\left(bc\right)^2+\left(bd\right)^2=\left(ac\right)^2+\left(ad\right)^2+\left(bc\right)^2+\left(bd\right)^2\) ( luôn đúng )
Vậy 2 đẳng thức ở 2 vế bằng nhau.
*Ở câu \(b,\) dòng thứ 3, vế phải triệt tiêu \(2acbd-2adbc\) \(=0\) nên mất rồi nha.
25 tháng 7 2018
a) Đặt \(A=-x^2+9x-12\)
\(-A=x^2-9x+12\)
\(-A=\left(x^2-9x+\frac{81}{4}\right)-\frac{33}{4}\)
\(-A=\left(x-\frac{9}{2}\right)^2-\frac{33}{4}\)
Mà \(\left(x-\frac{9}{2}\right)^2\ge0\forall x\)
\(\Rightarrow-A\ge-\frac{33}{4}\Leftrightarrow A\le\frac{33}{4}\)
Dấu "=" xảy ra khi : \(x-\frac{9}{2}=0\Leftrightarrow x=\frac{9}{2}\)
Vậy \(A_{Max}=\frac{33}{4}\Leftrightarrow x=\frac{9}{2}\)
b) Đặt \(B=2x^2+10x-1\)
\(B=2\left(x^2+5x+\frac{25}{4}\right)-\frac{29}{4}\)
\(B=2\left(x+\frac{5}{2}\right)^2-\frac{29}{4}\)
Mà \(\left(x+\frac{5}{2}\right)^2\ge0\forall x\Rightarrow2\left(x+\frac{5}{2}\right)^2\ge0\forall x\)
\(\Rightarrow B\ge-\frac{29}{4}\)
Dấu "=" xảy ra khi : \(x+\frac{5}{2}=0\Leftrightarrow x=-\frac{5}{2}\)
Vậy \(B_{Min}=-\frac{29}{4}\Leftrightarrow x=-\frac{5}{2}\)
25 tháng 7 2018
c) Đặt \(C=\left(2x+6\right)\left(x-1\right)\)
\(C=2x^2-2x+6x-6\)
\(C=2x^2+4x-6\)
\(C=2\left(x^2+2x+1\right)-8\)
\(C=2\left(x+1\right)^2-8\)
Mà \(\left(x+1\right)^2\ge0\forall x\Rightarrow2\left(x+1\right)^2\ge0\forall x\)
\(\Rightarrow C\ge-8\)
Dấu "=" xảy ra khi : \(x+1=0\Leftrightarrow x=-1\)
Vậy \(C_{Min}=-8\Leftrightarrow x=-1\)
d) Đặt \(D=3x-2x^2\)
\(-2D=4x^2-6x\)
\(-2D=\left(4x^2-6x+\frac{9}{4}\right)-\frac{9}{4}\)
\(-2D=\left(2x-\frac{3}{2}\right)^2-\frac{9}{4}\)
Mà \(\left(2x-\frac{3}{2}\right)^2\ge0\forall x\)
\(\Rightarrow-2D\ge-\frac{9}{4}\)
\(\Leftrightarrow D\le\frac{9}{8}\)
Dấu "=" xảy ra khi : \(2x-\frac{3}{2}=0\Leftrightarrow x=\frac{3}{4}\)
Vậy \(D_{Max}=\frac{9}{8}\Leftrightarrow x=\frac{3}{4}\)
MA
1
22 tháng 5 2021
Bài 1:
b) \(B=A.\dfrac{-10}{x-4}=\dfrac{x-4}{x+5}.\dfrac{-10}{x-4}=\dfrac{-10}{x+5}\)
Để B nguyên <=> x+5 nguyên mà \(x\in Z\Rightarrow x+5\inƯ\left(-10\right)=\left\{\pm1;\pm2;\pm5;\pm10\right\}\)
\(\Leftrightarrow x\in\left\{-6;-4;-3;-7;0;-10;-15;5\right\}\) kết hợp với điều kiện của x
\(\Rightarrow x\in\left\{-15;-10;-6;-7;-3;0;5\right\}\)
Bài 5:
Có \(\left|x-2018\right|+\left|2x-2019\right|+\left|3x-2020\right|\ge0\) \(\forall\)x
\(\Rightarrow x-2021\ge0\) \(\Leftrightarrow x\ge2021\)
\(\Rightarrow x-2018>0,2x-2019>0,3x-2020>0\)
PT \(\Leftrightarrow x-2018+2x-2019+3x-2020=x-2021\)
\(\Leftrightarrow5x=4036\) \(\Leftrightarrow x=\dfrac{4036}{5}< 2021\) (L)
Vậy pt vô nghiệm
4 tháng 8 2023
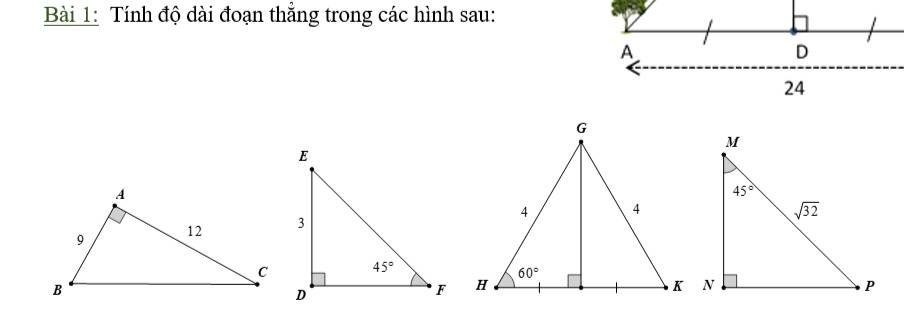
3: ΔGHK cân tại G có góc H=60 độ
nên ΔGHK đều
=>HK=GH=4
4: Xét ΔMNP vuông tại N có góc M=45 độ
nên ΔMNP vuông cân tại N
=>\(NP=NM=\sqrt{\dfrac{MP^2}{2}}=4\left(cm\right)\)
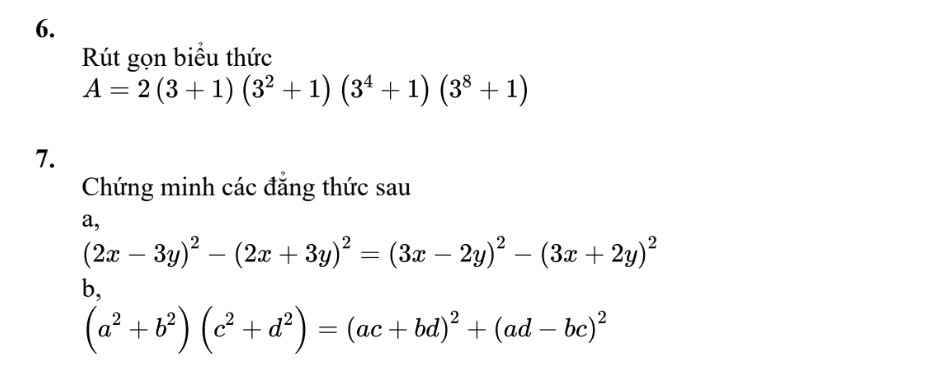
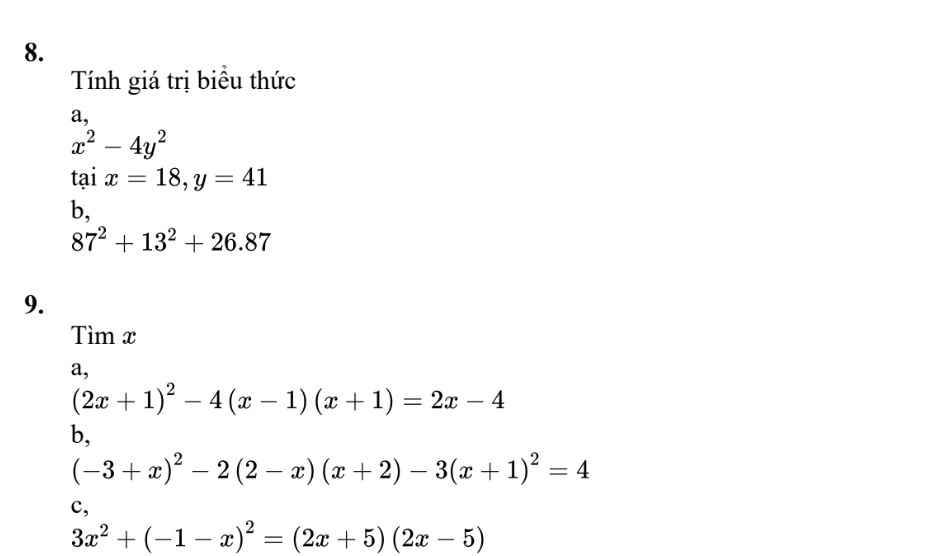
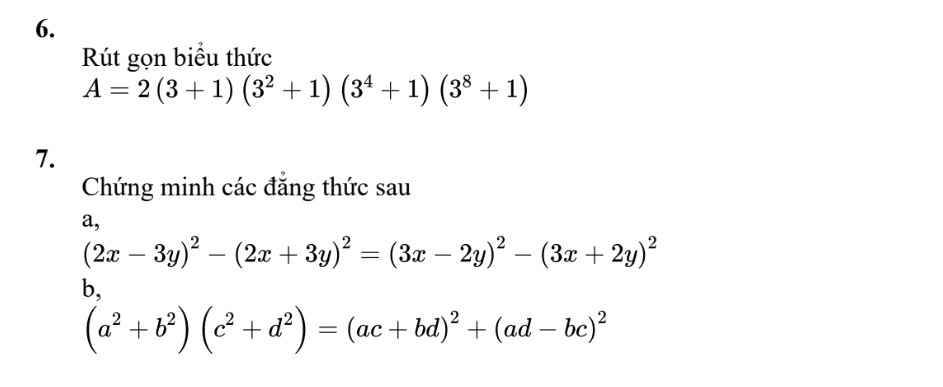
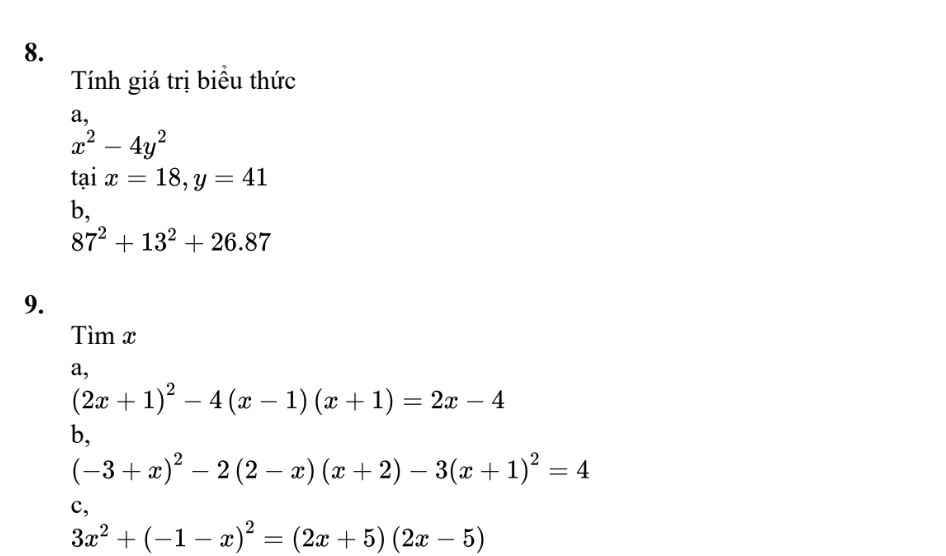
2:
a: A={x∈N|1<=x<=5}
b: B={x∈N|x<=4}
c: C={x∈N*|x<=4}
d: D={x∈N|x chia hết 2; x<10}
e: E={x∈N|x ko chia hết cho 2; x<50}
f: F={x∈N|x chia hết cho 11; x<100}
3:
a: A={4}
=>Có 1 phần tử
b: B={0;1}
=>Có 2 phần tử
c: C=∅
=>Ko có phần tử
d: D={0}
=>Có 1 phần tử
e: E=N
=>Có vô số phần tử