
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: (x-4)(x+5)>0
=>x-4>0 hoặc x+5<0
=>x>4 hoặc x<-5
b: (2x+1)(x-3)<0
=>2x+1>0 và x-3<0
=>-1/2<x<3
c: (x-7)(3-x)<0
=>(x-7)(x-3)>0
=>x>7 hoặc x<3
d: x^2+6x-16<0
=>(x+8)(x-2)<0
=>-8<x<2
e: 3x^2+7x+4<0
=>3x^2+3x+4x+4<0
=>(x+1)(3x+4)<0
=>3x+4>0 và x+1<0
=>-4/3<x<-1
f: 5x^2-9x+4>0
=>(x-1)(5x-4)>0
=>x>1 hoặc x<4/5
g: x^2+6x-16<0
=>(x+8)(x-2)<0
=>-8<x<2
h: x^2+4x-21>0
=>(x+7)(x-3)>0
=>x>3 hoặc x<-7
i: x^2-9x-22<0
=>(x-11)(x+2)<0
=>-2<x<11
l: 16x^2+40x+25<0
=>(2x+5)^2<0(loại)
m: 3x^2-4x-4>=0
=>3x^2-6x+2x-4>=0
=>(x-2)(3x+2)>=0
=>x>=2 hoặc x<=-2/3

\(7,\) \(a,\left(2x-3y\right)^2-\left(2x+3y\right)^2=\left(3x-2y\right)^2-\left(3x+2y\right)^2\)
\(\Leftrightarrow4x^2-12xy+9y^2-4x^2-12xy-9y^2=9x^2-12xy+4y^2-9x^2-12xy-4y^2\)
\(\Leftrightarrow-24xy=-24xy\) ( luôn đúng )
Vậy 2 đẳng thức ở 2 vế bằng nhau.
\(b,\left(a^2+b^2\right)\left(c^2+d^2\right)=\left(ac+bd\right)^2+\left(ad-bc\right)^2\)
\(\Leftrightarrow\left(ac\right)^2+\left(ad\right)^2+\left(bc\right)^2+\left(bd\right)^2=\left(ac\right)^2+2acbd+\left(bd\right)^2+\left(ad\right)^2-2adbc+\left(bc\right)^2\)
\(\Leftrightarrow\left(ac\right)^2+\left(ad\right)^2+\left(bc\right)^2+\left(bd\right)^2=\left(ac\right)^2+\left(ad\right)^2+\left(bc\right)^2+\left(bd\right)^2\) ( luôn đúng )
Vậy 2 đẳng thức ở 2 vế bằng nhau.
*Ở câu \(b,\) dòng thứ 3, vế phải triệt tiêu \(2acbd-2adbc\) \(=0\) nên mất rồi nha.

2:
a: BC=căn 15^2+20^2=25cm
AH=15*20/25=12cm
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
=>DE=AH=12cm
b: ΔAHB vuông tại H có HD vuông góc AB
nên AD*AB=AH^2
ΔAHC vuông tại H có HE vuông góc AC
nên AE*AC=AH^2
=>AD*AB=AE*AC
c: góc IAC+góc AED
=góc ICA+góc AHD
=góc ACB+góc ABC=90 độ
=>AI vuông góc ED
4:
a: góc BDH=góc BEH=góc DBE=90 độ
=>BDHE là hình chữ nhật
b: BDHE là hình chữ nhật
=>góc BED=góc BHD=góc A
Xét ΔBED và ΔBAC có
góc BED=góc A
góc EBD chung
=>ΔBED đồng dạng với ΔBAC
=>BE/BA=BD/BC
=>BE*BC=BA*BD
c: góc MBC+góc BED
=góc C+góc BHD
=góc C+góc A=90 độ
=>BM vuông góc ED


đặt biểu thức trên là A.ta có
Amin khi và chỉ khi \(3x^2\)min.....vì \(3x^2\)\(\ge1\)v x
Nên \(3x^2\)min = 1
\(3x^2-3x=1-3.x=-2x\)
vậy Amin=-2x

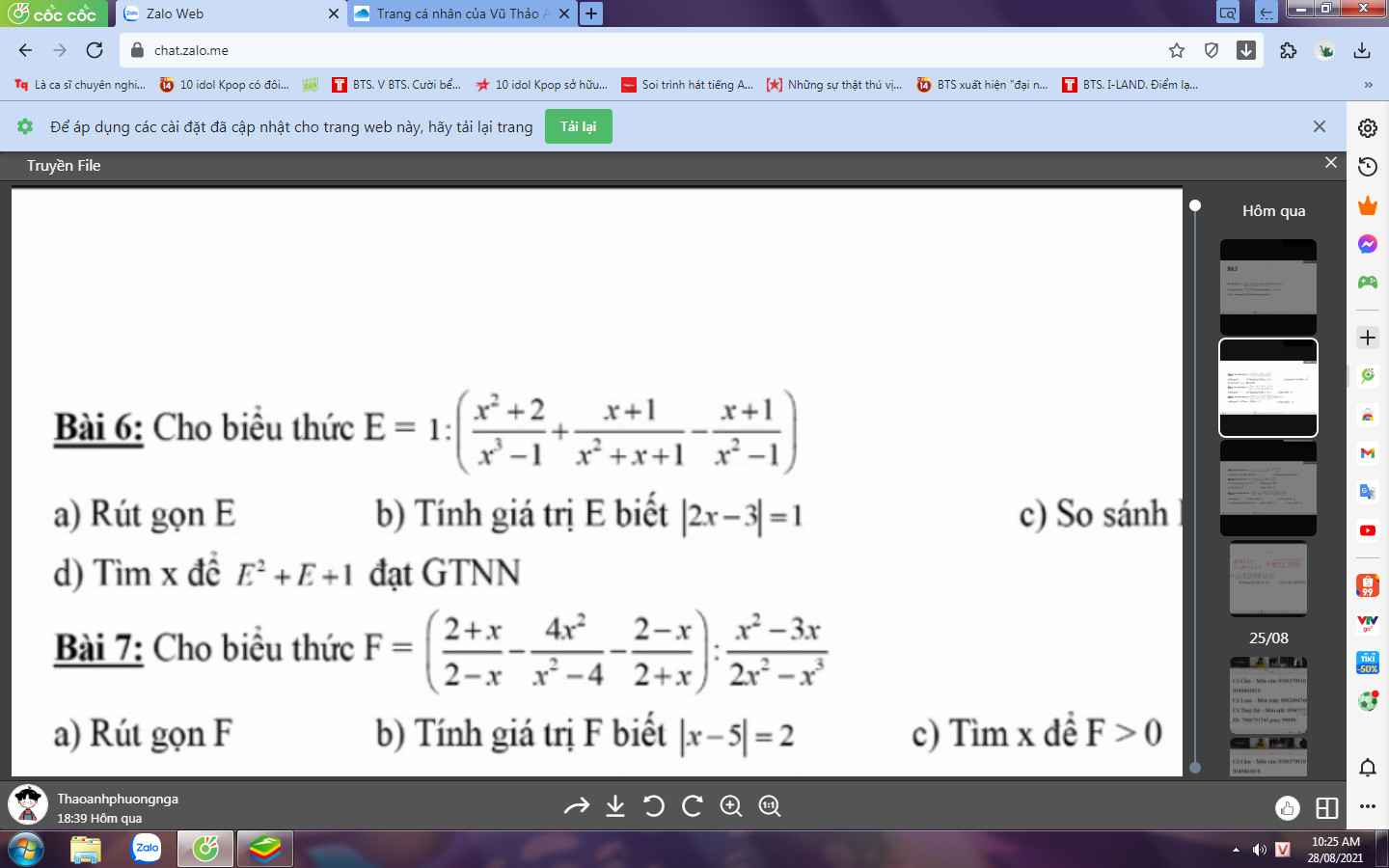
a. ĐKXĐ: \(x\ge4\)
\(F=\left(\dfrac{2+x}{2-x}-\dfrac{4x^2}{x^2-4}-\dfrac{2-x}{2+x}\right):\dfrac{x^2-3x}{2x^2-x^3}\)
\(=\left(\dfrac{\left(2+x\right)\left(2+x\right)}{\left(2-x\right)\left(2+x\right)}+\dfrac{4x^2}{\left(2-x\right)\left(2+x\right)}-\dfrac{\left(2-x\right)\left(2-x\right)}{\left(2-x\right)\left(2+x\right)}\right):\dfrac{x\left(x-3\right)}{x^2\left(2-x\right)}\)
\(=\dfrac{4+4x+x^2+4x^2-4+4x-x^2}{\left(2-x\right)\left(2+x\right)}.\dfrac{x^2\left(2-x\right)}{x\left(x-3\right)}\)
\(=\dfrac{4x^2+8x}{\left(2-x\right)\left(2+x\right)}.\dfrac{x^2\left(2-x\right)}{x\left(x-3\right)}=\dfrac{4x\left(x+2\right)x^2\left(2-x\right)}{\left(x+2\right)\left(2-x\right)x\left(x-3\right)}=\dfrac{4x^2}{x-3}\)
b. Ta có \(\left|x-5\right|=2\) \(\Leftrightarrow\left[{}\begin{matrix}x-5=2\\5-x=2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=3\end{matrix}\right.\)
* Với \(x=7\), ta có biểu thức \(F=\dfrac{4.7^2}{7-3}=\dfrac{196}{4}=49\)
* Với \(x=3\), ta có biểu thức \(F=\dfrac{4.3^2}{3-3}=\dfrac{36}{0}\), lúc này biểu thức không xác định
c. \(F>0\Leftrightarrow\dfrac{4x^2}{x-3}>0\), vì \(4x^2\ge0\forall x\) nên để \(\dfrac{4x^2}{x-3}>0\) thì \(\left\{{}\begin{matrix}4x^2>0\\x-3>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x>0\\x>3\end{matrix}\right.\) \(\Leftrightarrow x>3\)
\(4x^2>0\) thì không tương đương với \(x>0\) mà tương đương với \(x\ne0\)
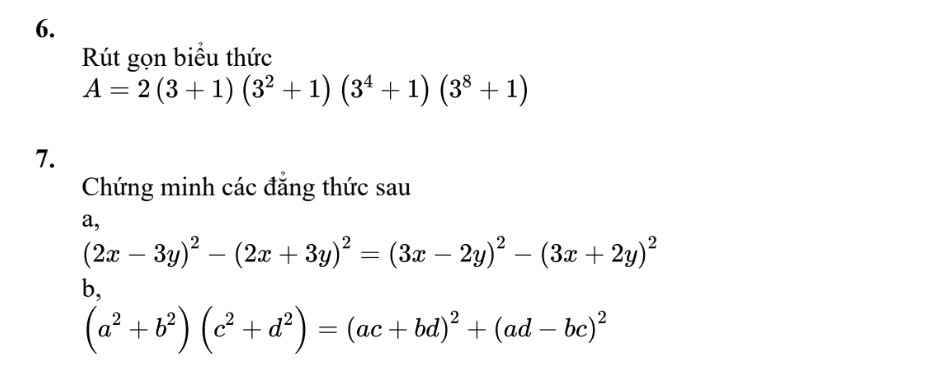
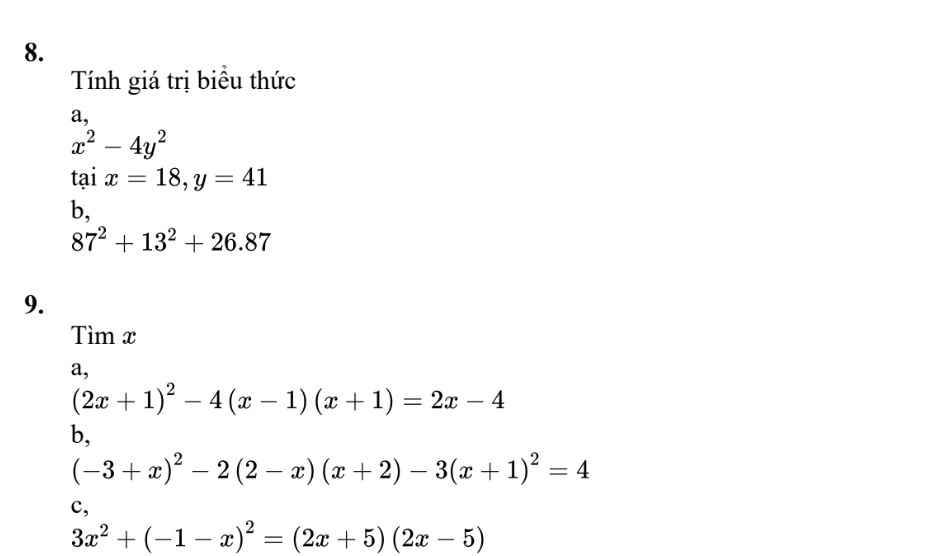








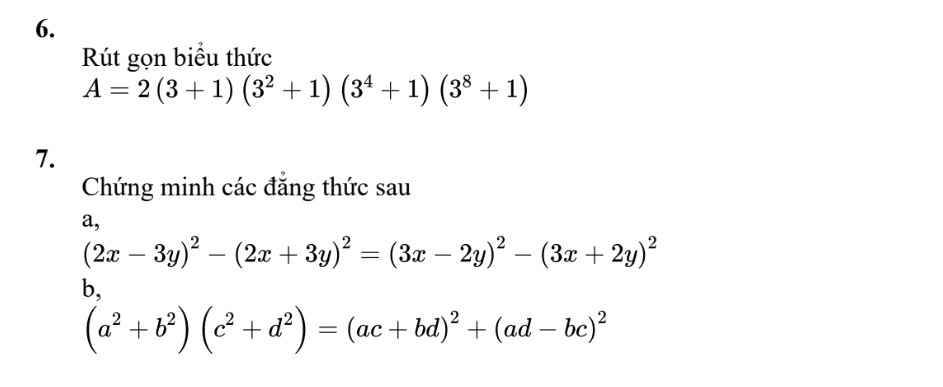
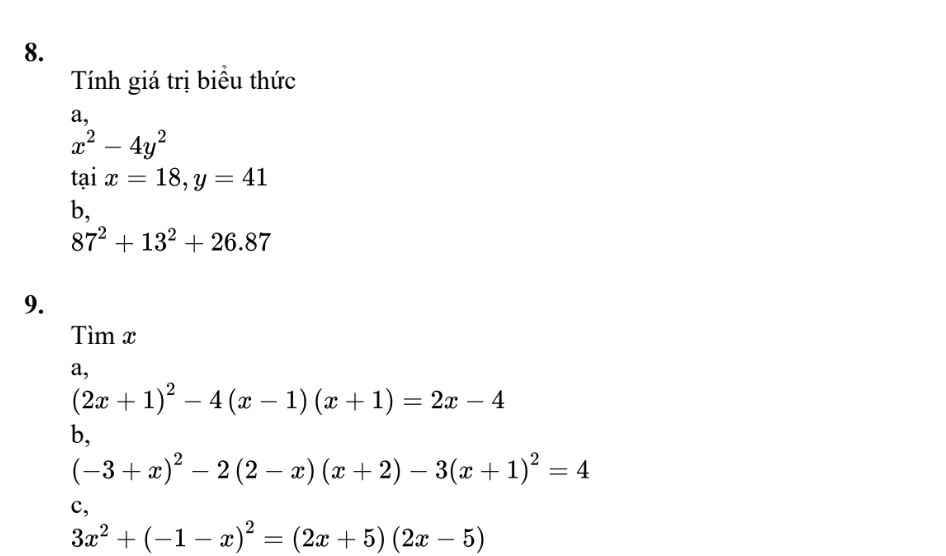

`@` `\text {Ans}`
`\downarrow`
`8,`
`a,`
Thay \(x=18;y=41\) vào bt
\(18^2-4\cdot41^2\)
`= 18^2 - (2*41)^2`
`= 18^2 - 82^2`
`= -6400`
`b,`
\(87^2+13^2+26\cdot87\)
`= 87*(87+26) + 169`
`= 87*113 + 169`
`= 9831 + 169`
`= 10000`
\(9,\) \(a,\left(2x+1\right)^2-4\left(x-1\right)\left(x+1\right)=2x-4\)
\(\Leftrightarrow4x^2+4x+1-4\left(x^2-1\right)-2x+4=0\)
\(\Leftrightarrow4x^2+4x+1-4x^2+4-2x+4=0\)
\(\Leftrightarrow\left(4x^2-4x^2\right)+\left(4x-2x\right)+\left(1+4+4\right)=0\)
\(\Leftrightarrow2x=-9\)
\(\Leftrightarrow x=-\dfrac{9}{2}\)
Vậy \(S=\left\{-\dfrac{9}{2}\right\}\)
\(b,\left(-3+x\right)^2-2\left(2-x\right)\left(x+2\right)-3\left(x+1\right)^2=4\)
\(\Leftrightarrow9-6x+x^2-2\left(2x+4-x^2-2x\right)-3\left(x^2+2x+1\right)-4=0\)
\(\Leftrightarrow9-6x+x^2-4x-8+2x^2+4x-3x^2-6x-3-4=0\)
\(\Leftrightarrow-12x=6\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy \(S=\left\{-\dfrac{1}{2}\right\}\)
\(c,3x^2+\left(-1-x\right)^2=\left(2x+5\right)\left(2x-5\right)\)
\(\Leftrightarrow3x^2+1+2x+x^2=4x^2-25\)
\(\Leftrightarrow2x=-26\)
\(\Leftrightarrow x=-13\)
Vậy \(S=\left\{-13\right\}\)