NT
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PL
1
29 tháng 6 2023
a: Xét ΔEAD và ΔECG có
góc EAD=góc ECG
góc AED=góc CEG
=>ΔEAD đồng dạng với ΔECG
=>AD/CG=ED/EG
=>AD*EG=ED*CG
b: Xét ΔHEG và ΔHCB có
góc HEG=góc HCB
góc EHG=góc CHB
=>ΔHEG đồng dạng với ΔHCB
=>HE/HC=HG/HB
Xét ΔHAB và ΔHCG có
góc HAB=góc HCG
góc AHB=góc CHG
=>ΔHAB đồng dạng với ΔHCG
=>HA/HC=HB/HG
=>HC/HA=HG/HB
=>HC/HA=HE/HC
=>HC^2=HA*HE
c: HI//BA
=>HI/BA=CH/CA=CI/CB
HI//EG
=>HI/EG=BI/BC
HI/BA=CI/CB
HI/BA+HI/EG=BI/BC+CI/BC=1
=>HI(1/BA+1/EG)=1
=>1/BA+1/EG=1/HI
24 tháng 12 2021
a: \(A=\dfrac{2x^2+x^2-1-2x^2+2x+1}{x\left(x+1\right)}=\dfrac{x^2+2x}{x\left(x+1\right)}=\dfrac{x+2}{x+1}\)
29 tháng 6 2023
a: Xét ΔEAD và ΔECG có
góc EAD=góc ECG
góc AED=góc CEG
=>ΔEAD đồng dạng với ΔECG
=>AD/CG=ED/EG
=>AD*EG=ED*CG
b: Xét ΔHEG và ΔHCB có
góc HEG=góc HCB
góc EHG=góc CHB
=>ΔHEG đồng dạng với ΔHCB
=>HE/HC=HG/HB
Xét ΔHAB và ΔHCG có
góc HAB=góc HCG
góc AHB=góc CHG
=>ΔHAB đồng dạng với ΔHCG
=>HA/HC=HB/HG
=>HC/HA=HG/HB
=>HC/HA=HE/HC
=>HC^2=HA*HE
c: HI//BA
=>HI/BA=CH/CA=CI/CB
HI//EG
=>HI/EG=BI/BC
HI/BA=CI/CB
HI/BA+HI/EG=BI/BC+CI/BC=1
=>HI(1/BA+1/EG)=1
=>1/BA+1/EG=1/HI
TK
2
9 tháng 12 2021
\(a,=\dfrac{4xy-1-2xy+1}{5x^2y}=\dfrac{6xy}{5x^2y}=\dfrac{6}{5x}\\ b,=\dfrac{x^2+8x-2x+8}{x\left(x-4\right)\left(x+4\right)}=\dfrac{\left(x+2\right)\left(x+4\right)}{x\left(x-4\right)\left(x+4\right)}=\dfrac{x+2}{x\left(x-4\right)}\\ c,=\dfrac{x^2+3x-x+1}{x\left(x+1\right)\left(x-1\right)}=\dfrac{\left(x+1\right)^2}{x\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{x\left(x-1\right)}\\ d,=\dfrac{x-3-x-3-2x}{\left(x-3\right)\left(x+3\right)}=\dfrac{-2\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{3-x}\\ e,=\dfrac{x+1-1}{x+1}=\dfrac{x}{x+1}\\ f,=\dfrac{3x+5-5+9x}{6x^2y}=\dfrac{12x}{6xy}=\dfrac{2}{y}\)
9 tháng 12 2021
\(g,=\dfrac{x^2+6x-2x+4}{x\left(x+2\right)\left(x-2\right)}=\dfrac{\left(x+2\right)^2}{x\left(x+2\right)\left(x-2\right)}=\dfrac{x+2}{x\left(x-2\right)}\\ h,=\dfrac{3x+1-3x+1+2x-3}{\left(3x-1\right)\left(3x+1\right)}=\dfrac{2x-1}{\left(3x-1\right)\left(3x+1\right)}\\ j,=\dfrac{5x+30+x^2-30}{x\left(x+6\right)}=\dfrac{x^2+5x}{x^2+6x}\\ k,=\dfrac{\left(x-7\right)\left(x+7\right)}{2x+1}\cdot\dfrac{-3}{x-7}=\dfrac{-3\left(x+7\right)}{2x+1}\\ l,=\dfrac{x\left(3x-2\right)}{x^2-1}\cdot\dfrac{\left(x^2+1\right)\left(x^2-1\right)}{\left(3x-2\right)^3}=\dfrac{x\left(x^2+1\right)}{\left(3x-2\right)^2}\)
27 tháng 12 2021
\(1,\\ a,=3x^2y-2xy^2-2xy^2=3x^2y-4xy^2\\ b,=\left(x+2\right)^2:\left(x+2\right)=x+2\\ c,=\dfrac{2}{x}\\ 2,\\ 1,\\ a,=2\left(x^2-2x+1\right)=2\left(x-1\right)^2\\ b,=\left(x-y\right)\left(x+y\right)+3\left(x-y\right)=\left(x-y\right)\left(x+y+3\right)\\ 2,\\ a,\Leftrightarrow x\left(x+5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\\ b,\Leftrightarrow3x\left(x-1\right)+\left(x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(3x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\\ 3,\\ a,ĐK:x\ne\pm1\\ b,A=\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{x-1}\\ c,A=2\Leftrightarrow\dfrac{x+1}{x-1}=2\Leftrightarrow x+1=2x-2\Leftrightarrow x=3\left(tm\right)\)
17 tháng 8 2021
\(a)\)
\(\frac{1}{x+1}-\frac{x-1}{x}=\frac{3x+1}{x\left(x+1\right)}\)
\(\Leftrightarrow x-x^2+1=3x+1\)
\(\Leftrightarrow x^2-2x=0\)
\(\Leftrightarrow x\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=2\end{cases}}\)
\(b)\)
\(\frac{\left(x+2\right)^2}{2x-3}-\frac{1}{1}=\frac{x^2+10}{2x-3}\)
\(\Leftrightarrow x^2+4x+4-2x-3=x^2+10\)
\(\Leftrightarrow x^2+2x+1=x^2+10\)
\(\Leftrightarrow2x-9=0\)
\(\Leftrightarrow2x=9\)
\(\Leftrightarrow x=\frac{2}{9}\)
20 tháng 9 2021
a: Xét ΔADM và ΔCBN có
AD=CB
\(\widehat{DAM}=\widehat{BCN}\)
AM=CN
Do đó: ΔADM=ΔCBN
Suy ra: DM=BN
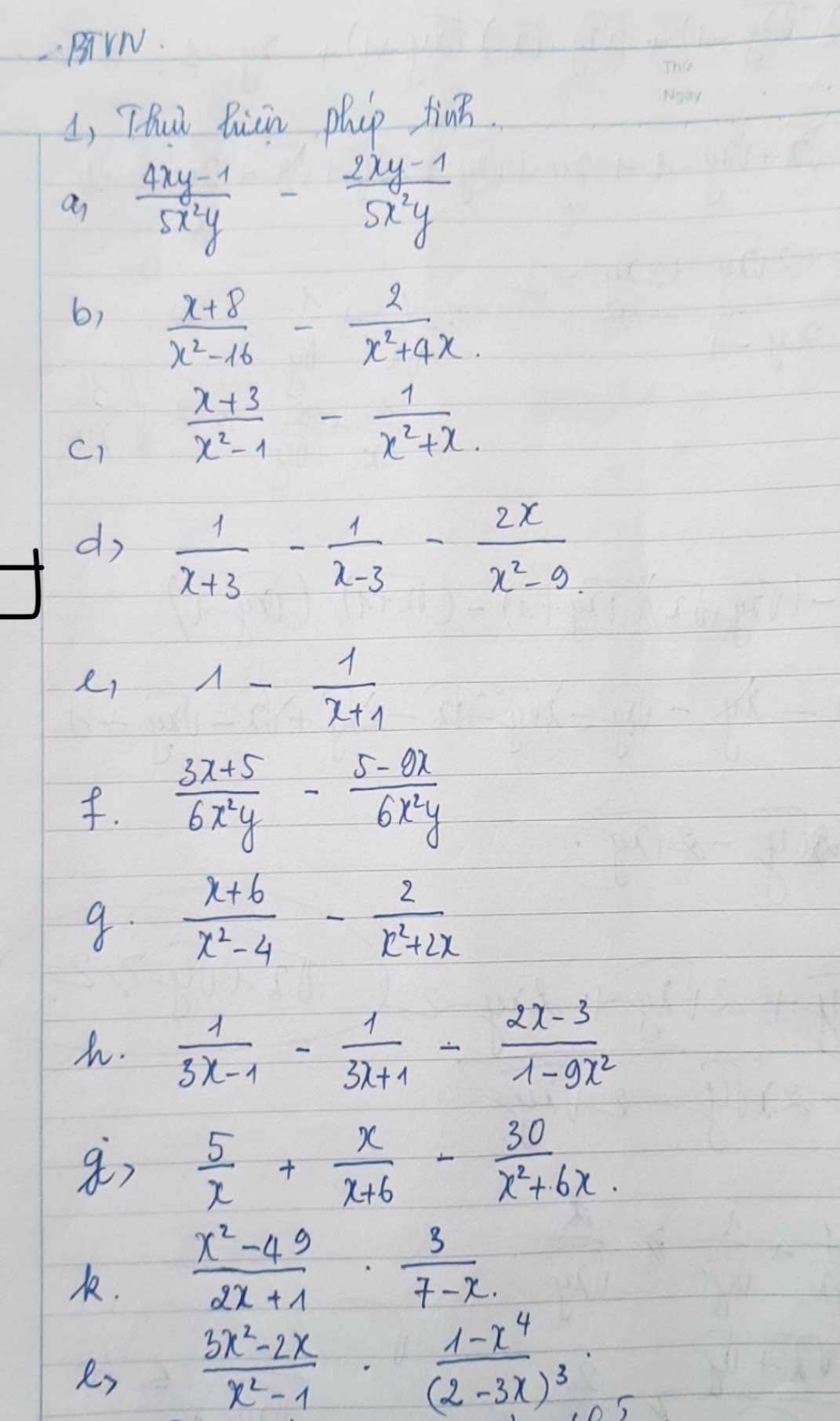
\(a.=x\)
\(b.=y^3\)
\(c.=3xy\)
\(d.=-\frac{5}{2}a\)
\(e.=3yz\)
\(f.=-3xy\)
làm cả bước giải ra đc ko ạ?