
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: A=-1/2*xy^3*4x^2y^2=-2x^3y^5
Bậc là 8
Phần biến là x^3;y^5
Hệ số là -2
2:
a: P(x)=3x+4x^4-2x^3+4x^2-x^4-6
=3x^4-2x^3+4x^2+3x-6
Q(x)=2x^4+4x^2-2x^3+x^4+3
=3x^4-2x^3+4x^2+3
b: A(x)=P(x)-Q(x)
=3x^4-2x^3+4x^2+3x-6-3x^4+2x^3-4x^2-3
=3x-9
A(x)=0
=>3x-9=0
=>x=3


có: tam giác ABO cân tại A (gt)
=> AB=AO (tính chất tam giác cân)
Có: AH vuông góc BO (gt)
=> góc AHB = góc AHO (tính chất đường vuông góc)
Xét tam giác AHB và tam giác AHO có
goc AHB = góc AHO (cmt)
AB = AO (cmt)
AH chung
=> tam giác AHB = tam giác AHO (cạnh huyền - cạnh góc vuông)

Gọi độ dài 3 cạnh tam giác lần lượt là a,b,c
Điều kiện: a,b,c >0
Vì tam giác có chu vi bằng 45cm
⇒ a+b+c=45
Vì độ dài 3 cạnh lần lượt tỉ lệ với 4;5;6
⇒ \(\dfrac{a}{4}=\dfrac{b}{5}=\dfrac{c}{6}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{a}{4}=\dfrac{b}{5}=\dfrac{c}{6}=\dfrac{a+b+c}{4+5+6}=\dfrac{45}{15}=3\)
⇒\(\left\{{}\begin{matrix}a=3.4=12\\b=3.5=15\\c=3.6=18\end{matrix}\right.\)
Vậy .....


Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó:MN là đường trung bình
=>MN//BC và MN=BC/2
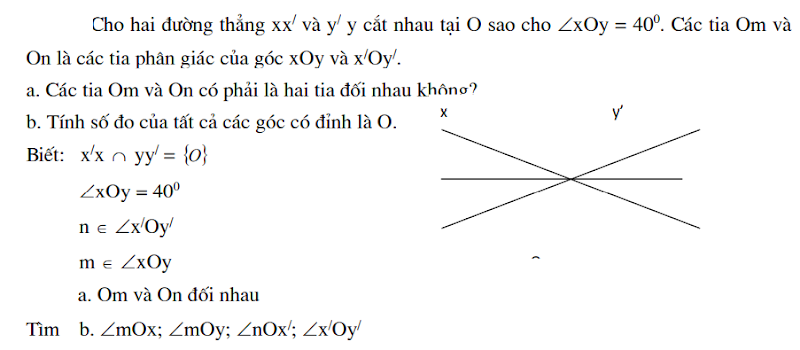 giúp mình vs nha cảm ơn mn nhìu
giúp mình vs nha cảm ơn mn nhìu

 giúp mình với, mk cần gấp ạ, cảm ơn mn rất nhìu !
giúp mình với, mk cần gấp ạ, cảm ơn mn rất nhìu !