K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 10 2021
\(a,A=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ A=\dfrac{2x-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(2\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\\ b,A=\dfrac{2\left(\sqrt{x}+1\right)-3}{\sqrt{x}+1}=2-\dfrac{3}{\sqrt{x}+1}\in Z\\ \Leftrightarrow\sqrt{x}+1\inƯ\left(3\right)=\left\{1;3\right\}\left(\sqrt{x}+1\ge1\right)\\ \Leftrightarrow\sqrt{x}\in\left\{0;2\right\}\\ \Leftrightarrow x\in\left\{0;4\right\}\left(tm\right)\)
25 tháng 10 2021
a) \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{3\sqrt{x}+1}{x-1}\)
\(\Rightarrow A=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{2x-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{\left(2x-2\sqrt{x}\right)-\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{2\sqrt{x}\left(\sqrt{x}-1\right)-\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{\left(2\sqrt{x}-1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)
31 tháng 7 2023
1:
a: \(P=B:A\)
\(=\dfrac{3\sqrt{x}-3-2\sqrt{x}+4+\sqrt{x}+2}{x-4}:\dfrac{4\sqrt{x}-1}{x-4}\)
\(=\dfrac{2\sqrt{x}+3}{x-4}\cdot\dfrac{x-4}{4\sqrt{x}-1}=\dfrac{2\sqrt{x}+3}{4\sqrt{x}-1}\)
b: Để P nguyên thì \(2\sqrt{x}+3⋮4\sqrt{x}-1\)
=>\(4\sqrt{x}+6⋮4\sqrt{x}-1\)
=>\(4\sqrt{x}-1+7⋮4\sqrt{x}-1\)
=>4căn x-1 thuộc {1;-1;7;-7}
=>căn x thuộc {1/2;0;2}
mà x nguyên và x>=0 và x<>4
nên x thuộc {0}
Y
11 tháng 7 2023
\(a,A=\sqrt{\left(2-\sqrt{5}\right)^2}+\sqrt{\left(2\sqrt{2}-\sqrt{5}\right)^2}\\ =\left|2-\sqrt{5}\right|+\left|2\sqrt{2}-\sqrt{5}\right|\\ =\sqrt{5}-2+2\sqrt{2}-5\\ =2\sqrt{2}-2\)
\(b,B=\sqrt{\left(\sqrt{7}-2\sqrt{2}\right)^2}+\sqrt{\left(3-2\sqrt{2}\right)^2}\\ =\left|\sqrt{7}-2\sqrt{2}\right|+\left|3-2\sqrt{2}\right|\\ =2\sqrt{2}-\sqrt{7}+3-2\sqrt{2}\\ =-\sqrt{7}+3\)
NH
11 tháng 7 2023
a)
\(A=\sqrt{\left(2-\sqrt{5}\right)^2}+\sqrt{\left(2\sqrt{2}-\sqrt{5}\right)^2}\\ =\left|2-\sqrt{5}\right|+\left|2\sqrt{2}-\sqrt{5}\right|\)
\(=\sqrt{5}-2+2\sqrt{2}-\sqrt{5}\) (vì \(2-\sqrt{5}< 0;2\sqrt{2}-\sqrt{5}>0\) )
\(=2\sqrt{2}-2\)
b)
\(B=\sqrt{\left(\sqrt{7}-2\sqrt{2}\right)^2}+\sqrt{\left(3-2\sqrt{2}\right)^2}\\ =\left|\sqrt{7}-2\sqrt{2}\right|+\left|3-2\sqrt{2}\right|\)
\(=2\sqrt{2}-\sqrt{7}+3-2\sqrt{2}\) (vì \(\sqrt{7}-2\sqrt{2}< 0;3-2\sqrt{2}>0\) )
\(=3-\sqrt{7}\)
29 tháng 8 2023
\(P=\dfrac{Q}{R}=\dfrac{3\sqrt{x}-1}{x-4}:\dfrac{2}{\sqrt{x}-2}\)
\(=\dfrac{3\sqrt{x}-1}{x-4}\cdot\dfrac{\sqrt{x}-2}{2}=\dfrac{3\sqrt{x}-1}{2\sqrt{x}+4}\)
P là số nguyên
=>\(3\sqrt{x}-1⋮2\sqrt{x}+4\)
=>\(6\sqrt{x}-2⋮2\sqrt{x}+4\)
=>\(6\sqrt{x}+12-14⋮2\sqrt{x}+4\)
=>\(2\sqrt{x}+4\inƯ\left(-14\right)\)
mà 2*căn x+4>=4
nên \(2\sqrt{x}+4\in\left\{7;14\right\}\)
=>\(2\sqrt{x}\in\left\{3;10\right\}\)
=>\(x\in\left\{\dfrac{9}{4};25\right\}\)
H9
HT.Phong (9A5)
CTVHS
30 tháng 8 2023
Ta có:
\(\dfrac{Q}{R}\) là:
\(\dfrac{3\sqrt{x}-1}{x-4}:\dfrac{2}{\sqrt{x}-2}\) (ĐK: \(x\ge0;x\ne4\))
\(=\dfrac{3\sqrt{x}-1}{\left(\sqrt{x}\right)^2-2^2}:\dfrac{2}{\sqrt{x}-2}\)
\(=\dfrac{3\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{\left(3\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{2\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\sqrt{x}-1}{2\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\sqrt{x}-1}{2\sqrt{x}+4}\)
Để giá trị của biểu thức \(\dfrac{Q}{R}\) nguyên thì
\(3\sqrt{x}-1\) chia hết cho \(2\sqrt{x}+4\)
⇒ \(2\left(3\sqrt{x}-1\right)\) chia hết cho \(2\sqrt{x}+4\)
⇒ \(6\sqrt{x}-2\) chia hết cho \(2\sqrt{x}+4\)
⇒ \(6\sqrt{x}+12-14\) chia hết cho \(2\sqrt{x}+4\)
⇒ \(3\left(2\sqrt{x}+4\right)-14\) chia hết cho \(2\sqrt{x}+4\)
⇒ - 14 chia hết cho \(2\sqrt{x}+4\)
Mà: Ư(-14)\(=\left\{1;-1;2;-2;7;-7;14;-14\right\}\)
ĐK: \(2\sqrt{x}+4\ge4\)
\(\Rightarrow2\sqrt{x}+4\in\left\{7;14\right\}\)
\(\Rightarrow x\in\left\{\dfrac{9}{4};25\right\}\)
17 tháng 10 2021
Bài 8:
a: Thay x=16 vào P, ta được:
\(P=\dfrac{4+2}{4-1}=\dfrac{6}{3}=2\)
b: Thay \(x=3+2\sqrt{2}\) vào P, ta được:
\(P=\dfrac{\sqrt{2}+1+2}{\sqrt{2}+1-1}=\dfrac{3+\sqrt{2}}{\sqrt{2}}=3\sqrt{2}+2\)
20 tháng 8 2021
Lần sau đăng tách bài ra bạn nhé.
Câu 8
Câu 1, ý a và b:
20 tháng 8 2021
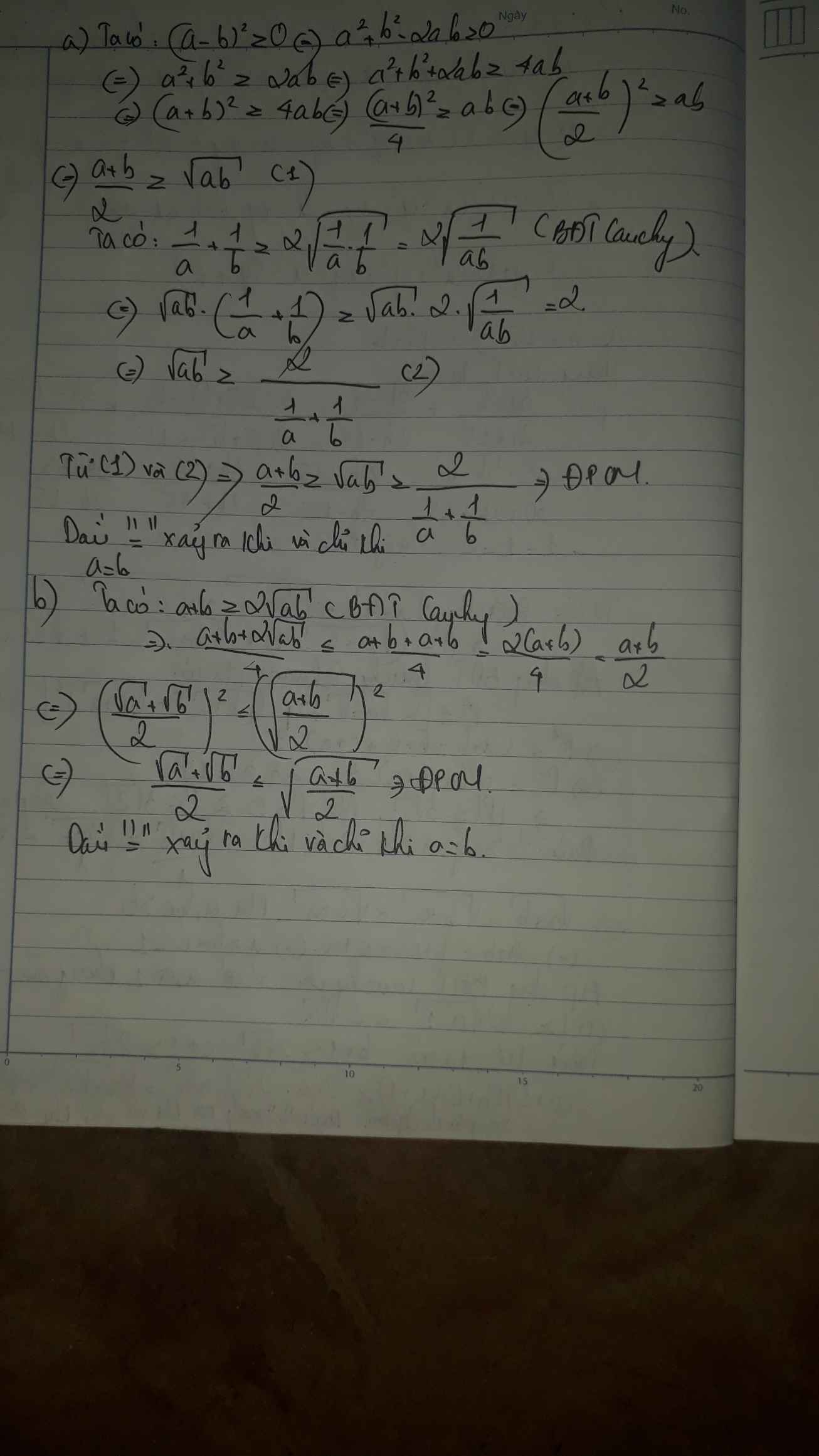
Câu 7:
Ta có: \(\dfrac{x}{\sqrt{4x-1}}\ge\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{2x-\sqrt{4x-1}}{2\sqrt{4x-1}}\ge0\)
\(\Leftrightarrow2x-\sqrt{4x-1}\ge0\)
\(\Leftrightarrow4x-2\sqrt{4x-1}\ge0\)
\(\Leftrightarrow4x-1-2\cdot\sqrt{4x-1}\cdot1+1\ge0\)
\(\Leftrightarrow\left(\sqrt{4x-1}-1\right)^2\ge0\forall x\) thỏa mãn ĐKXĐ
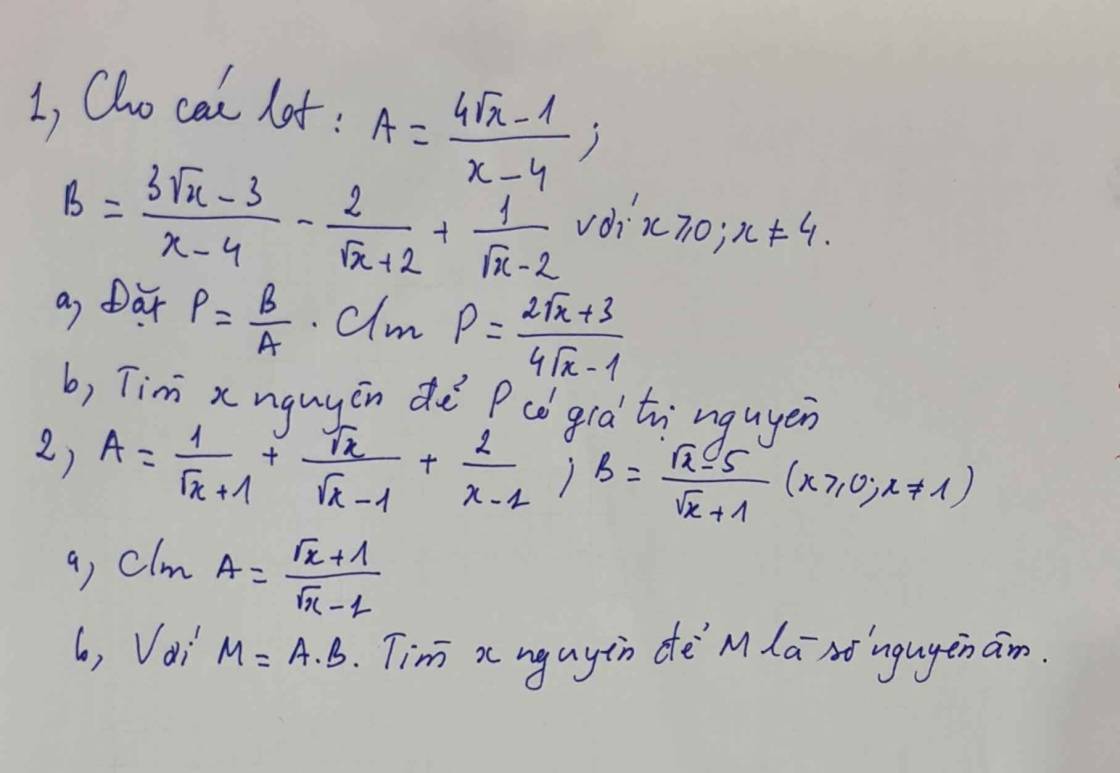
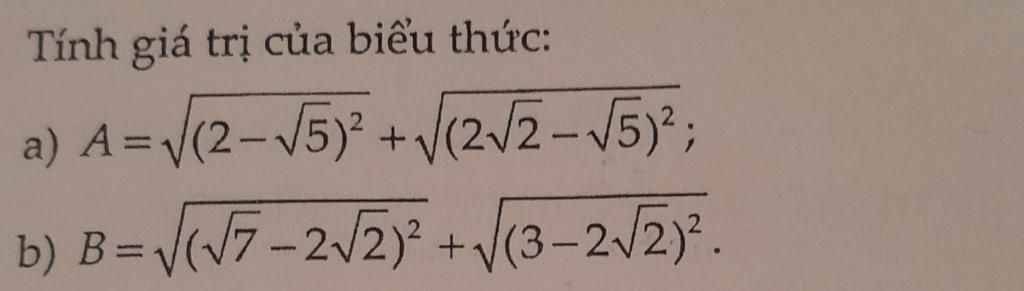
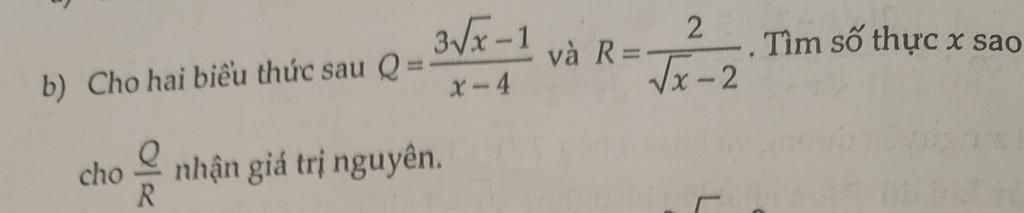
Xét (O) có
AB là tiếp tuyến có B là tiếp điểm
AC là tiếp tuyến có C là tiếp điểm
Do đó: AB=AC
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(1)
Ta có: AB=AC
nên A nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
hay OA\(\perp\)BC