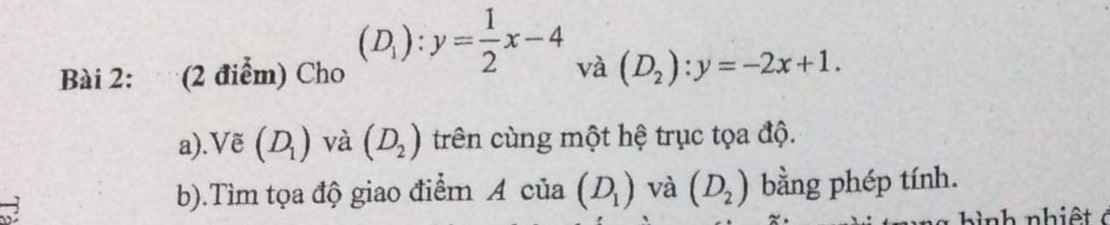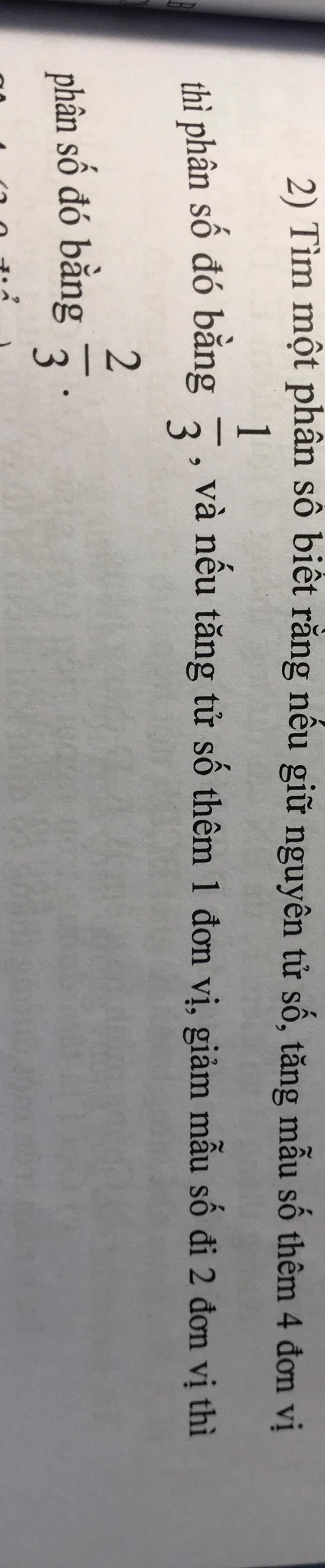K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 10 2021
Bài 8:
a: Thay x=16 vào P, ta được:
\(P=\dfrac{4+2}{4-1}=\dfrac{6}{3}=2\)
b: Thay \(x=3+2\sqrt{2}\) vào P, ta được:
\(P=\dfrac{\sqrt{2}+1+2}{\sqrt{2}+1-1}=\dfrac{3+\sqrt{2}}{\sqrt{2}}=3\sqrt{2}+2\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 1 2022
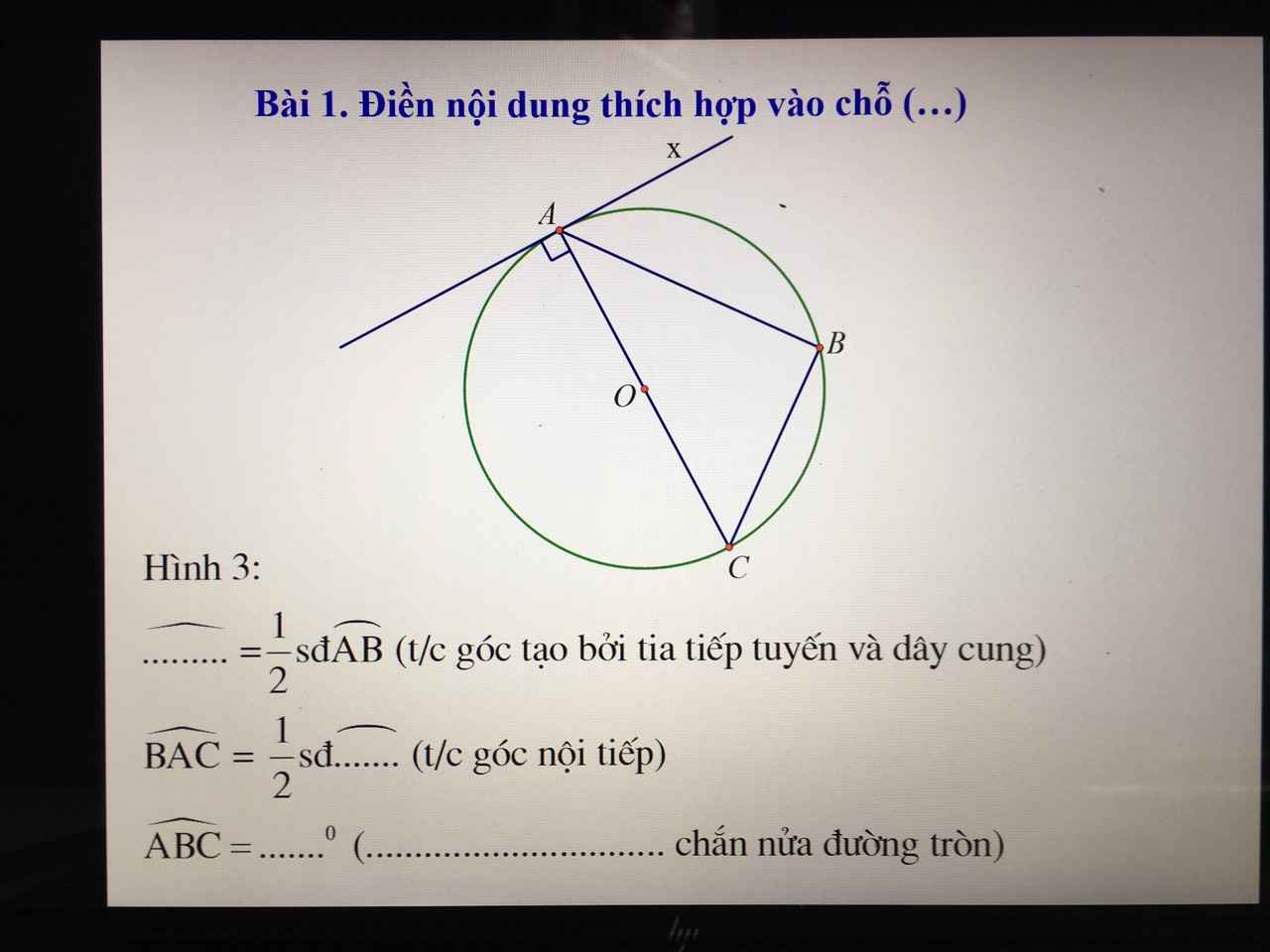
\(\widehat{BAx}=\dfrac{1}{2}sđ\stackrel\frown{AB}\)
\(\widehat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\)
\(\widehat{ABC}=90^0\) (góc nội tiếp chắn nửa đường tròn)
9 tháng 12 2023
Câu 2:
1: \(y=\sqrt{3}+5\)
=>\(\left(\sqrt{3}-1\right)x+4=\sqrt{3}+5\)
=>\(\left(\sqrt{3}-1\right)\cdot x=\sqrt{3}+5-4=\sqrt{3}+1\)
=>\(x=\dfrac{\sqrt{3}+1}{\sqrt{3}-1}=\dfrac{\left(\sqrt{3}+1\right)^2}{3-1}=\dfrac{4+2\sqrt{3}}{2}=2+\sqrt{3}\)
2: \(x^2-2\left(1-m\right)x-2m-5=0\)
=>\(x^2+\left(2m-2\right)x-2m-5=0\)
a: \(\Delta=\left(2m-2\right)^2-4\left(-2m-5\right)\)
\(=4m^2-8m+4+8m+20\)
\(=4m^2+24>=24>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
Câu 1:
2: Thay x=2 và y=-1 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}2a-\left(-1\right)=5\\b\cdot2+a\cdot\left(-1\right)=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a=5+\left(-1\right)=4\\2b-a=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\2b=a+4=6\end{matrix}\right.\)
=>a=2 và b=3
2: Gọi phân số cần tìm có dạng là \(\dfrac{a}{b}\left(b\ne0\right)\)
Khi tăng mẫu số thêm 4 đơn vị thì phân số đó bằng 1/3 nên ta có:
\(\dfrac{a}{b+4}=\dfrac{1}{3}\)
=>3a=b+4
=>3a-b=4(1)
Khi giảm mẫu số đi 2 đơn vị thì phân số bằng với 2/3 nên ta có:
\(\dfrac{a}{b-2}=\dfrac{2}{3}\)
=>3a=2(b-2)
=>3a=2b-4
=>3a-2b=-4(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a-b=4\\3a-2b=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=8\\3a-b=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=8\\3a=b+4=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=4\\b=8\end{matrix}\right.\)(nhận)
Vậy: Phân số cần tìm là \(\dfrac{4}{8}\)
20 tháng 8 2021
Lần sau đăng tách bài ra bạn nhé.
Câu 8
Câu 1, ý a và b:
20 tháng 8 2021
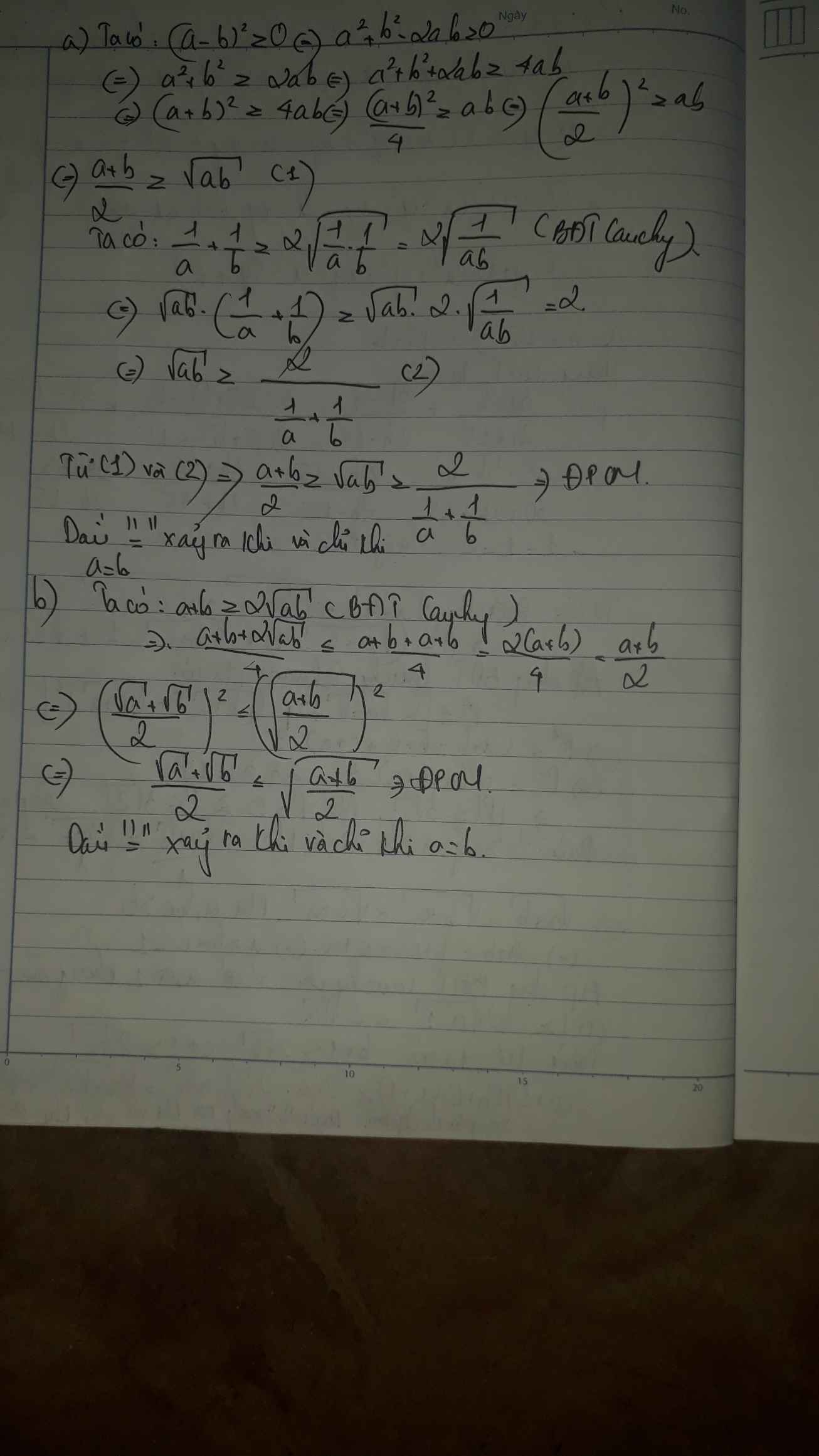
Câu 7:
Ta có: \(\dfrac{x}{\sqrt{4x-1}}\ge\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{2x-\sqrt{4x-1}}{2\sqrt{4x-1}}\ge0\)
\(\Leftrightarrow2x-\sqrt{4x-1}\ge0\)
\(\Leftrightarrow4x-2\sqrt{4x-1}\ge0\)
\(\Leftrightarrow4x-1-2\cdot\sqrt{4x-1}\cdot1+1\ge0\)
\(\Leftrightarrow\left(\sqrt{4x-1}-1\right)^2\ge0\forall x\) thỏa mãn ĐKXĐ
10 tháng 10 2021
f: Ta có: \(\sqrt{2-x}=\sqrt{x^2-2x+4}\)
\(\Leftrightarrow x^2-2x+4=2-x\)
\(\Leftrightarrow x^2-x+2=0\)
\(\Leftrightarrow x\in\varnothing\)