Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 11: D
Câu 12: D
Câu 13: C
Câu 14: B
Câu 15: C
Câu 16: C
Câu 18: C
Câu 17: A

a.
Lấy $x_1\neq x_2$ là $x_1,x_2\in (1;+\infty)$
Xét \(A=\frac{y(x_1)-y(x_2)}{x_1-x_2}\)
\(y(x_1)-y(x_2)=\frac{2x_1^2-x_1-3}{x_1-1}-\frac{2x_2^2-x_2-3}{x_2-1}=2(x_1-x_2)-(\frac{2}{x_1-1}-\frac{2}{x_2-1})\)
\(=2(x_1-x_2)+\frac{2(x_1-x_2)}{(x_1-1)(x_2-1)}=2(x_1-x_2)[1+\frac{1}{(x_1-1)(x_2-1)}]\)
\(\Rightarrow A=2[1+\frac{1}{(x_1-1)(x_2-1)}]>0\) với $x_1,x_2>1$
Vậy hàm số đồng biến trên TXĐ.
c.
Lấy $x_1\neq x_2\in [-3;+\infty)$
Xét $A=\frac{y(x_1)-y(x_2)}{x_1-x_2}$
\(=\frac{(\sqrt{x_1+5}-\sqrt{x_1+3})-(\sqrt{x_2+5}-\sqrt{x_2+3})}{x_1-x_2}\)
\(=\frac{(\sqrt{x_1+5}-\sqrt{x_2+5})-(\sqrt{x_1+3}-\sqrt{x_2+3})}{x_1-x_2}=\frac{1}{\sqrt{x_1+5}+\sqrt{x_2+5}}-\frac{1}{\sqrt{x_1+3}-\sqrt{x_2}+3}< 0\)
Do đó hàm nghịch biến trên TXĐ.
d. Lấy $x_1\neq x_2\in (-\infty; 0)$
Xét \(A=\frac{y(x_1)-y(x_2)}{x_1-x_2}=\frac{\sqrt{x_1^2+1}-\sqrt{x_2^2+1}}{x_1-x_2}=\frac{x_1^2-x_2^2}{(\sqrt{x_1^2+1}+\sqrt{x_2^2+1})(x_1-x_2)}\)
\(=\frac{x_1+x_2}{\sqrt{x_1^2+1}+\sqrt{x_2^2+1}}<0\) với mọi $x_1,x_2< 0$
Do đó hàm số nghịch biến trên $(-\infty; 0)$
e. Đặt $\sqrt{x+2}=t$ thì ta cần cm hàm:
$y=\frac{2t^2-5}{t}$ đồng biến trên $(0; \sqrt{2})$
Lấy $t_1\neq t_2\in (0;\sqrt{2})$
Xét \(A=\frac{y(t_1)-y(t_2)}{t_1-t_2}=\frac{2t_1-\frac{5}{t_1}-(2t_2-\frac{5}{t_2})}{t_1-t_2}=\frac{2(t_1-t_2)+\frac{5(t_1-t_2)}{t_1t_2}}{t_1-t_2}=2+\frac{5}{t_1t_2}>0\) với mọi $t\in (0;\sqrt{2})$
Vậy hàm số đồng biến.

Bài 9:
\(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}\)
\(=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{CB}\)
\(=\overrightarrow{0}\)

Mình thì biết giải khúc đầu rồi, nhưng mà chỗ +-2 ở đâu ra thì mình k biết :(( có lên gg coi nhưng k ai giải đáp hết


Hiểu như này:
\(\dfrac{a}{1+a}+\dfrac{b}{1+b}+\dfrac{b}{1+b}=3-\left(\dfrac{1}{1+a}+\dfrac{1}{1+b}+\dfrac{1}{1+b}\right)\le3-\dfrac{9}{1+a+1+b+1+b}=\dfrac{3\left(a+2b\right)}{3+a+2b}\)

18.
Do D thuộc trục hoành nên tọa độ có dạng: \(D\left(a;0;0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AD}=\left(a-3;4;0\right)\\\overrightarrow{BC}=\left(4;0;-3\right)\end{matrix}\right.\)
\(AD=BC\Leftrightarrow\left(a-3\right)^2+4^2=4^2+\left(-3\right)^2\)
\(\Rightarrow\left(a-3\right)^2=9\Rightarrow\left[{}\begin{matrix}a=0\\a=6\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}D\left(0;0;0\right)\\D\left(6;0;0\right)\end{matrix}\right.\)
19.
\(cos\left(\overrightarrow{a};\overrightarrow{b}\right)=\dfrac{2.\left(-1\right)+1.0+0.\left(-2\right)}{\sqrt{2^2+1^2+0^2}.\sqrt{\left(-1\right)^2+0^2+\left(-2\right)^2}}=-\dfrac{2}{5}\)
20.
\(\overrightarrow{OA}=\left(2;2;1\right)\Rightarrow OA=\sqrt{2^2+2^2+1^2}=3\)




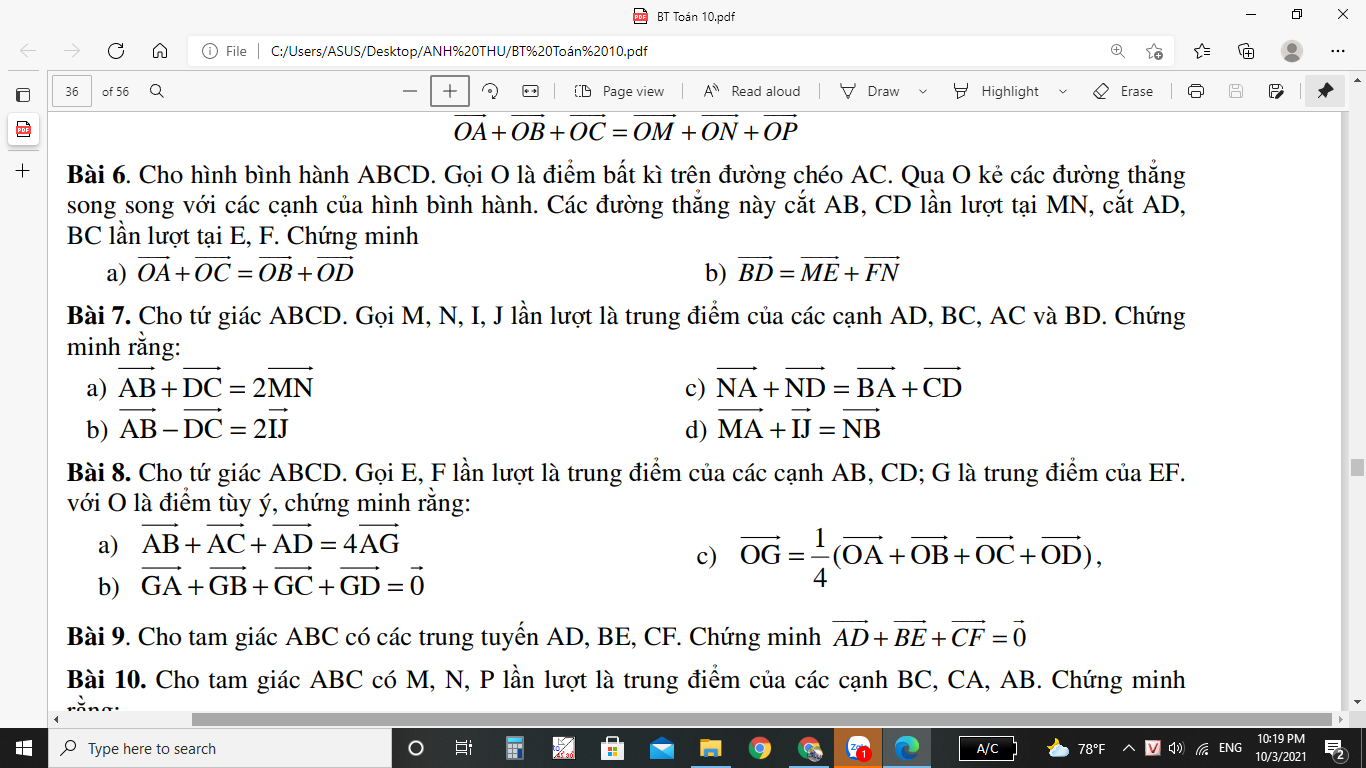 câu 8 làm thế nào vậy mn mình ko bt lm
câu 8 làm thế nào vậy mn mình ko bt lm



Câu 1: D
Câu 2: Những mệnh đề sai là: 2,3,4,5,7,8
=>Chọn B
Câu 3: C
Câu 4: A
Câu 5: D
Câu 6: D
Câu 7: D
Câu 8: C
Câu 9: D
Câu 10: B