K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NA
1
AH
Akai Haruma
Giáo viên
4 tháng 5 2023
Lời giải:
Gọi vận tốc ban đầu của người đi xe đạp là $a$ km/h.
Theo bài ra ta có:
$\frac{18}{a}+\frac{40-18}{a+2}=4$
$\Leftrightarrow \frac{18}{a}+\frac{22}{a+2}=4$
$\Leftrightarrow \frac{18(a+2)+22a}{a(a+2)}=4$
$\Leftrightarrow \frac{40a+36}{a^2+2a}=4$
$\Rightarrow 40a+36=4a^2+8a$
$\Leftrightarrow 4a^2-32a-36=0$
$\Leftrightarrow a^2-8a-9=0$
$\Leftrightarrow (a+1)(a-9)=0$
Vì $a>0$ nên $a=9$ (km.h)
LB
1
25 tháng 8 2021
Câu 3:
2: Xét tứ giác OKEH có
\(\widehat{OKE}=\widehat{OHE}=\widehat{KOH}=90^0\)
Do đó: OKEH là hình chữ nhật
mà đường chéo OE là tia phân giác của \(\widehat{KOH}\)
nên OKEH là hình vuông
26 tháng 6 2021
a) Thay x=4(TMĐK) vào B ta có:
\(B=\dfrac{4-\sqrt{4}}{2\sqrt{4}+1}=\dfrac{2}{5}\)
Vậy x=4 thì B=\(\dfrac{2}{5}\)
b)\(M=A.B\)
M =\(\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right).\dfrac{x-\sqrt{x}}{2\sqrt{x}+1}\)
M= \(\left(\dfrac{1}{\sqrt{x-1}}+\dfrac{\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right).\dfrac{x-\sqrt{x}}{2\sqrt{x}+1}\)
M= \(\dfrac{2\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{2\sqrt{x}+1}\)
M= \(\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
c)\(M=\dfrac{1}{3}\)
\(\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}+1}=\dfrac{1}{3}\)
\(\Leftrightarrow3\sqrt{x}=\sqrt{x}+1\)
\(\Leftrightarrow2\sqrt{x}=1\)
\(\Leftrightarrow\sqrt{x}=\dfrac{1}{2}\)
\(\Leftrightarrow x=\dfrac{1}{4}\)
Vậy với x=\(\dfrac{1}{4}\) thì M=\(\dfrac{1}{3}\)
26 tháng 6 2021
`a)x=64`
`=>N=sqrtx/(sqrtx-3)=8/(8-3)=8/5`
`b)M=(2sqrtx)/(sqrtx-3)-(x+9sqrtx)/(x-9)`
`=(2x+6sqrtx-x-9sqrtx)/(x-9)`
`=(x-3sqrtx)/(x-9)`
`=sqrtx/(sqrtx+3)`
`P=M.N=x/(x-9)`
`c)` So sánh gì với 1?
26 tháng 6 2021
a) Thay x=64(TMĐK) vào N ta có:
\(N=\dfrac{\sqrt{64}}{\sqrt{64}-5}=\dfrac{8}{3}\)
Vậy x=64 thì N=\(\dfrac{8}{3}\)
b) \(P=M.N\)
\(P=\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{x-9\sqrt{x}}{x-9}.\left(\dfrac{\sqrt{x}}{\sqrt{x}-5}\right)\)
\(P=\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{x-9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\left(\dfrac{\sqrt{x}}{\sqrt{x}-5}\right)\)
\(P=\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)-x+9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\dfrac{\sqrt{x}}{\sqrt{x}+5}\)
\(P=\dfrac{x+15\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\dfrac{\sqrt{x}}{\sqrt{x}+5}\)
\(P=\dfrac{x}{\left(\sqrt{x}-3\right)\left(\sqrt{x} +3\right)}\)
\(P=\dfrac{x}{x-9}\)
4 tháng 5 2021
Bài 1: Em chuyển vế đưa về y=3-3x ví dụ vậy và thế vào phương trình dưới giải ra
câu b thì em đưa ra x=(11+2y)/3 xong thế vào pt dưới giải luôn
câu c thì em cho y=4-2x rồi em thế vào pt trên rồi giải ra
N
23 tháng 11 2021
\(1,A=10\sqrt{2}+5\sqrt{2}-6\sqrt{2}=9\sqrt{2}\\ B=6\sqrt{3}-4\sqrt{3}-\sqrt{3}=\sqrt{3}\\ 2,\\ a,ĐK:1-3x\ge0\Leftrightarrow x\le\dfrac{1}{3}\\ b,ĐK:x\ge0;x\ne4\\ 3,\\ a,\Leftrightarrow12x-3=4\Leftrightarrow x=\dfrac{7}{12}\\ b,\Leftrightarrow\left|2x-1\right|=5\Leftrightarrow\left[{}\begin{matrix}2x-1=5\\1-2x=5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\\ c,\Leftrightarrow\left|3x-1\right|=5\Leftrightarrow\left[{}\begin{matrix}3x-1=5\\1-3x=5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{4}{3}\end{matrix}\right.\)
\(4,\\ B=\dfrac{a+2\sqrt{a}+1+a-2\sqrt{a}+1}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{4\left(a+1\right)}\\ B=\dfrac{2\left(a+1\right)}{4\left(a+1\right)}=\dfrac{1}{2}\)
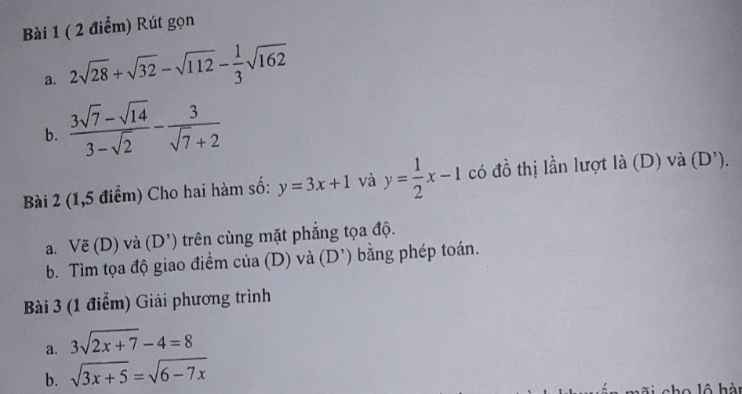
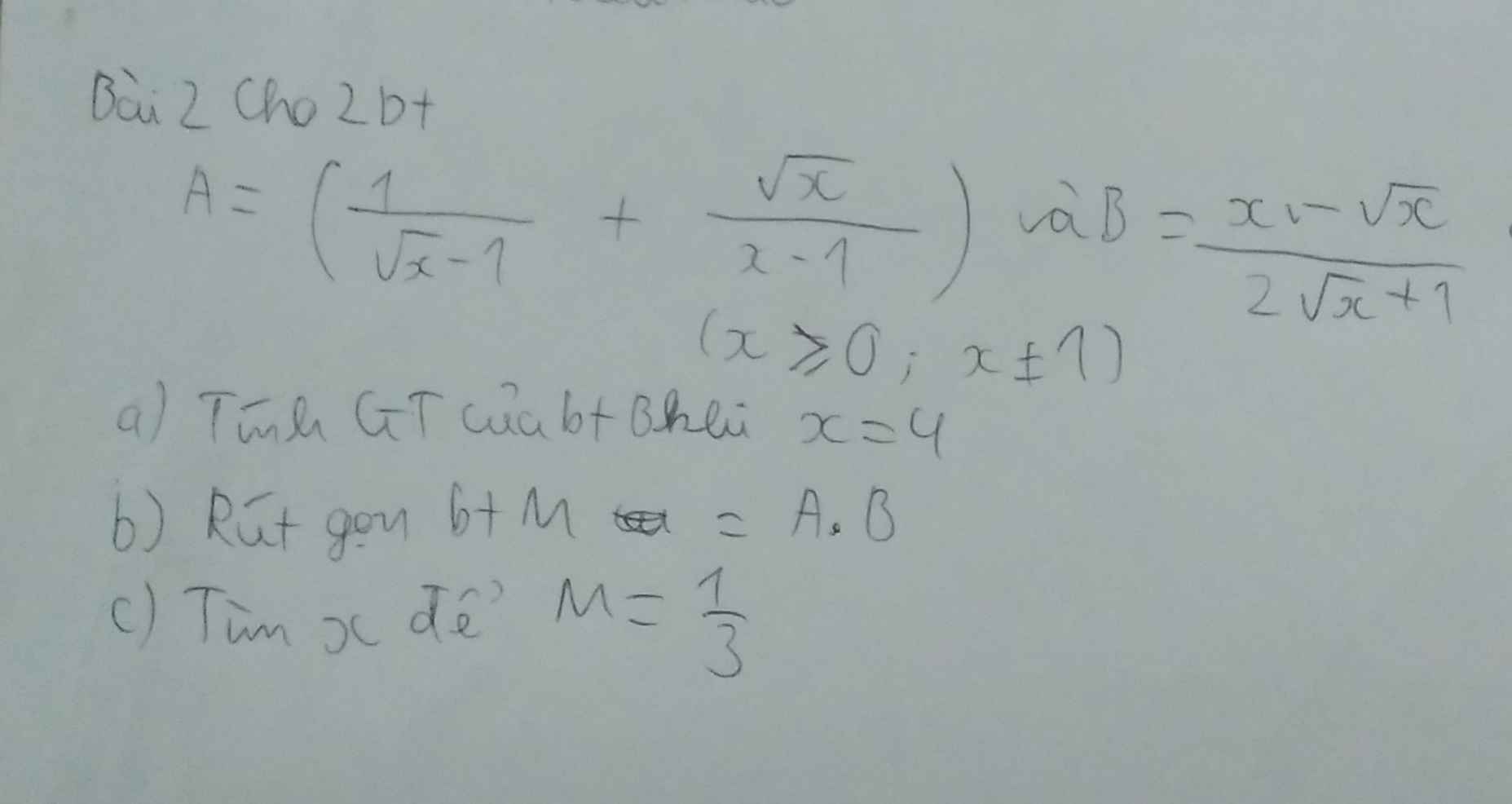
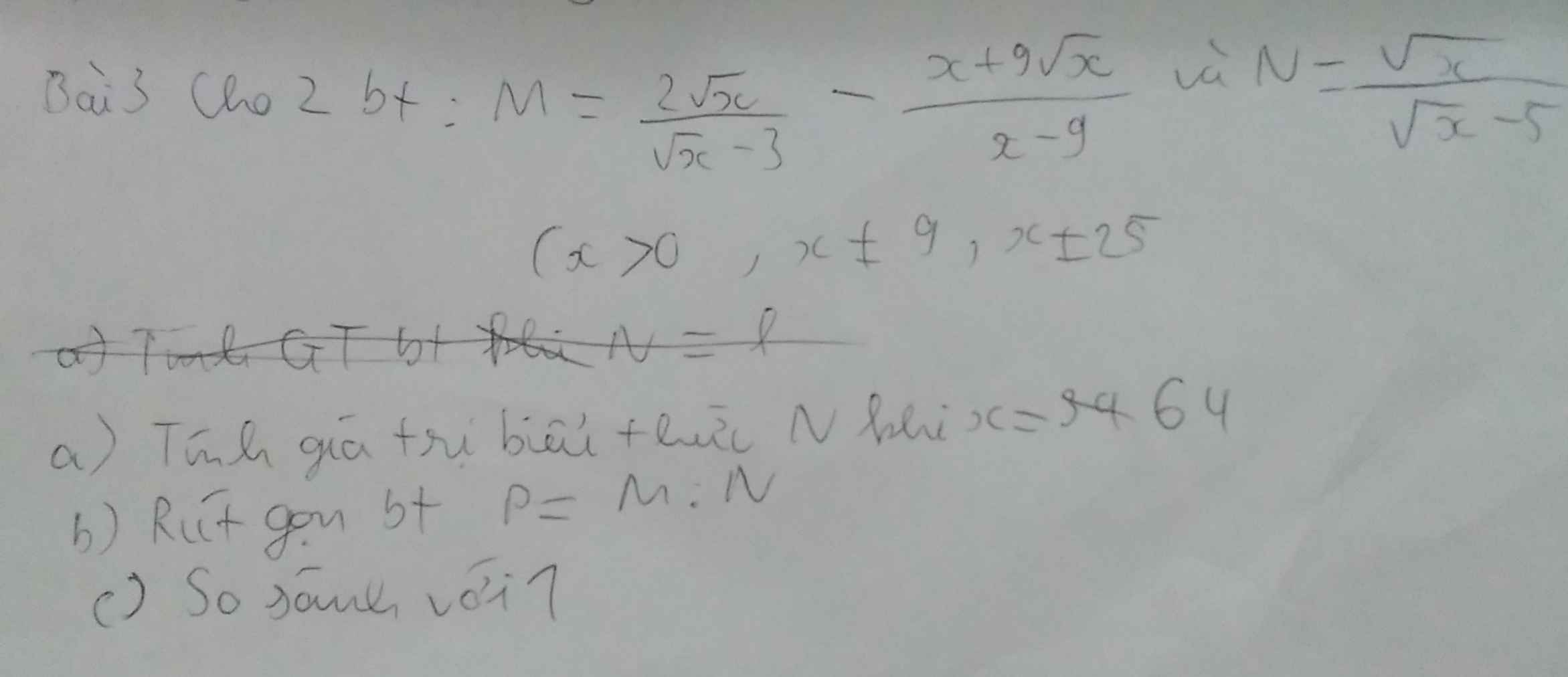
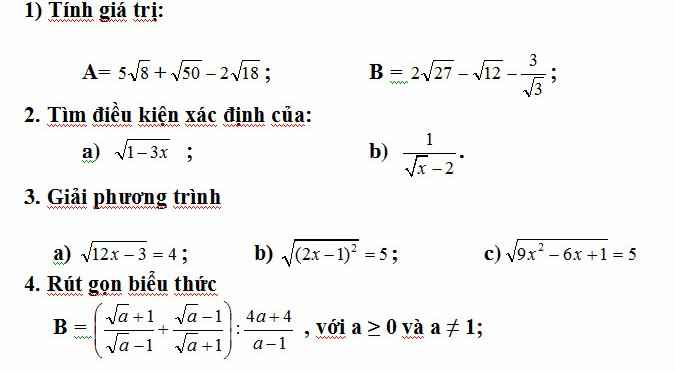
Bài 1:
a.
$=4\sqrt{7}+4\sqrt{2}-4\sqrt{7}-3\sqrt{2}=(4\sqrt{7}-4\sqrt{7})+(4\sqrt{2}-3\sqrt{2})=\sqrt{2}$
b.
$=\frac{\sqrt{7}(3-\sqrt{2})}{3-\sqrt{2}}-\frac{3(\sqrt{7}-2)}{(\sqrt{7}+2)(\sqrt{7}-2)}=\sqrt{7}-(\sqrt{7}-2)=2$
Bài 2:
a.
Xanh lá: $(D)$ và xanh dương $(D')$
b. PT hoành độ giao điểm:
$3x+1=\frac{1}{2}x-1$
$\Leftrightarrow x=\frac{-4}{5}$
$y=3x+1=3.\frac{-4}{5}+1=\frac{-7}{5}$
Vậy giao điểm là $(\frac{-4}{5}, \frac{-7}{5})$