
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.







Bài 1:
a) \(R_{tđ}=R_1+R_2=7,5+15=22,5\left(\Omega\right)\)
b) \(I=I_1=I_2=0,3A\)
\(\left\{{}\begin{matrix}U=I.R_{tđ}=0,3.22,5=6,75\left(V\right)\\U_1=I_1.R_1=0,3.7,5=2,25\left(V\right)\\U_2=I_2.R_2=0,3.15=4,5\left(V\right)\end{matrix}\right.\)
Bài 2:
a) Điện trở tương đương:
\(R_{tđ}=R_1+R_2=3+6=9\left(\Omega\right)\)
b) \(I=I_1=I_2=\dfrac{U}{R_{tđ}}=\dfrac{9}{9}=1\left(A\right)\left(R_1ntR_2\right)\)
Hiệu điện thế giữa 2 đầu mỗi điện trở:
\(\left\{{}\begin{matrix}U_1=I_1.R_1=1.3=3\left(V\right)\\U_2=I_2.R_2=1.6=6\left(V\right)\end{matrix}\right.\)

Ảnh ảo, cùng chiều và nhỏ hơn vật.
Khoảng cách từ vật đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{12}=\dfrac{1}{7,2}-\dfrac{1}{d}\)
\(\Rightarrow d=18cm\)

Bài 1:
a, \(\)\(\)\(=>R2//\left[R4nt\left(R3//R5\right)\right]\)
\(=>Rtd=\dfrac{R2\left[R4+\dfrac{R3.R5}{R3+R5}\right]}{R2+R4+\dfrac{R3.R5}{R3+R5}}=\dfrac{1.\left[1+\dfrac{1}{1+1}\right]}{1+1+\dfrac{1}{1+1}}=0,6\left(ôm\right)\)
\(=>I=\dfrac{Uab}{Rtd}=\dfrac{10}{0,6}=\dfrac{50}{3}A=I1\)
\(=>Uab=U2345=10V=U2=U345\)
\(=>I2=\dfrac{U2}{R2}=\dfrac{10}{1}=10A\)
\(=>I345=\dfrac{U345}{R345}=\dfrac{10}{1+\dfrac{1.1}{1+1}}=\dfrac{20}{3}A=I4=I35\)
\(=>U35=I35.R35=\dfrac{20}{3}.\dfrac{1.1}{1+1}=\dfrac{10}{3}V=U3=U5\)
\(=>I3=\dfrac{U3}{R3}=\dfrac{\dfrac{10}{3}}{1}=\dfrac{10}{3}A,\)
\(=>I5=\dfrac{U5}{R5}=\dfrac{10}{3}A\)
b, \(I1=0,1A=Im=I2345\)
\(=>Uab=I2345.R2345=0,1.\dfrac{6\left[8+\dfrac{6.12}{6+12}\right]}{6+8+\dfrac{6.12}{6+12}}=0,4V\)




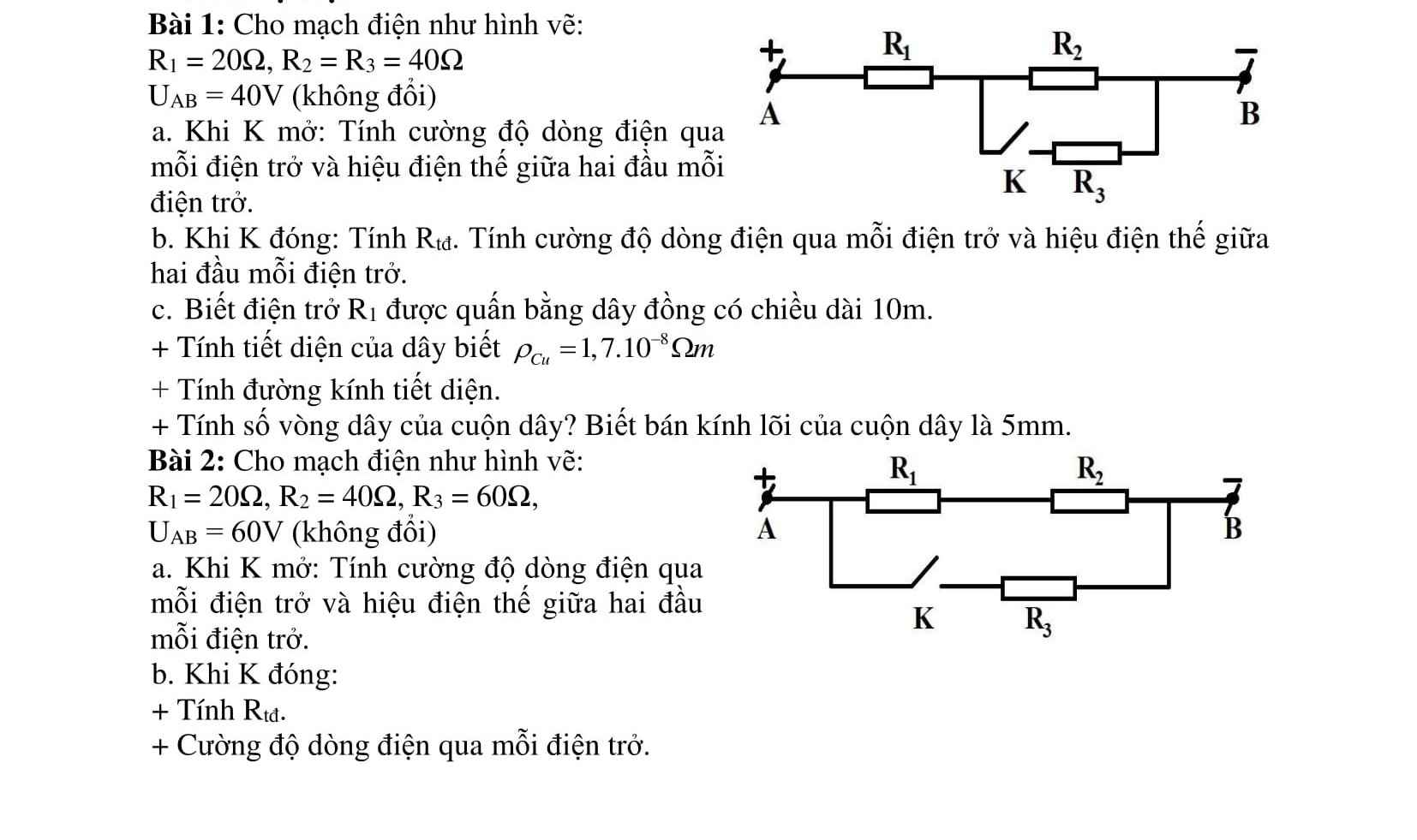
 Giúp mình với ạ,mình đang cần gấp!!!
Giúp mình với ạ,mình đang cần gấp!!!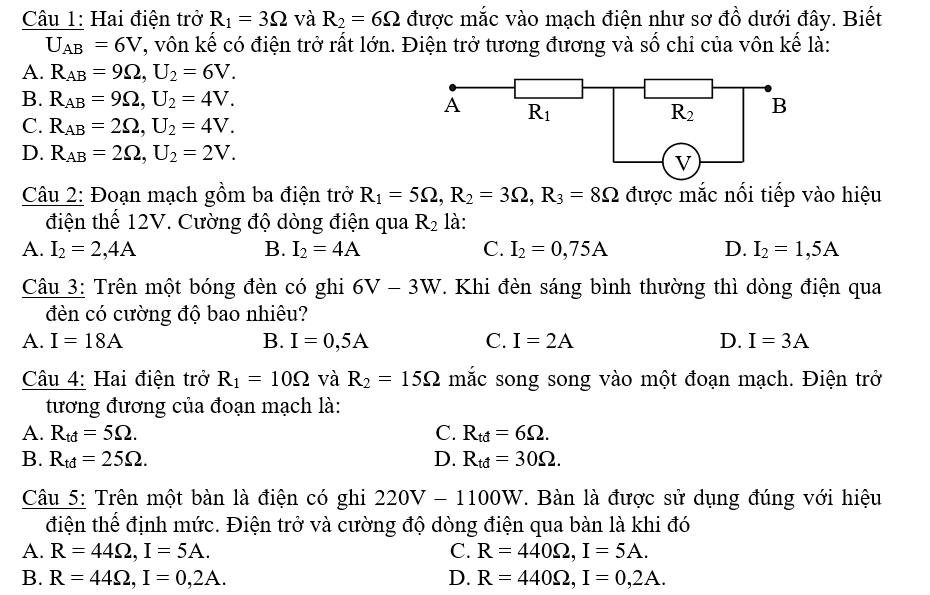




 ai giúp mình bài 3 với ạ, mình đang cần gấp, mình cảm ơn
ai giúp mình bài 3 với ạ, mình đang cần gấp, mình cảm ơn
