
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 2:
a, bạn tự vẽ được nhớ tìm tọa dộ nhé
x 0 0
y 0 0
b, Vì tung độ của điểm nằm trên P có hoành độ bằng 8
=> x = 8
Thay x = 8 vào y = 1/2x^2 ta được :
\(y=\dfrac{1}{2}.64=32\)
Bài 4:
a) Ta có: \(B=\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}+1-\dfrac{2x+\sqrt{x}}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}\left(x\sqrt{x}+1\right)}{x-\sqrt{x}+1}+1-\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}\)
\(=\sqrt{x}\left(\sqrt{x}+1\right)+1-2\sqrt{x}-1\)
\(=x+\sqrt{x}-2\sqrt{x}\)
\(=x-\sqrt{x}\)

Bạn tự vẽ hình nhan với bạn có ghi lộn chỗ MP với tính góc P thành MB với góc B ko nhan nếu lộn thì bài làm như sau:
a/Xét tam giác MNP,góc N=90độ,có:
MP^2=NP^2+MN^2(pytago)
=>NP^2=MP^2-MN^2
NP^2=17^2-8^2
NP^2=225
NP= căn bậc của 225=15
b/ Ta có: sinM=NP/MP=15/17
=> góc M≈62độ
sinP=MN/MP=8/17
=> góc P≈28độ
Sửa đề: MP = 17
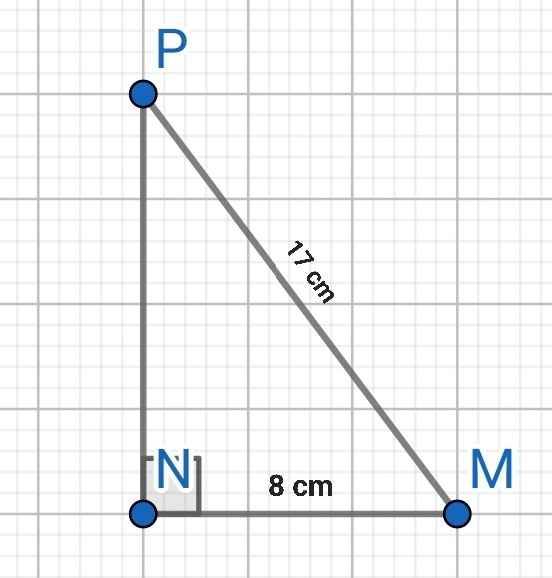 a) MNP vuông tại N
a) MNP vuông tại N
⇒ MP² = MN² + NP² (Pytago)
⇒ NP² = MP² - MN²
= 17² - 8²
= 225
⇒ NP = 15 (cm)
b) Sửa đề: Tính ∠M và ∠P
Ta có:
sin M = NP/MP = 15/17
⇒ ∠M ≈ 62⁰
⇒ ∠P ≈ 90⁰ - ∠M = 90⁰ - 62⁰ = 28⁰


Gọi x là chiều cao của tam giác ; y là cạnh đáy của tam giác (x,y > 0 )
* chiều cao bằng 3/4 đáy:
x = 3/4y
=> x - 3/4y = 0 (1)
* Nếu chiều cao tăng thêm...tăng thêm 9m^2:
1/2(y-2)(x+3) = 1/2xy + 9 (sau đó bạn tự giải phương trình nha) (2)
Từ (1),(2) suy ra chiều cao là 12m , cạnh đáy là 16m

a) Xét \(\left(O\right):\)
+) Ta có: Dây AB = Dây AC (\(\Delta ABC\) cân tại A).
\(\Rightarrow\stackrel\frown{AB}=\stackrel\frown{AC}.\)
+) \(\widehat{ABM}=\dfrac{1}{2}sđ\stackrel\frown{AB}\) (Góc tạo bởi tia tiếp tuyến và dây cung).
\(\widehat{ABC}=\dfrac{1}{2}sđ\stackrel\frown{AC}\) (Góc nội tiếp).
Mà \(\stackrel\frown{AB}=\stackrel\frown{AC}\left(cmt\right).\)
\(\Rightarrow\widehat{ABM}=\widehat{ABC}.\)
\(\Rightarrow\) BA là phân giác \(\widehat{CBM}.\)
b) Xét \(\left(O\right):\)
\(\widehat{MBA}=\dfrac{1}{2}sđ\stackrel\frown{AB}\) (Góc tạo bởi tia tiếp tuyến và dây cung).
\(\widehat{MDB}=\dfrac{1}{2}sđ\stackrel\frown{AB}\) (Góc nội tiếp).
\(\Rightarrow\widehat{MBA}=\widehat{MDB}.\)
Xét \(\Delta MAB\) và \(\Delta MBD:\)
\(\widehat{MBA}=\widehat{MDB}.\)
\(\widehat{BMD}chung.\)
\(\Rightarrow\Delta MAB\sim\Delta MBD\left(g-g\right).\)
\(\Rightarrow\dfrac{MA}{MB}=\dfrac{MB}{MD}\) (Cặp cạnh tương ứng tỉ lệ).
\(\Rightarrow MA.MD=MB^2.\)

\(a,\) Ta có \(\dfrac{1}{\sqrt{n-1}+\sqrt{n}}\)
\(=\dfrac{\sqrt{n-1}-\sqrt{n}}{\left(\sqrt{n-1}+\sqrt{n}\right)\left(\sqrt{n-1}-\sqrt{n}\right)}\\ =\dfrac{\sqrt{n-1}-\sqrt{n}}{n-1-n}=\sqrt{n}-\sqrt{n-1}\)
Thay vào A
\(A=\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+...+\dfrac{1}{\sqrt{n-1}+\sqrt{n}}\\ A=\sqrt{2}-1+\sqrt{3}-\sqrt{2}+...+\sqrt{n}-\sqrt{n-1}\\ A=\sqrt{n}-1\)
\(b,\) Ta có \(\dfrac{1}{\sqrt{n-1}-\sqrt{n}}=\dfrac{\sqrt{n-1}+\sqrt{n}}{\left(\sqrt{n-1}-\sqrt{n}\right)\left(\sqrt{n-1}+\sqrt{n}\right)}\)
\(=\dfrac{\sqrt{n-1}+\sqrt{n}}{n-1-n}=-\sqrt{n-1}-\sqrt{n}\)
Thay vào B
\(B=\dfrac{1}{\sqrt{1}-\sqrt{2}}-\dfrac{1}{\sqrt{2}-\sqrt{3}}-...-\dfrac{1}{\sqrt{24}-\sqrt{25}}\\ B=-1-\sqrt{2}-\left(-\sqrt{2}-\sqrt{3}\right)-...-\left(-\sqrt{24}-\sqrt{25}\right)\\ B=-1-\sqrt{2}+\sqrt{2}+\sqrt{3}-\sqrt{3}-\sqrt{4}+...+\sqrt{24}+\sqrt{25}\\ B=\sqrt{25}-1\)

\(a,\Leftrightarrow m-1>0\Leftrightarrow m>1\\ b,m=2\Leftrightarrow y=x+1\)
Bạn tự vẽ đi
\(c,\) PT hoành độ giao điểm: \(\left(m-1\right)x+2m-3=2x+1\)
Mà 2 đt cắt nhau tại 1 điểm trên trục tung nên x=0
\(\Leftrightarrow2m-3=1\\ \Leftrightarrow m=2\)
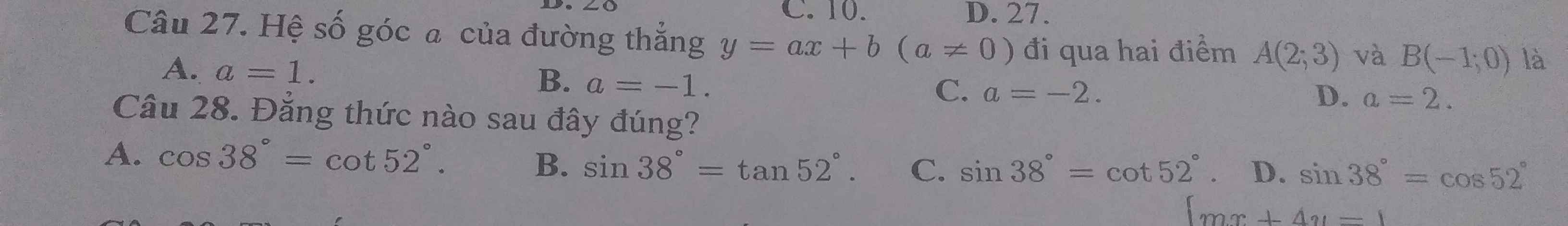
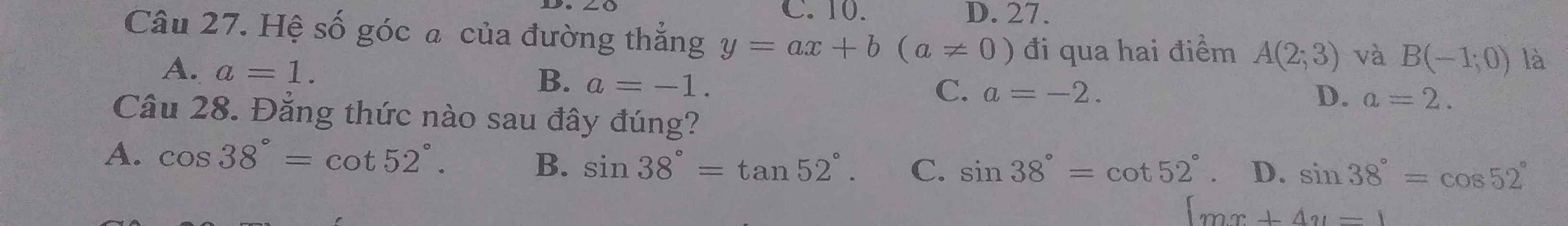
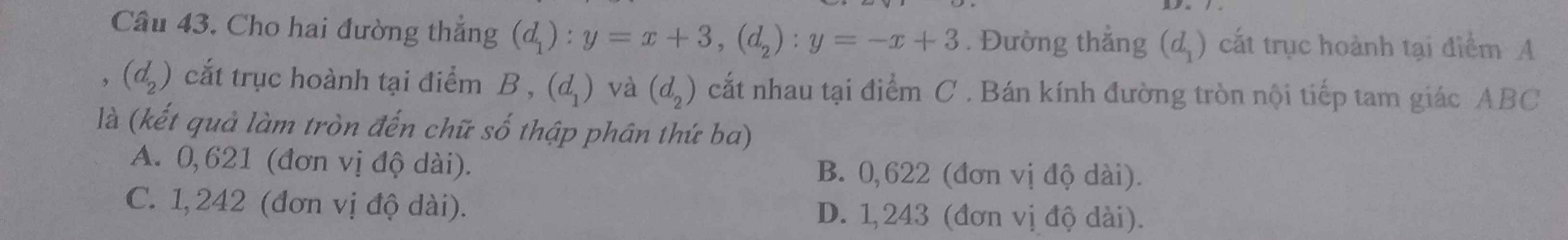
 mọi người giúp mình giải câu 2 3 4 và phần hình học vs ạ. mình cảm ơnnnnnnnnnnnnn
mọi người giúp mình giải câu 2 3 4 và phần hình học vs ạ. mình cảm ơnnnnnnnnnnnnn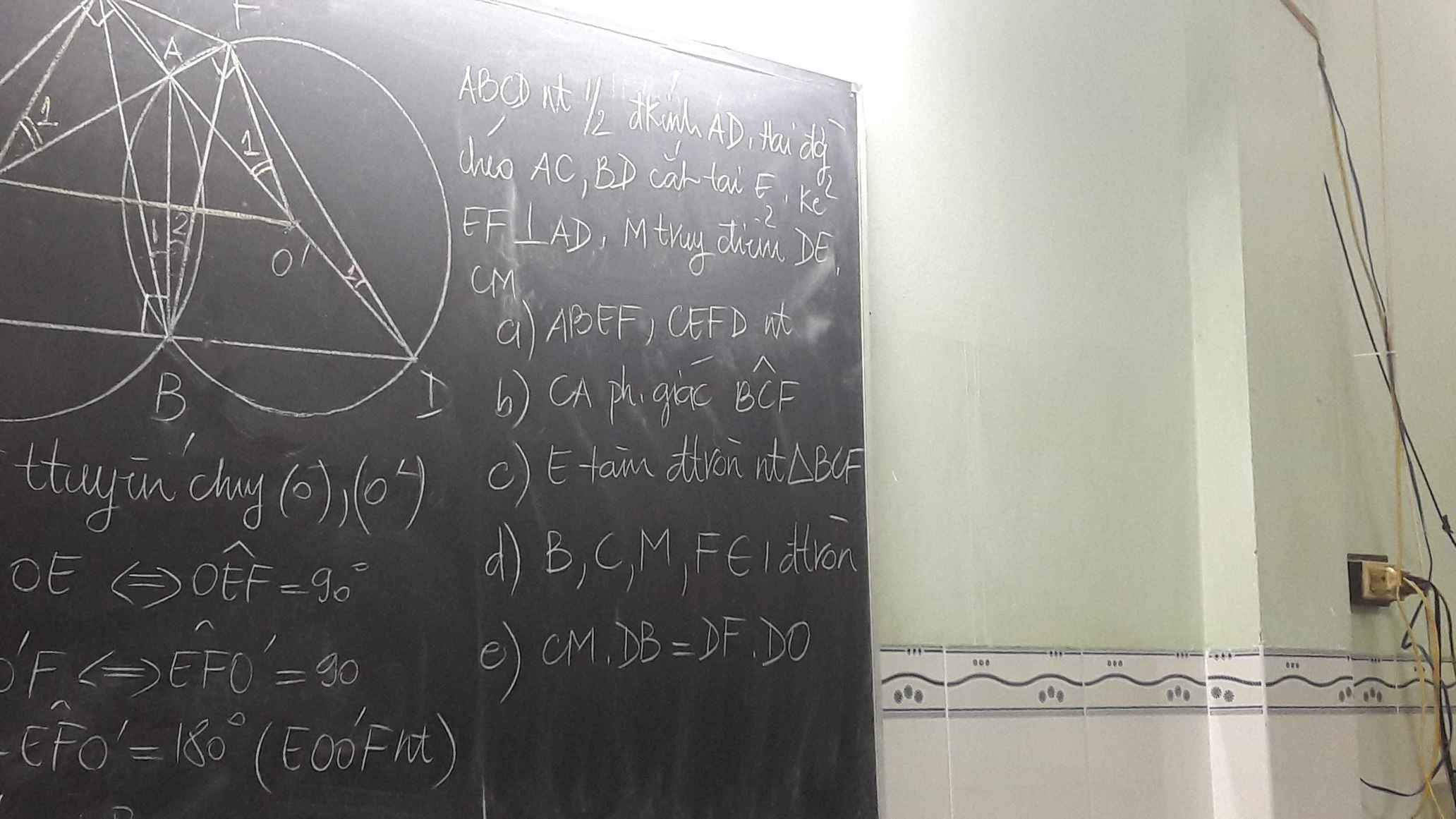


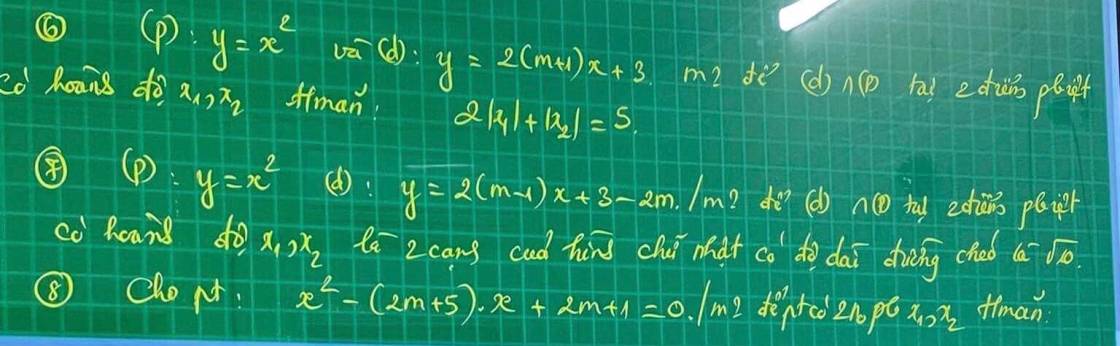



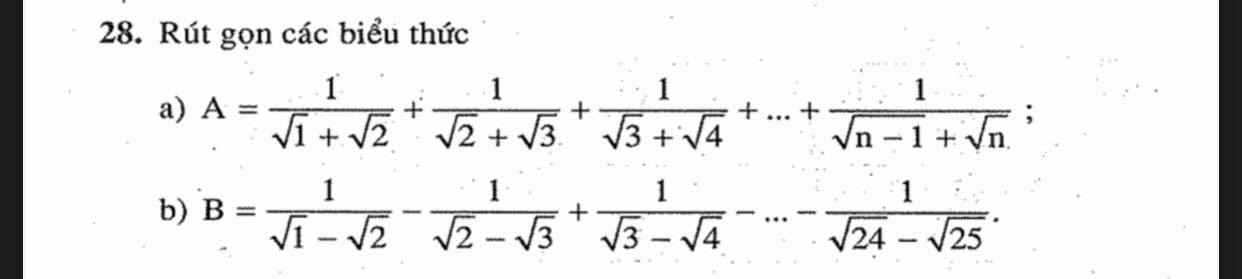

28D
27: Theo đề, ta có hệ:
\(\left\{{}\begin{matrix}a\cdot2+b=3\\a\cdot\left(-1\right)+b=0\end{matrix}\right.\Leftrightarrow a=1\)
=>Chọn A
43:
tọa độ A là;
y=0 và x+3=0
=>A(-3;0)
Tọa độ B là;
-x+3=0 và y=0
=>B(3;0)
Tọa độ C là;
x+3=-x+3 và y=x+3
=>x=0 và y=3
=>C(0;3)
A(-3;0); B(3;0); C(0;3)
\(AB=\sqrt{\left(3+3\right)^2+\left(0-0\right)^2}=6\)
\(AC=\sqrt{\left(0+3\right)^2+\left(3-0\right)^2}=3\sqrt{2}\)
BC=căn (0-3)^2+(3-0)^2=3*căn 2(cm)
Vì BC^2+AC^2=AB^2 và BC=AC
nên ΔABC vuông cân tại B
P=1/2(3căn 2+3căn 2+6)=3căn 2+3(cm)
S=1/2*3*căn 2*3*căn 2=9
=>r=9/3căn 2+3=-3+3căn 2=1,243
=>Chọn D