
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mọi người giúp mình với mình đang cần gấp mình cảm ơn nhiều ạ

Lời giải:
a. Khi $x=64$ thì: $Q=\frac{\sqrt{64}-2}{\sqrt{64}-3}=\frac{8-2}{8-3}=\frac{6}{5}$
b.
\(P=\frac{x}{(\sqrt{x}-2)(\sqrt{x}+2)}+\frac{\sqrt{x}+2}{(\sqrt{x}-2)(\sqrt{x}+2)}+\frac{\sqrt{x}-2}{(\sqrt{x}+2)(\sqrt{x}-2)}\)
\(=\frac{x+\sqrt{x}+2+\sqrt{x}-2}{(\sqrt{x}+2)(\sqrt{x}-2)}=\frac{x+2\sqrt{x}}{(\sqrt{x}+2)(\sqrt{x}-2)}=\frac{\sqrt{x}(\sqrt{x}+2)}{(\sqrt{x}-2)(\sqrt{x}+2)}=\frac{\sqrt{x}}{\sqrt{x}-2}\)
Ta có đpcm.
c. \(K=Q(P-1)=\frac{\sqrt{x}-2}{\sqrt{x}-3}.(\frac{\sqrt{x}}{\sqrt{x}-2}-1)=\frac{\sqrt{x}-2}{\sqrt{x}-3}.\frac{2}{\sqrt{x}-2}=\frac{2}{\sqrt{x}-3}\)
$K=m+1$
$\Leftrightarrow \frac{2}{\sqrt{x}-3}=m+1$
$\Leftrightarrow m=\frac{2}{\sqrt{x}-3}-1$
Với $m=0$ (stn nhỏ nhất) thì $\frac{2}{\sqrt{x}-3}-1=m$ có nghiệm $x=25$
Vậy stn $m$ cần tìm là $0$

a. PTHDGD: \(\dfrac{2}{5}x-\dfrac{4}{3}=x+2\Leftrightarrow\dfrac{3}{5}x=-\dfrac{10}{3}\Leftrightarrow x=-\dfrac{50}{9}\Leftrightarrow y=-\dfrac{32}{9}\Leftrightarrow A\left(-\dfrac{50}{9};-\dfrac{32}{9}\right)\)
Vậy \(A\left(-\dfrac{50}{9};-\dfrac{32}{9}\right)\) là tọa độ giao điểm
b. PTHDGD: \(x-2=3x+4\Leftrightarrow x=-3\Leftrightarrow y=-5\Leftrightarrow B\left(-3;-5\right)\)
Vậy \(B\left(-3;-5\right)\) là tọa độ giao điểm

3: \(\left(\dfrac{1}{\sqrt{2}-1}-\dfrac{1}{\sqrt{2}+1}\right):\sqrt{3-2\sqrt{2}}\)
\(=\dfrac{\sqrt{2}+1-\sqrt{2}+1}{2-1}:\left(\sqrt{2}-1\right)\)
\(=\dfrac{2}{\sqrt{2}-1}=2\left(\sqrt{2}+1\right)=2\sqrt{2}+2\)
5:
\(\dfrac{\sqrt{5}+\sqrt{3}}{\sqrt{5}-\sqrt{3}}+\dfrac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}\)
\(=\dfrac{\left(\sqrt{5}+\sqrt{3}\right)^2+\left(\sqrt{5}-\sqrt{3}\right)^2}{\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)}\)
\(=\dfrac{8+2\sqrt{15}+8-2\sqrt{15}}{2}=\dfrac{16}{2}=8\)
6:
\(\dfrac{\sqrt{5}-1}{\sqrt{5}+1}-\dfrac{\sqrt{5}+1}{\sqrt{5}-1}\)
\(=\dfrac{\left(\sqrt{5}-1\right)^2-\left(\sqrt{5}+1\right)^2}{\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)}\)
\(=\dfrac{6-2\sqrt{5}-6-2\sqrt{5}}{4}=\dfrac{-4\sqrt{5}}{4}=-\sqrt{5}\)
4:
\(\dfrac{6}{\sqrt{2}-\sqrt{3}+3}\)
\(=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{\left(\sqrt{2}-\sqrt{3}-3\right)\left(\sqrt{2}-\sqrt{3}+3\right)}\)
\(=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{5-2\sqrt{6}-9}=\dfrac{-6\left(\sqrt{2}-\sqrt{3}-3\right)}{4+2\sqrt{6}}\)
\(=\dfrac{-3\left(\sqrt{2}-\sqrt{3}-3\right)}{\sqrt{6}+2}=\dfrac{-3\left(\sqrt{2}-\sqrt{3}-3\right)\left(\sqrt{6}-2\right)}{2}\)
\(=\dfrac{-3\left(2\sqrt{3}-2\sqrt{2}-3\sqrt{2}+2\sqrt{3}-6\sqrt{3}+6\right)}{2}\)
\(=\dfrac{-3\left(-2\sqrt{3}-5\sqrt{2}+6\right)}{2}\)

a, Vì ME là tiếp tuyến đường tròn O và M là tiếp điểm
=> \(MO\perp MF\) ( t/c tiếp tuyến ) hay ^OME = 900
Vậy tam giác EMO là tam giác vuông tại M
b, mình sửa đề là OE = 60 cm nhé
Theo định lí Pytago cho tam giác EMO vuông tại M
\(ME=\sqrt{EO^2-OM^2}=48\)cm
c, sửa ON vuông OE tại N
đến đây thì mình chả hiểu đề kiểu gì, chịu, bạn chép đề kiểu gì ấy, sai tào lao sao á, xem lại nhé
a: Xét ΔMEO có \(\widehat{OME}=90^0\)
nên ΔMEO vuông tại M

Bài 3:
a:Ta có: \(\sqrt{4x^2-4x+1}=3\)
\(\Leftrightarrow\left|2x-1\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=3\\2x-1=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
b: Ta có: \(2\sqrt{x-1}-4=0\)
\(\Leftrightarrow x-1=4\)
hay x=5


Câu 4:
D và F cùng nhìn AC dưới 1 góc vuông nên tứ giác ACDF nội tiếp
\(\Rightarrow\widehat{ADF}=\widehat{ACF}\) (cùng chắn AF)
Tương tự, ABDE nội tiếp \(\Rightarrow\widehat{ABE}=\widehat{ADE}\) (cùng chắn AE)
Lại có \(\widehat{ABE}=\widehat{ACF}\) (cùng phụ góc \(\widehat{A}\))
\(\Rightarrow\widehat{ADE}=\widehat{ADF}\) hay AD là phân giác góc \(\widehat{FDE}\)
./
Hoàn toàn tương tự, ta cũng có CF là phân giác \(\widehat{DFE}\Rightarrow\widehat{BFD}=\widehat{AFE}\)
Mà \(\widehat{AFE}=\widehat{BFK}\Rightarrow\widehat{BFK}=\widehat{BFD}\)
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{FK}{FD}\) theo định lý phân giác
Đồng thời \(\dfrac{CK}{CD}=\dfrac{FK}{FD}\) (CF là phân giác ngoài góc \(\widehat{DFK}\))
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{CK}{CD}\Rightarrow\dfrac{BK}{CK}=\dfrac{BD}{CD}\)
Qua B kẻ đường thẳng song song AC cắt AK và AD tại P và Q
Theo Talet: \(\dfrac{BK}{CK}=\dfrac{BP}{AC}\) đồng thời \(\dfrac{BD}{DC}=\dfrac{BQ}{AC}\)
\(\Rightarrow\dfrac{BP}{AC}=\dfrac{BQ}{AC}\Rightarrow BP=BQ\)
Mặt khác BP song song MF (cùng song song AC)
\(\Rightarrow\dfrac{MF}{BP}=\dfrac{AF}{AB}\) ; \(\dfrac{NF}{BQ}=\dfrac{AF}{AB}\) (Talet)
\(\Rightarrow\dfrac{MF}{BP}=\dfrac{NF}{BQ}\Rightarrow MF=NF\)



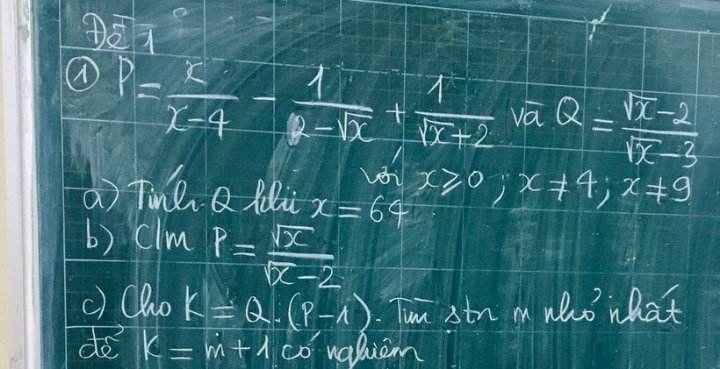 giúp mình câu c với ạ, mình cảm ơn nhiều
giúp mình câu c với ạ, mình cảm ơn nhiều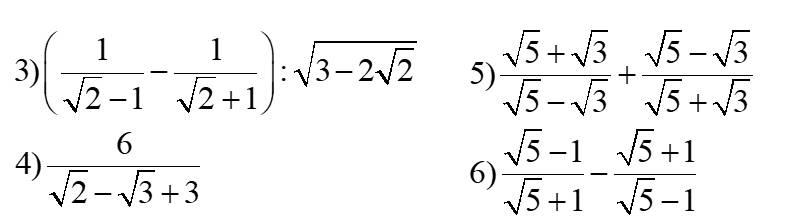

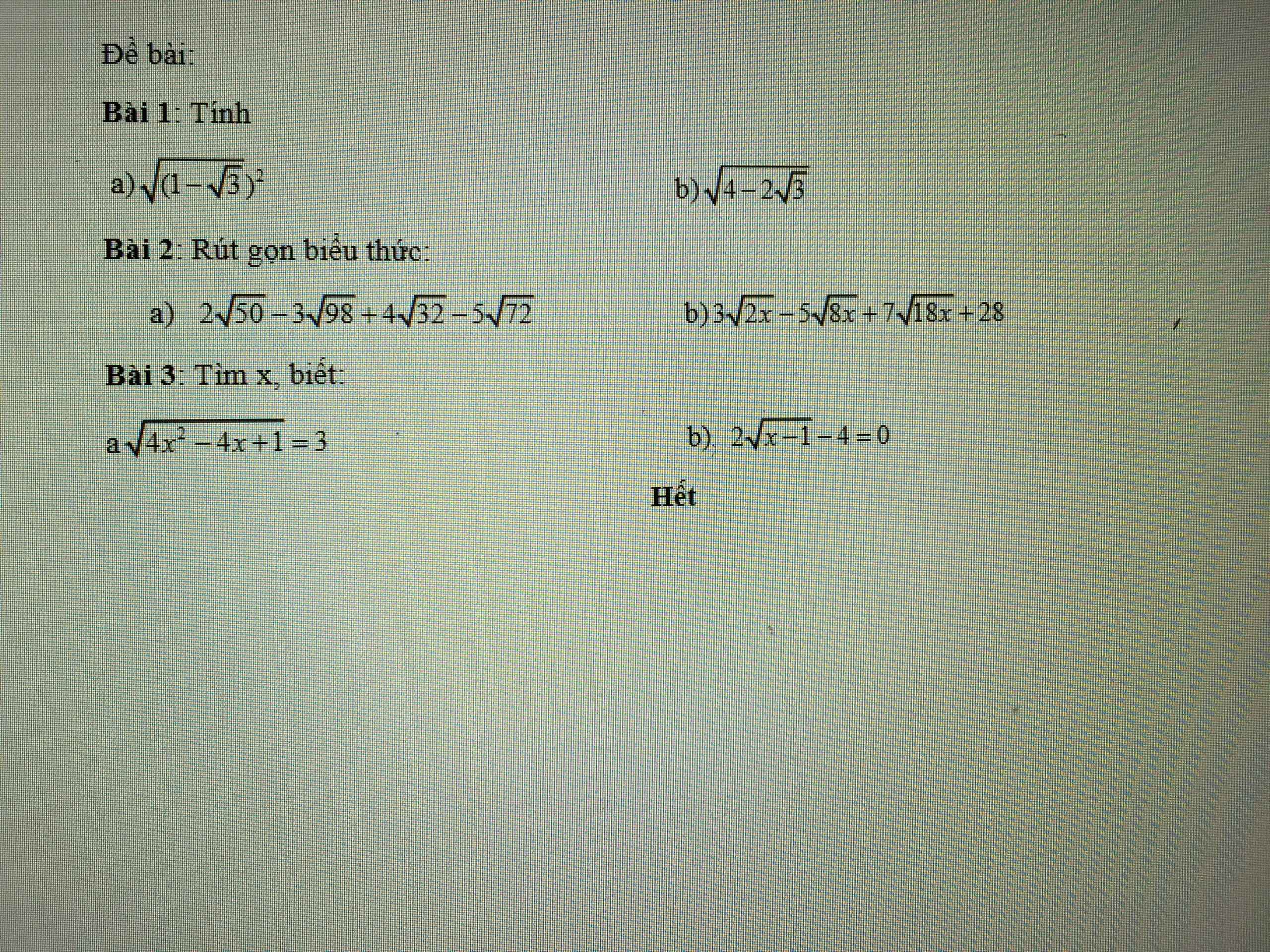 Giúp mình vs ạ. Cảm ơn trước ạ!
Giúp mình vs ạ. Cảm ơn trước ạ!


a) Xét \(\left(O\right):\)
+) Ta có: Dây AB = Dây AC (\(\Delta ABC\) cân tại A).
\(\Rightarrow\stackrel\frown{AB}=\stackrel\frown{AC}.\)
+) \(\widehat{ABM}=\dfrac{1}{2}sđ\stackrel\frown{AB}\) (Góc tạo bởi tia tiếp tuyến và dây cung).
\(\widehat{ABC}=\dfrac{1}{2}sđ\stackrel\frown{AC}\) (Góc nội tiếp).
Mà \(\stackrel\frown{AB}=\stackrel\frown{AC}\left(cmt\right).\)
\(\Rightarrow\widehat{ABM}=\widehat{ABC}.\)
\(\Rightarrow\) BA là phân giác \(\widehat{CBM}.\)
b) Xét \(\left(O\right):\)
\(\widehat{MBA}=\dfrac{1}{2}sđ\stackrel\frown{AB}\) (Góc tạo bởi tia tiếp tuyến và dây cung).
\(\widehat{MDB}=\dfrac{1}{2}sđ\stackrel\frown{AB}\) (Góc nội tiếp).
\(\Rightarrow\widehat{MBA}=\widehat{MDB}.\)
Xét \(\Delta MAB\) và \(\Delta MBD:\)
\(\widehat{MBA}=\widehat{MDB}.\)
\(\widehat{BMD}chung.\)
\(\Rightarrow\Delta MAB\sim\Delta MBD\left(g-g\right).\)
\(\Rightarrow\dfrac{MA}{MB}=\dfrac{MB}{MD}\) (Cặp cạnh tương ứng tỉ lệ).
\(\Rightarrow MA.MD=MB^2.\)