
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a: \(=14x^3-7x^2+28x-14x^3=-7x^2+28x\)
b: \(=\dfrac{3x^3-6x^2+2x^2-4x-x+2}{x-2}=3x^2+2x-1\)
c: \(\Leftrightarrow\left(2x-3-5x\right)\left(2x-3+5x\right)=0\)
=>(-3x-3)(7x-3)=0
=>x=-1 hoặc x=3/7

1.a) xy + 2y - x2 + 4
= y ( x + 2 ) - ( x2 - 4 ) = y ( x + 2 ) - ( x - 2 ) ( x + 2 ) = ( x + 2 )( y - x + 2 )
b) 2x2 + y2 + 3xy
= ( 2x2 + 2xy ) + ( y2 + xy )
= 2x ( x + y ) + y ( x + y )
= ( x + y ) ( 2x + y )
2.
x - y = 5 \(\Rightarrow\)( x - y )2 = 25 \(\Rightarrow\)x2 + y2 = 25 + 2xy = 25 + 2.3 = 31
A = ( x + y )2 = x2 + y2 + 2xy = 31 + 6 = 37

Lời giải:
ĐKXĐ: $x\neq \pm 3; x\neq 0$
a. \(A=\left[\frac{-(x-3)}{x+3}.\frac{(x+3)^2}{(x-3)(x+3)}+\frac{x}{x+3}\right].\frac{x+3}{3x^2}\)
\(=\left(-1+\frac{x}{x+3}\right).\frac{x+3}{3x^2}=\frac{-3}{x+3}.\frac{x+3}{3x^2}=\frac{-1}{x^2}\)
b. Với $x=\frac{-1}{2}$ thì $x^2=\frac{1}{4}$
$\Rightarrow A=\frac{-1}{\frac{1}{4}}=-4$
c.
Với $x\neq 0, \pm 3$ thì $\frac{1}{x^2}>0\Leftrightarrow A=\frac{-1}{x^2}< 0$ với mọi $x\neq 0; x\neq \pm 3$
a) Ta có: \(A=\left(\dfrac{3-x}{x+3}\cdot\dfrac{x^2+6x+9}{x^2-9}+\dfrac{x}{x+3}\right):\dfrac{3x^2}{x+3}\)
\(=\left(\dfrac{-\left(x-3\right)}{x+3}\cdot\dfrac{\left(x+3\right)^2}{\left(x+3\right)\left(x-3\right)}+\dfrac{x}{x+3}\right):\dfrac{3x^2}{x+3}\)
\(=\left(\dfrac{-x-3+x}{x+3}\right)\cdot\dfrac{x+3}{3x^2}\)
\(=-\dfrac{1}{x^2}\)

\(=2x^2\left(x-1\right)-4x\left(x-1\right)=\left(x-1\right)\left(2x^2-4x\right)=2x\left(x-2\right)\left(x-1\right)\)

b: \(A=\dfrac{x^2+2+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{1}{x^2+x+1}\)

2:
b: Khi x=-3 thì (1) sẽ là -3(m-1)+2m+5=0
=>-3m+3+2m+5=0
=>8-m=0
=>m=8
c: Để ptvn thì m-1=0
=>m=1

\(3x\left(x-1\right)+2\left(1-x\right)=0.\)
\(\Leftrightarrow3x\left(x-1\right)-2\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(3x-2\right)=0\)
\(\Rightarrow x=1\) hoặc \(x=\frac{2}{3}\)


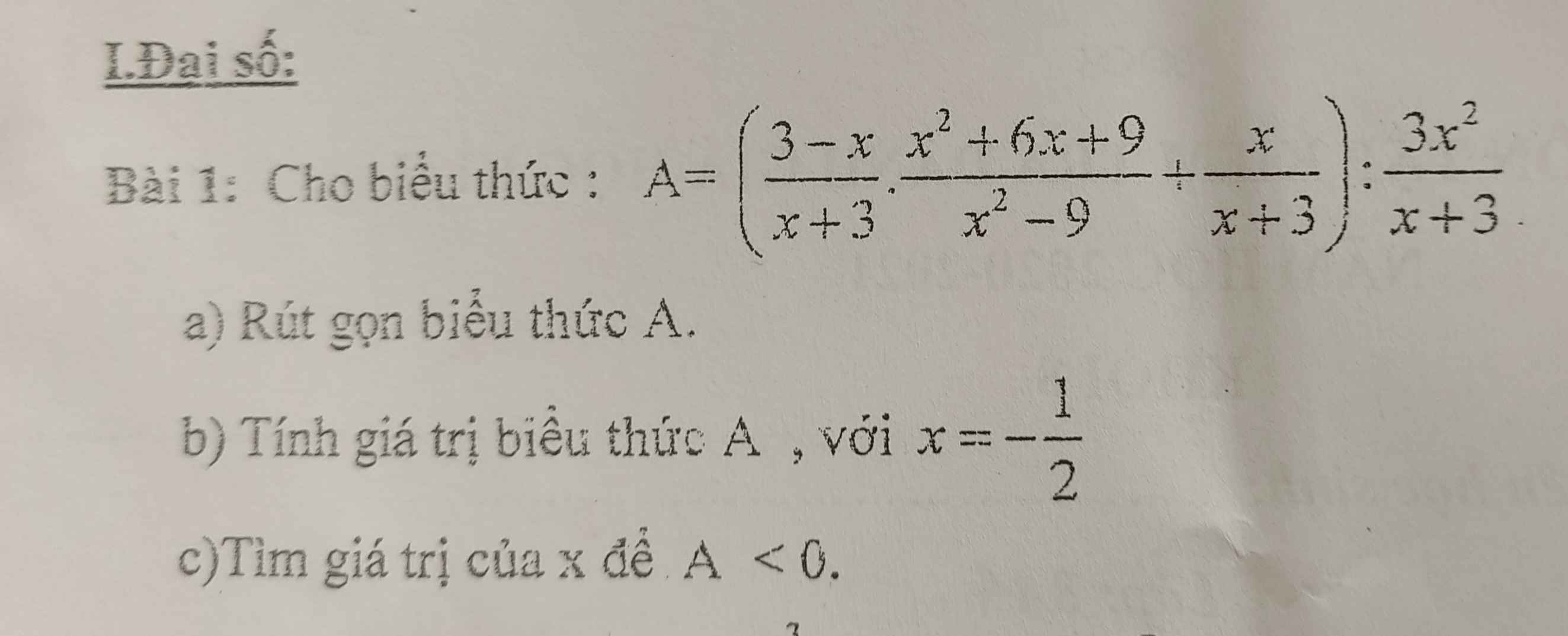


Bài 1:
a: Ta có: \(5x^2-\left(2x+1\right)\left(x-2\right)-x\left(3x+3\right)+7\)
\(=5x^2-2x^2+4x-x+2-3x^2-3x+7\)
=9
b: Ta có: \(\left(3x-1\right)\left(2x+3\right)-\left(x-5\right)\left(6x-1\right)-38x\)
\(=6x^2+9x-2x-3-\left(6x^2-x-30x+5\right)-38x\)
\(=6x^2-31x-3-6x^2+31x-5\)
=-8