K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
mn giúp mình bài 3 vs ạ. Mình cảm ơn nhiều
5 tháng 7 2021
Xét pt hoành độ gđ của đường thẳng và parabol có:
\(\left(m-1\right)x^2+3mx+2m=2x-1\)
\(\Leftrightarrow\left(m-1\right)x^2+x\left(3m-2\right)+2m+1=0\) (1)
Để đt và parabol cắt tại hai điểm pb có hoành độ âm
\(\Leftrightarrow\) Pt (1) có hai nghiệm âm phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\S< 0\\P>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m^2-8m+8>0\\\dfrac{2-3m}{m-1}< 0\\\dfrac{2m+1}{m-1}>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\in\left(-\infty;4-2\sqrt{2}\right)\cup\left(4+2\sqrt{2};+\infty\right)\\m\in\left(-\infty;\dfrac{2}{3}\right)\cup\left(1;+\infty\right)\\m\in\left(-\infty;-\dfrac{1}{2}\right)\cup\left(1;+\infty\right)\end{matrix}\right.\)
\(\Rightarrow m\in\left(-\infty;-\dfrac{1}{2}\right)\cup\left(4+2\sqrt{2};+\infty\right)\)
Vậy...
PK
5
TA
18 tháng 5 2021
`sin3x sinx+sin(x-π/3) cos (x-π/6)=0`
`<=> 1/2 (cos2x - cos4x) + 1/2(-sin π/6 + sin (2x-π/2)=0`
`<=> cos2x-cos4x-1/2+ sin(2x-π/2)=0`
`<=>cos2x-cos4x-1/2+ sin2x .cos π/2 - cos2x. sinπ/2=0`
`<=> cos2x - cos4x - cos2x = 1/2`
`<=> cos4x = cos(2π)/3`
`<=>` \(\left[{}\begin{matrix}4x=\dfrac{2\text{π}}{3}+k2\text{π}\\4x=\dfrac{-2\text{π}}{3}+k2\text{π}\end{matrix}\right.\)
`<=>` \(\left[{}\begin{matrix}x=\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\\x=-\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\end{matrix}\right.\)
NP
0
5 tháng 7 2021
- Xét : \(x^2+8x-20\le0\)
\(\Rightarrow-10\le x\le2\)
Mà \(x>0\)
\(\Rightarrow0< x\le2\)
- Xét \(x^2-2\left(m+3\right)x+m^2-2m< 0\)
Có : \(\Delta^,=b^{,2}-ac=\left(m+3\right)^2-\left(m^2-2m\right)\)
\(=m^2+6m+9-m^2+2m=8m+9\)
- Để bất phương trình có nghiệm
\(\Leftrightarrow\Delta>0\)
\(\Leftrightarrow m>-\dfrac{9}{8}\)
=> Bất phương trình có nghiệm \(S=\left(x_1;x_2\right)\)
Mà \(0< x\le2\)
\(\Rightarrow0< x_1< x_2\le2\)
\(TH1:x=2\)
\(\Rightarrow4-4\left(m+3\right)+m^2-2m< 0\)
\(\Rightarrow3-\sqrt{17}< m< 3+\sqrt{17}\)
\(TH2:0< x_1< x_2< 2\)
\(\Rightarrow\left\{{}\begin{matrix}m^2-2m>0\\m^2-6m-8>0\\0< 2\left(m+3\right)< 2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< 0\\m>2\end{matrix}\right.\\\left[{}\begin{matrix}m>3+\sqrt{17}\\m< 3-\sqrt{17}\end{matrix}\right.\\-3< m< -2\end{matrix}\right.\)
Vậy \(3-\sqrt{7}< m< 3+\sqrt{7}\)
6 tháng 7 2021
Ban ơi :(( ngay chỗ dấu ngoặc nhọn đầu tiên của TH2 có công thức j k bạn?
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 7 2021
Nếu \(y\le0\Rightarrow\left(y-4\right)^2\ge16>9\left(ktm\right)\Rightarrow y>0\)
Nếu \(x\ge0\Rightarrow\left(x+5\right)^2\ge25>9\left(ktm\right)\Rightarrow x< 0\)
Đặt \(\left\{{}\begin{matrix}-x=a>0\\y=b>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left(a-5\right)^2+\left(b-4\right)^2\le9\\3a+b\ge14\end{matrix}\right.\)
Ta có:
\(14^2\le\left(3a+b\right)^2\le\left(3^2+1\right)\left(a^2+b^2\right)\Rightarrow a^2+b^2\ge\dfrac{196}{10}=\dfrac{98}{5}\)
\(P_{min}=\dfrac{98}{5}\) khi \(\left(a;b\right)=\left(\dfrac{21}{5};\dfrac{7}{5}\right)\) hay \(\left(x;y\right)=\left(-\dfrac{21}{5};\dfrac{7}{3}\right)\)
Lại có:
\(\left(a-5\right)^2+\left(b-4\right)^2\le9\Leftrightarrow a^2+b^2\le10a+8b-32\le\sqrt{\left(10^2+8^2\right)\left(a^2+b^2\right)}-32\)
\(\Rightarrow P\le2\sqrt{41}\sqrt{P}-32\Leftrightarrow P-2\sqrt{41}\sqrt{P}+32\le0\)
\(\Rightarrow\left(\sqrt{P}-3-\sqrt{41}\right)\left(\sqrt{P}-3+\sqrt{41}\right)\le0\) (1)
Do \(P\ge\dfrac{98}{5}\Rightarrow\sqrt{P}-3+\sqrt{41}>0\)
Nên (1) tương đương: \(\sqrt{P}-3-\sqrt{41}\le0\Rightarrow P\le50+6\sqrt{41}\)
\(P_{max}=50+6\sqrt{41}\) khi \(\left(a;b\right)=\left(5+\dfrac{15}{\sqrt{41}};4+\dfrac{12}{\sqrt{41}}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2021
\(2\left(\overrightarrow{IA}+\overrightarrow{AB}\right)+3\left(\overrightarrow{IA}+\overrightarrow{AC}\right)=\overrightarrow{0}\Leftrightarrow5\overrightarrow{IA}+2\overrightarrow{AB}+3\overrightarrow{AC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AI}=\dfrac{2}{5}\overrightarrow{AB}+\dfrac{3}{5}\overrightarrow{AC}\)
\(\overrightarrow{JB}+\overrightarrow{BA}+3\overrightarrow{JB}+3\overrightarrow{BC}=\overrightarrow{0}\Leftrightarrow\overrightarrow{BJ}=-\dfrac{1}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{BC}=-\dfrac{1}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{BA}+\dfrac{3}{4}\overrightarrow{AC}\)
\(=-\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AI}.\overrightarrow{BJ}=\left(\dfrac{2}{5}\overrightarrow{AB}+\dfrac{3}{5}\overrightarrow{AC}\right)\left(-\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\right)\)
\(=-\dfrac{2}{5}AB^2+\dfrac{9}{20}AC^2-\dfrac{3}{10}\overrightarrow{AB}.\overrightarrow{AC}\)
\(=-\dfrac{3}{5}a^2+\dfrac{9}{20}a^2-\dfrac{3}{10}a^2.cos60^0=-\dfrac{3}{10}a^2\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2021
b.
Từ câu a ta có
\(\overrightarrow{AI}=\dfrac{2}{5}\overrightarrow{AB}+\dfrac{3}{5}\overrightarrow{AC}\) (1)
\(\overrightarrow{JA}+3\overrightarrow{JC}=\overrightarrow{0}\Leftrightarrow\overrightarrow{JA}+3\overrightarrow{JA}+3\overrightarrow{AC}=\overrightarrow{0}\Leftrightarrow\overrightarrow{JA}=-\dfrac{3}{4}\overrightarrow{AC}\) (2)
Cộng vế (1) và (2):
\(\overrightarrow{JA}+\overrightarrow{AI}=-\dfrac{3}{4}\overrightarrow{AC}+\dfrac{2}{5}\overrightarrow{AB}+\dfrac{3}{5}\overrightarrow{AC}\)
\(\Leftrightarrow\overrightarrow{JI}=\dfrac{2}{5}\overrightarrow{AB}-\dfrac{3}{20}\overrightarrow{AC}\)
\(\Rightarrow IJ^2=\overrightarrow{JI}^2=\left(\dfrac{3}{5}\overrightarrow{AB}-\dfrac{3}{20}\overrightarrow{AC}\right)^2=\dfrac{9}{25}AB^2+\dfrac{9}{400}AC^2-\dfrac{9}{50}\overrightarrow{AB}.\overrightarrow{AC}\)
\(=\dfrac{9}{25}a^2+\dfrac{9}{400}a^2-\dfrac{9}{50}.a^2.cos60^0=...\)
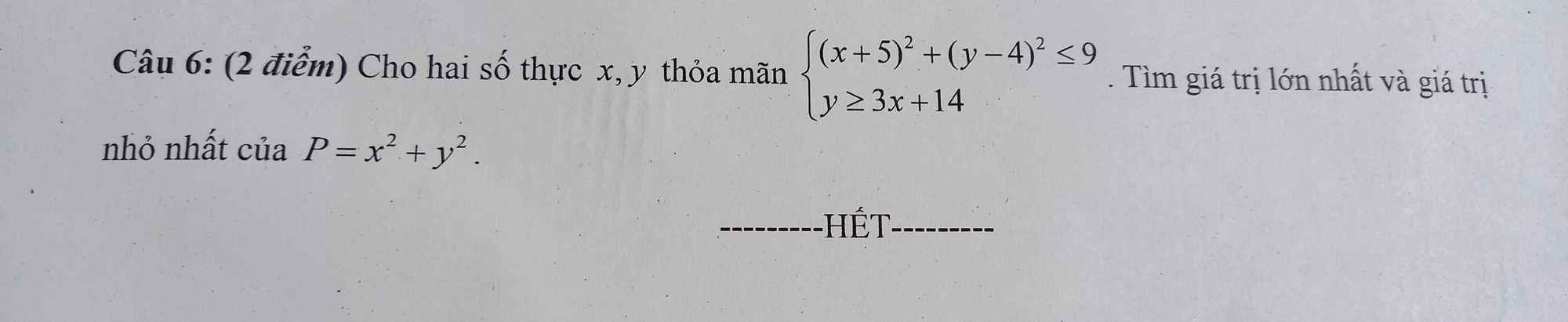
Lời giải:
a.
$|x|\leq 2\Leftrightarrow -2\leq x\leq 2$
Tập $A=[-2;2]$
$(x-1)(x-4)< 0\Leftrightarrow 1< x< 4$
Tập $B=(1;4)$
Đến đây bạn có thể dễ dàng biểu diễn nó trên trục số
b.
$A\cap B=[-2;2]\cap (1;4)=(1;2]$
$A\cup B=[-2;2]\cup (1;4)=[-2;4)$
$A\setminus B= [-2;2]\setminus (1;4)=[-2;1]$