
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng BĐT Bunhiacopxki cho 2 bộ số (\(\sqrt{a+b}\),\(\sqrt{b+c}\),\(\sqrt{a+c}\)) và (1,1,1) có: (1.\(\sqrt{a+b}\)+1.\(\sqrt{b+c}\)+1.\(\sqrt{a+c}\))2 ≤ (a + b + b + c + c + a)(12 + 12 + 12)
=> S2 ≤ 2.3 = 6 ⇔ S ≤ \(\sqrt{6}\)
Dấu "=" xảy ra ⇔ \(\sqrt{a+b}\) = \(\sqrt{b+c}\) = \(\sqrt{a+c}\) ⇔ a +b = b + c = c + a
⇔ 1 - c = 1 - a = 1 - b
⇔ a = b = c = \(\dfrac{1}{3}\)
Vậy maxS = \(\sqrt{6}\) ⇔ a = b = c = \(\dfrac{1}{3}\)

5:
a: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
b: \(MA=\sqrt{OM^2-OA^2}=R\sqrt{3}\)
=>\(AH=\dfrac{R\cdot R\sqrt{3}}{2R}=\dfrac{R\sqrt{3}}{2}\)
=>\(AB=R\sqrt{3}\)

bài 3 :
gọi số xe ban đầu của đội là x(xe)(x>2)
sau khi 2 xe điều động đi làm viêc khác thì số xe còn lại là x-2(xe)
theo dự định cả đôi xe phải vận chuyển 120 tấn hàng
nên mỗi xe ban đầu phải vận chuyển:120/x(tấn hàng)
mỗi xe lúc sau( khi có 2 xe bị điều động đi chỗ khác) phải chuyển
120/x-2(tấn hàng)
vì để hoàn thành công việc mỗi xe còn lại phải chở thêm 2 tấn hàng
=>pt:(120/x-2)-120/x=2
giải pt theo \(\Delta\) ta tìm được x1=12(thỏa mãn)
x2=-10(loại)
vậy lúc đầu trong đội có 12 xe
Câu 4:
a) Xét ΔOAB có OA=OB(=R)
nên ΔOAB cân tại O(Định nghĩa tam giác cân)
Ta có: ΔOAB cân tại O(cmt)
mà OI là đường trung tuyến ứng với cạnh đáy AB(I là trung điểm của AB)
nên OI là đường cao ứng với cạnh AB(Định lí tam giác cân)
hay OI\(\perp\)AB
Ta có: \(\widehat{OIM}=90^0\)(OI\(\perp\)AB)
nên I nằm trên đường tròn đường kính OM(1)
Ta có: \(\widehat{OCM}=90^0\)(gt)
nên C nằm trên đường tròn đường kính OM(2)
Ta có: \(\widehat{ODM}=90^0\)(gt)
nên D nằm trên đường tròn đường kính OM(3)
Từ (1), (2) và (3) suy ra O,I,C,M,D cùng nằm trên một đường tròn(Đpcm)


Bài 36:
a.
Nếu $a,b>0$ thì:
\(A=\frac{\sqrt{a}-\sqrt{b}}{\sqrt{b}}.\frac{\sqrt{a}+\sqrt{b}}{\sqrt{a}}:\frac{a^2-b^2}{ab}\\ =\frac{a-b}{\sqrt{ab}}.\frac{ab}{(a-b)(a+b)}=\frac{\sqrt{ab}}{a+b}\)
Nếu $a,b<0$ thì:
\(A=\frac{\sqrt{-a}-\sqrt{-b}}{\sqrt{-b}}.\frac{\sqrt{-a}+\sqrt{-b}}{\sqrt{-a}}:\frac{a^2-b^2}{ab}\\ =\frac{(-a)-(-b)}{\sqrt{ab}}.\frac{ab}{(a-b)(a+b)}=\frac{\sqrt{ab}}{-(a+b)}\)
Vậy không có đáp án đúng.
b.
$b=1$ thì $b>0, a>0$.
Khi đó: $A=\frac{\sqrt{ab}}{a+b}=2$
$\Leftrightarrow \frac{\sqrt{a}}{a+1}=2$
$\Leftrightarrow \sqrt{a}=2a+2$
$\Leftrightarrow 2a-\sqrt{a}+2=0$
$\Leftrightarrow (\sqrt{a}-0,5)^2+a+1,75=0$
$\Leftrightarrow (\sqrt{a}-0,5)^2+a=-1,75<0$ (vô lý với mọi $a>0$)
Đáp án D.

2:
b: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AH^2=AM\cdot AB\)

a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét ΔACE và ΔAFC có
góc ACE=góc AFC
góc CAE chung
=>ΔACE đồng dạng với ΔAFC
=>AC^2=AE*AF

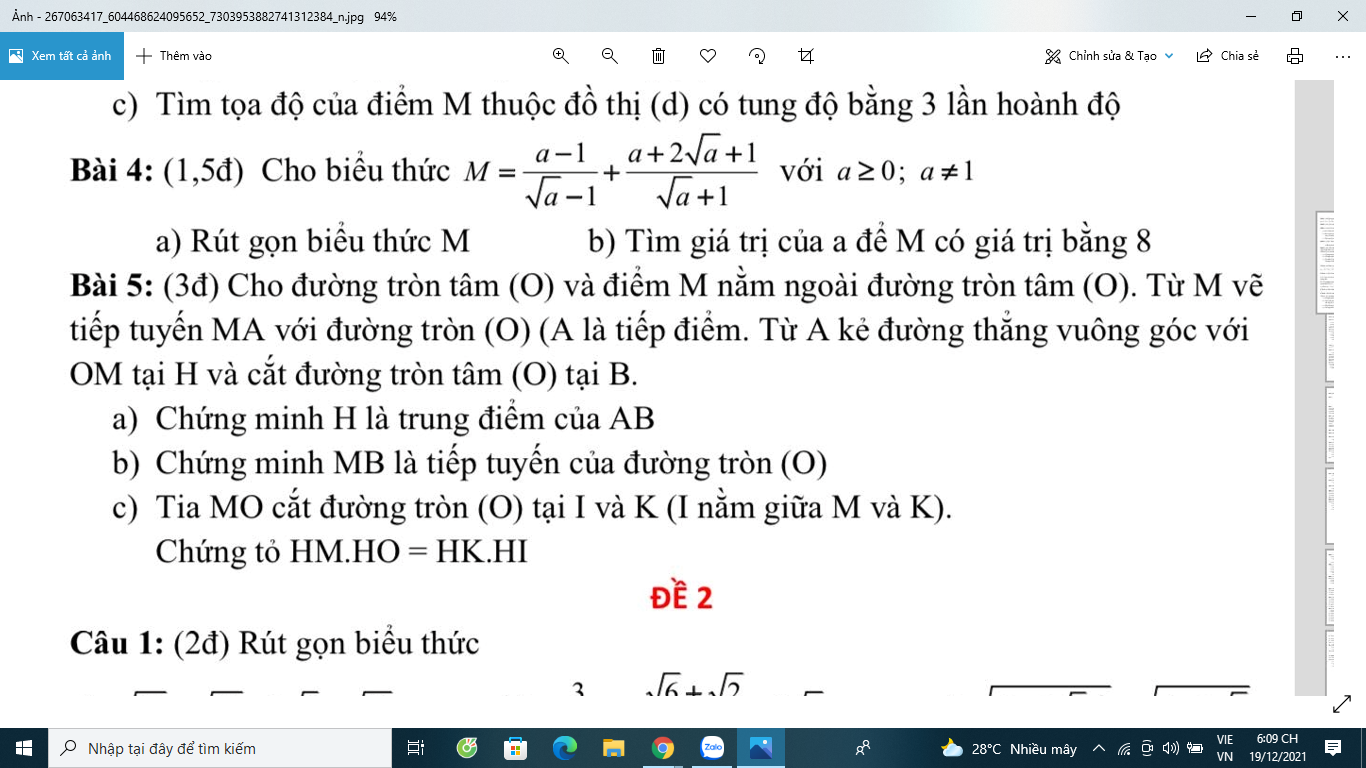



 giúp mình câu b bài 5 vs câu b bài 6 đi
giúp mình câu b bài 5 vs câu b bài 6 đi
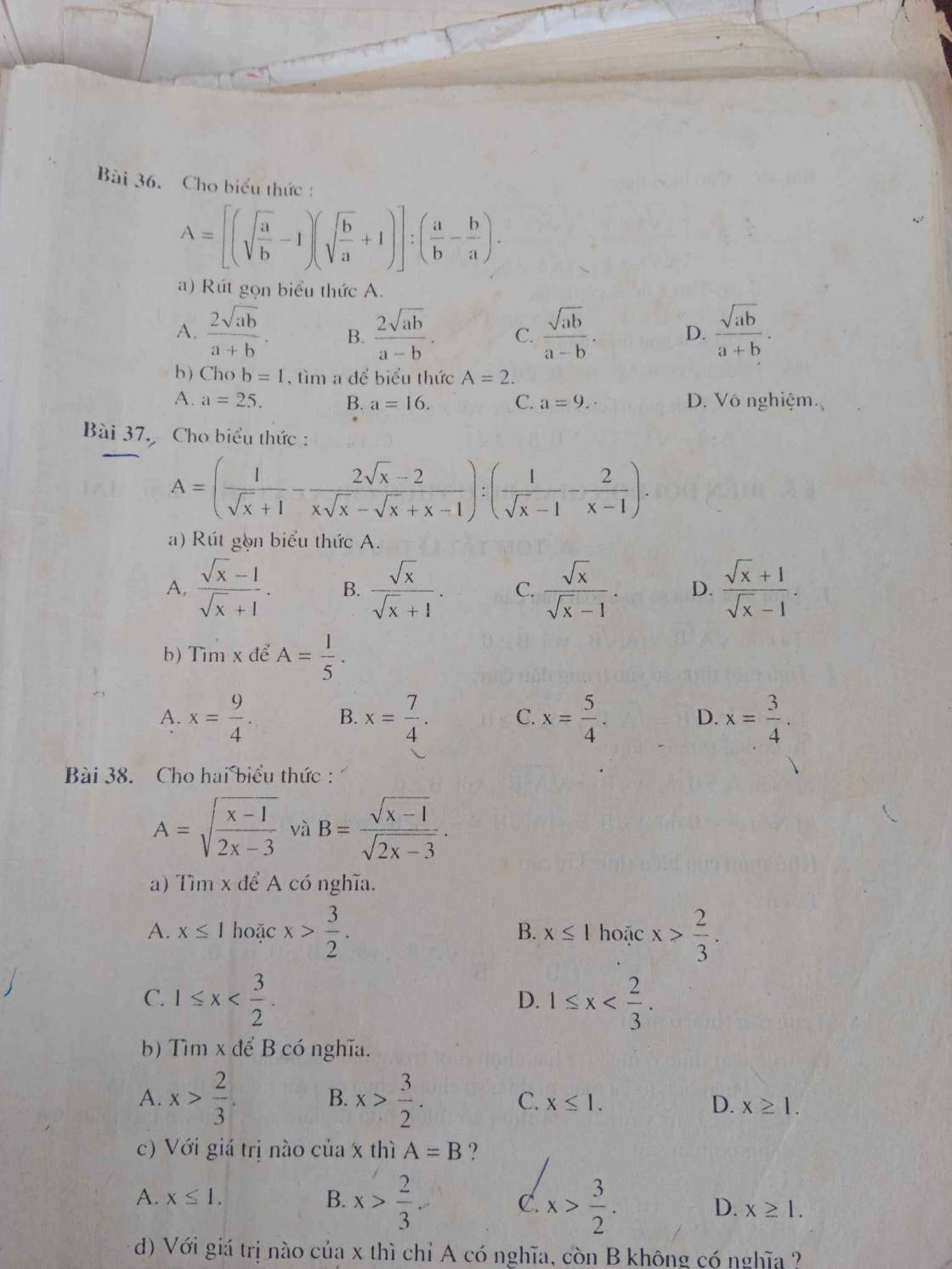
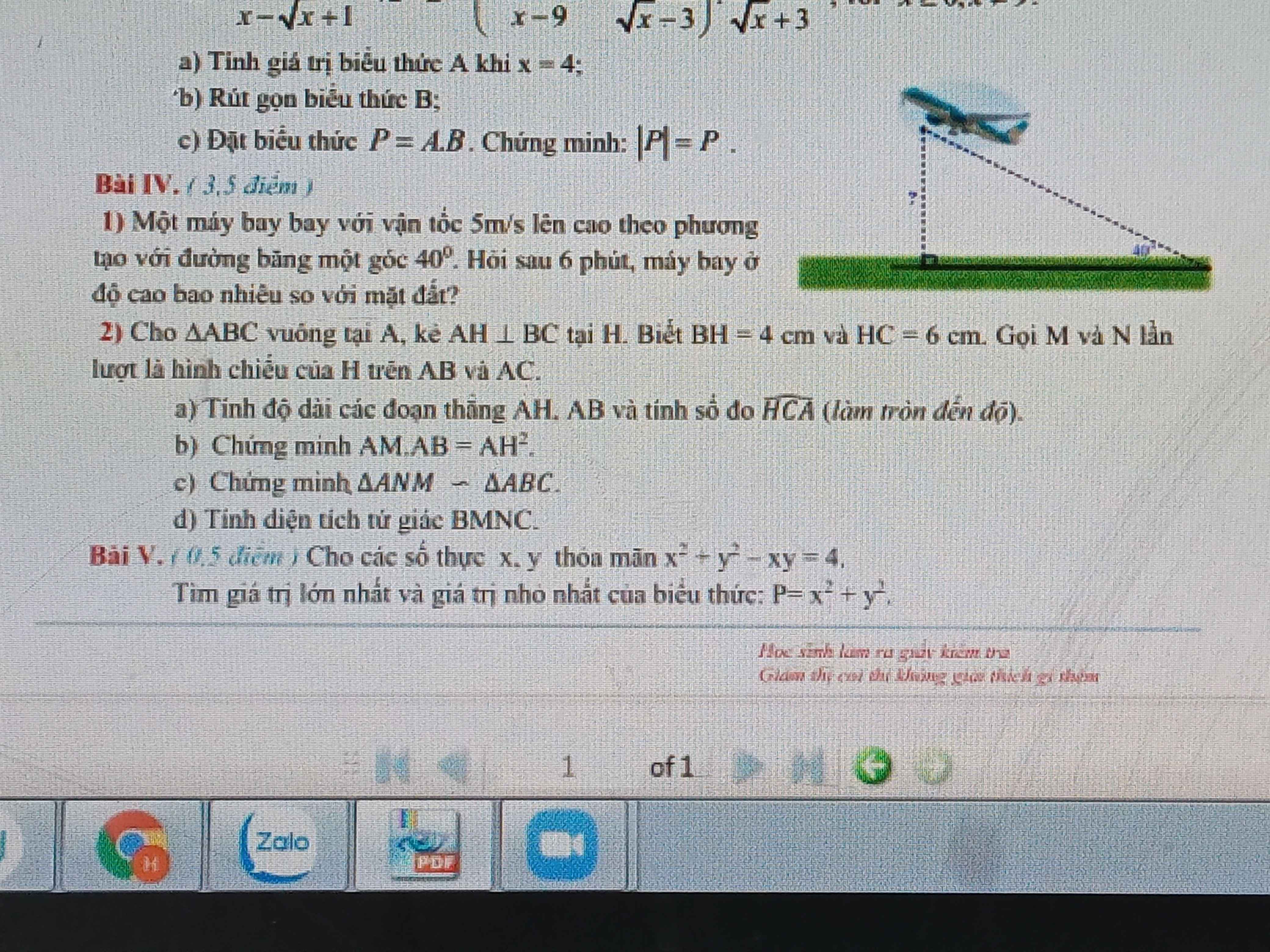


Bài 4:
a: \(M=\sqrt{a}+1+\sqrt{a}+1=2\sqrt{a}+2\)
mình hỏi bài 5 mà bạn