K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
3 tháng 3 2023
Ta có:
\(\Delta=b^2-4ac=\left(-m\right)^2-4.2.m\) \(=m^2-8m\)
Để phương trình có nghiệm thì \(\Delta\ge0\)
\(\Rightarrow m^2-8m\ge0\Leftrightarrow\left[{}\begin{matrix}m\le0\\m\ge8\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 1 2022
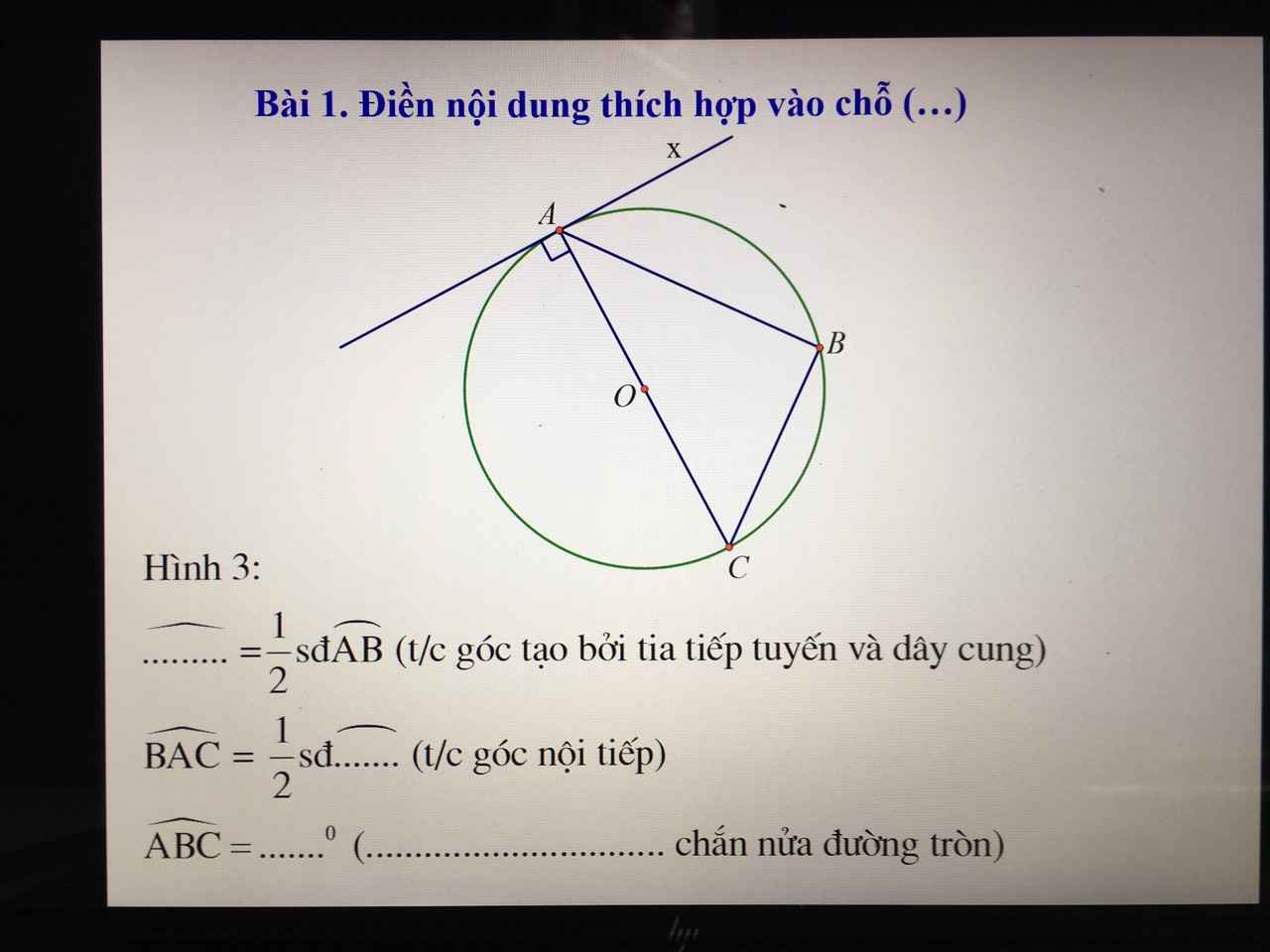
\(\widehat{BAx}=\dfrac{1}{2}sđ\stackrel\frown{AB}\)
\(\widehat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\)
\(\widehat{ABC}=90^0\) (góc nội tiếp chắn nửa đường tròn)
QN
0
TH
0
H
19 tháng 6 2023
Bài 1
Mình làm mẫu một số câu thôi nhé
\(9,\sqrt{5}=\left(\sqrt{5}\right)^2=5\\ \sqrt{6}=\left(\sqrt{6}\right)^2=6\)
Vì \(5< 6\)
\(\Rightarrow\sqrt{5}< \sqrt{6}\)
\(10,2\sqrt{5}=\left(2\sqrt{5}\right)^2=20\\ \sqrt{7}=\left(\sqrt{7}\right)^2=7\)
Vì \(20>7\)
\(\Rightarrow2\sqrt{5}>\sqrt{7}\)
\(11,5\sqrt{2}=\left(5\sqrt{2}\right)^2=50\\ 2\sqrt{3}=\left(2\sqrt{3}\right)^2=12\)
Vì \(50>12\Rightarrow5\sqrt{2}>2\sqrt{3}\)
\(12,2\sqrt{6}=\left(2\sqrt{6}\right)^2=24\\ 5=5^2=25\)
Vì \(25>24\Rightarrow5>2\sqrt{6}\)
\(13,\sqrt{7}=\left(\sqrt{7}\right)^2=7\\ 2=2^2=4\)
Vì \(7>4\Rightarrow\sqrt{7}>2\)
\(14,3=3^2=9\\ \sqrt{5}=\left(\sqrt{5}\right)^2=5\)
Vì \(9>5\Rightarrow3>\sqrt{5}\)
\(15,3\sqrt{6}=\left(3\sqrt{6}\right)^2=54\)
Vì \(54>1\Rightarrow3\sqrt{6}>1\)
\(16,2\sqrt{2}=\left(2\sqrt{2}\right)^2=8\\ 3=3^2=9\)
Vì \(8< 9\Rightarrow2\sqrt{2}< 3\)
Phương pháp làm dạng bài này là bình phương hai vế rồi so sánh
H
19 tháng 6 2023
Bài 2
Gợi ý : Biểu thức dưới dấu căn \(\ge\) 0
Lưu ý : Nếu biểu thức dưới dấu căn ở dưới mẫu thì \(>0\)
\(21,ĐK:4x^2-12x+9>0\\ \Rightarrow\left(2x-3\right)^2>0\\ \Leftrightarrow x\ne\dfrac{3}{2}\)
\(22,ĐK:x^2-8x+15\ge0\\ \Rightarrow\left[{}\begin{matrix}x\le3\\x\ge5\end{matrix}\right.\)
\(23,ĐK:\left\{{}\begin{matrix}x-2\ge0\\x-5\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge2\\x\ne5\end{matrix}\right.\)
\(24,ĐK:\left\{{}\begin{matrix}\dfrac{2+x}{5-x}\ge0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2+x\ge0\\5-x\ge0\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x\le5\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x< 5\end{matrix}\right.\left(t/m\right)\)
Hoặc
\(\left\{{}\begin{matrix}2+x\le0\\5-x\le0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\le-2\\x\ge5\\x\ne5\end{matrix}\right.\left(loại\right)\)
25 tháng 8 2021
Để A là số nguyên thì \(-5⋮2\sqrt{x}+1\)
\(\Leftrightarrow2\sqrt{x}+1\in\left\{1;5\right\}\)
\(\Leftrightarrow2\sqrt{x}\in\left\{0;4\right\}\)
hay \(x\in\left\{0;4\right\}\)
26 tháng 8 2021
Để A là số nguyên thì \(\sqrt{x}-1⋮2\sqrt{x}+3\)
\(\Leftrightarrow2\sqrt{x}+3-5⋮2\sqrt{x}+3\)
\(\Leftrightarrow2\sqrt{x}+3=5\)
\(\Leftrightarrow\sqrt{x}=1\)
hay x=1
HV
26 tháng 8 2021
\(A=\dfrac{x-7}{\sqrt{x}-2}-1\) để A nguyên thì \(\dfrac{x-7}{\sqrt{x}-2}nguyên\)
đặt \(\dfrac{x-7}{\sqrt{x}-2}=k\)(k nguyên)
tìm x theo k là ok
26 tháng 8 2021
Để A là số nguyên thì \(x-\sqrt{x}-5⋮\sqrt{x}-2\)
\(\Leftrightarrow x-2\sqrt{x}+\sqrt{x}-2-3⋮\sqrt{x}-2\)
\(\Leftrightarrow-3⋮\sqrt{x}-2\)
\(\Leftrightarrow\sqrt{x}-2\in\left\{-1;1;3\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{1;3;5\right\}\)
hay \(x\in\left\{1;9;25\right\}\)
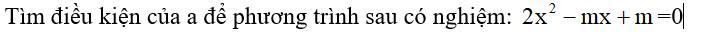
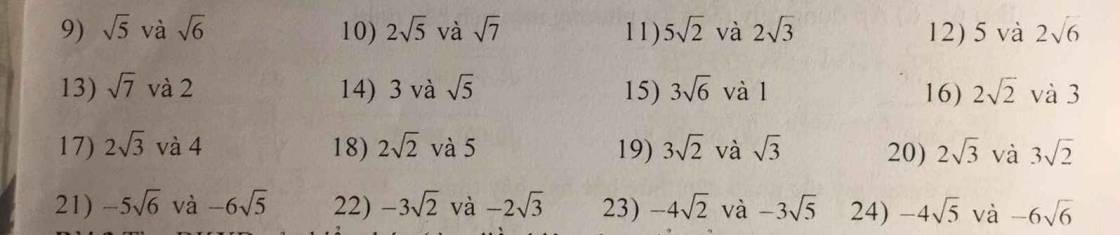
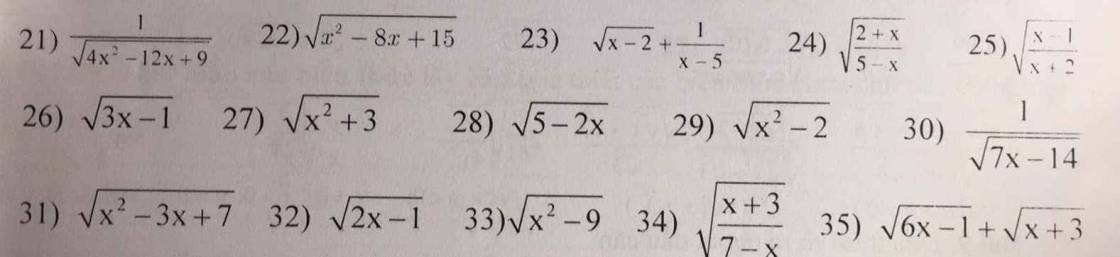
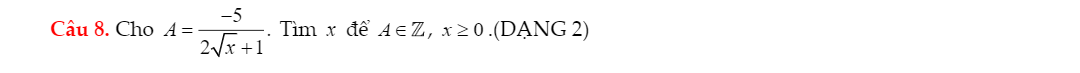
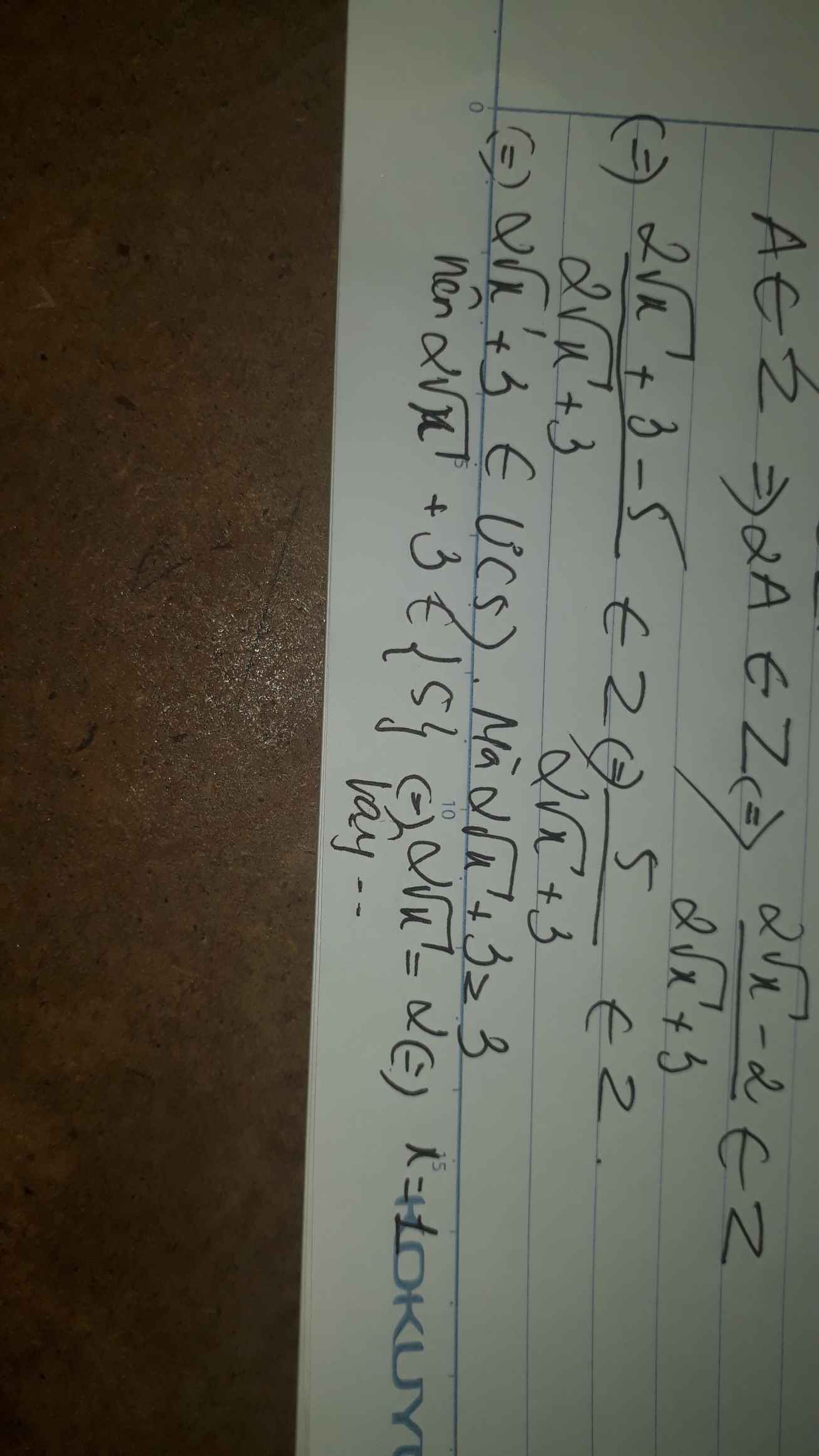
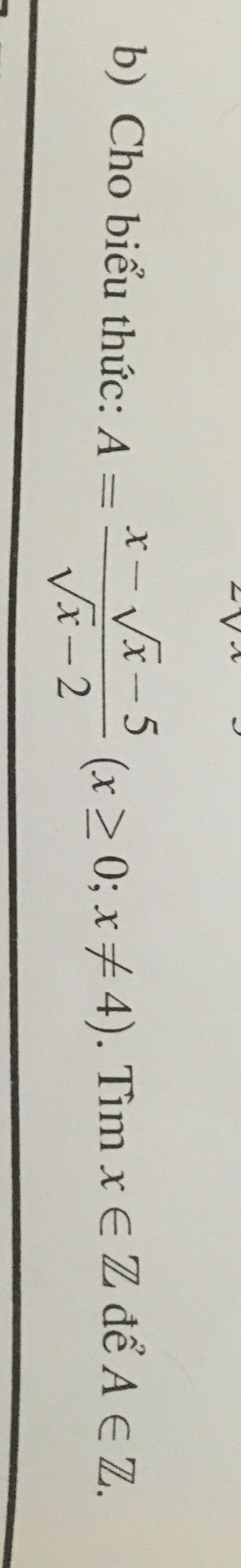
a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét ΔACE và ΔAFC có
góc ACE=góc AFC
góc CAE chung
=>ΔACE đồng dạng với ΔAFC
=>AC^2=AE*AF