K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 12 2021
e: \(E=\dfrac{x^2-9-x^2+4-x^2+9}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{x+2}{x+3}\)
a: \(A=\dfrac{4x^2+x^2-2x+1+x^2+2x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{6x^2+2}{\left(x-1\right)\left(x+1\right)}\)
11 tháng 1 2022
Bài 1:
b: \(\Leftrightarrow x^2-2x+4+x^3+8=12\)
\(\Leftrightarrow x^3+x^2-2x=0\)
=>x(x+1)=0
=>x=0 hoặc x=-1
f: \(\Leftrightarrow x+3-6x+12=-5\)
=>-5x=-20
hay x=4(nhận)
24 tháng 1
Câu 1:
a: 5x-2=3x+6
=>5x-3x=2+6
=>2x=8
=>\(x=\dfrac{8}{2}=4\)
b: a<=b
=>-2022a>=-2022b
=>-2022a+2021>=-2022b+2021
Câu 2:
1:
a: ĐKXĐ: x<>1
\(\dfrac{3}{x-1}+1=\dfrac{2x+5}{x-1}\)
=>\(\dfrac{3+x-1}{x-1}=\dfrac{2x+5}{x-1}\)
=>\(2x+5=x+2\)
=>x=-3(nhận)
b: |x-9|=2x-3
=>\(\left\{{}\begin{matrix}2x-3>=0\\\left(2x-3\right)^2=\left(x-9\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\\left(2x-3-x+9\right)\left(2x+3+x-9\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\\left(x+6\right)\left(3x-6\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\\left[{}\begin{matrix}x=-6\left(loại\right)\\x=2\left(nhận\right)\end{matrix}\right.\end{matrix}\right.\)
=>x=2
2:
\(\dfrac{x-3}{2}-\dfrac{3x+2}{4}< \dfrac{1}{3}\)
=>\(\dfrac{6\left(x-3\right)-3\left(3x+2\right)}{12}< \dfrac{4}{12}\)
=>6x-18-9x-6<4
=>-3x-24<4
=>-3x<28
=>\(x>-\dfrac{28}{3}\)
Câu 3:
Gọi độ dài quãng đường AB là x(km)
(Điều kiện: x>0)
Thời gian đi từ A đến B là \(\dfrac{x}{40}\left(giờ\right)\)
Thời gian ô tô đi từ B về A là \(\dfrac{x}{30}\left(giờ\right)\)
Theo đề, ta có phương trình:
\(\dfrac{x}{40}+\dfrac{x}{30}+\dfrac{1}{2}=9+\dfrac{1}{4}\)
=>\(\dfrac{7x}{120}=8,75\)
=>\(x=8,75:\dfrac{7}{120}=120\cdot1,25=150\left(nhận\right)\)
vậy: Độ dài quãng đường AB là 150km
21 tháng 4 2022
1/ Xét \(\Delta ABC\) và \(\Delta HAC\) có:
∠A = ∠AHC = 90 độ
∠C là góc chung
Do đó: △ABC ∼ △HAC (g . g)
2/ Ta có: \(\Delta HAC\sim\Delta ABC\)
\(\Rightarrow\dfrac{AC}{HC}=\dfrac{BC}{AC}\)
\(\Rightarrow AC.AC=HC.BC\)
\(\Rightarrow AC^2=HC.BC\) (đpcm)
3/ Đặt BD là x, theo tính chất đường phân giác, ta có:
\(\dfrac{AB}{AC}=\dfrac{BD}{DC}\Rightarrow\dfrac{9}{12}=\dfrac{x}{15-x}\)
\(\Rightarrow9\left(15-x\right)=12x\)
\(\Rightarrow135-9x=12x\)
\(\Rightarrow135=12x+9x\)
\(\Rightarrow135=21x\)
\(\Rightarrow x\approx6,4\)
Độ dài của DC là: \(15-x\Rightarrow15-6,4=8,6\)
Vậy BD = 6,4 cm và DC = 8,6 cm
PL
2
30 tháng 8 2021
Câu 3:
a: Ta có: \(2x\left(3x-1\right)-\left(x-3\right)\left(6x+2\right)\)
\(=6x^2-2x-6x^2-2x+18x+6\)
=14x+6
b: Ta có: \(2x\left(x+7\right)-3x\left(x+1\right)\)
\(=2x^2+14x-3x^2-3x\)
\(=-x^2+11x\)
30 tháng 8 2021
Câu 2:
a: Ta có: \(\left(-8x^5+12x^3-16x^2\right):4x^2\)
\(=-8x^5:4x^2+12x^3:4x^2-16x^2:4x^2\)
\(=-2x^3+3x-4\)
b: Ta có: \(\left(12x^3y^3-18x^2y+9xy^2\right):6xy\)
\(=12x^3y^3:6xy-18x^2y:6xy+9xy^2:6xy\)
\(=2x^2y^2-3x+\dfrac{3}{2}y\)
c: Ta có: \(\dfrac{x^3-11x^2+27x-9}{x-3}\)
\(=\dfrac{x^3-3x^2-8x^2+24x+3x-9}{x-3}\)
\(=x^2-8x+3\)
d: Ta có: \(\dfrac{6x^4-13x^3+7x^2-x-5}{3x+1}\)
\(=\dfrac{6x^4+2x^3-15x^3-5x^2+12x^2+4x-5x-\dfrac{5}{3}-\dfrac{10}{3}}{3x+1}\)
\(=2x^3-5x^2+4x-\dfrac{5}{3}-\dfrac{\dfrac{10}{3}}{3x+1}\)
AH
Akai Haruma
Giáo viên
11 tháng 9 2023
Câu 5:
a. $|x+\frac{4}{5}|-\frac{1}{7}=0$
$|x+\frac{4}{5}|=\frac{1}{7}$
$\Rightarrow x+\frac{4}{5}=\pm \frac{1}{7}$
$\Rightarrow x=\frac{-23}{35}$ hoặc $x=\frac{-33}{35}$
v.
$2x+5-(x-7)=18$
$2x+5-x+7=18$
$x+12=18$
$x=6$
c.
$2(x+1)+4^2=2^4$
$2(x+1)+16=16$
$2(x+1)=0$
$x+1=0$
$x=-1$
d.
$\frac{x-3}{x+5}=\frac{5}{7}$
$\Rightarrow 7(x-3)=5(x+5)$
$\Rightarrow 7x-21=5x+25$
$\Rightarrow 2x=46$
$\Rightarrow x=23$
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
11 tháng 9 2023
Câu 5:
\(a,\left|x+\dfrac{4}{5}\right|-\dfrac{1}{7}=0\\ \Leftrightarrow\left|x+\dfrac{4}{5}\right|=\dfrac{1}{7}\\ \Leftrightarrow\left[{}\begin{matrix}x+\dfrac{4}{5}=\dfrac{1}{7}\\x+\dfrac{4}{5}=-\dfrac{1}{7}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{7}-\dfrac{4}{5}\\x=-\dfrac{1}{7}-\dfrac{4}{5}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{23}{35}\\x=-\dfrac{33}{35}\end{matrix}\right.\\ b,2x+5-\left(x-7\right)=18\\ \Leftrightarrow2x-x=18-5-7\\ \Leftrightarrow x=6\\ c,2\left(x+1\right)+4^2=2^4\\ \Leftrightarrow2\left(x+1\right)=2^4-4^2=16-16\\ \Leftrightarrow2\left(x+1\right)=0\\ \Rightarrow x+1=0\\ \Leftrightarrow x=0-1=-1\\ d,\dfrac{x-3}{x+5}=\dfrac{5}{7}\left(x\ne-5\right)\\ \Leftrightarrow7\left(x-3\right)=5\left(x+5\right)\\ \Leftrightarrow7x-21=5x+25\\ \Leftrightarrow7x-5x=25+21\\ \Leftrightarrow2x=46\\ \Leftrightarrow x=23\)
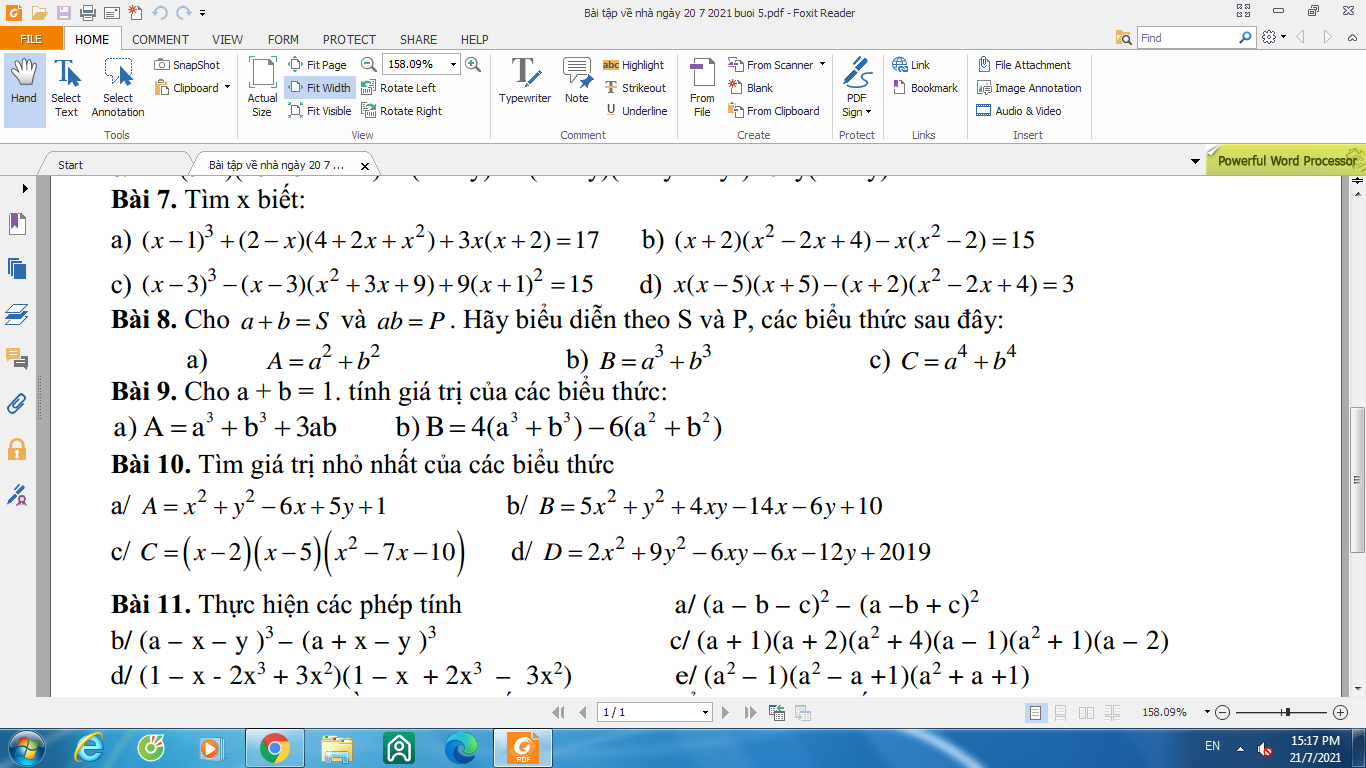
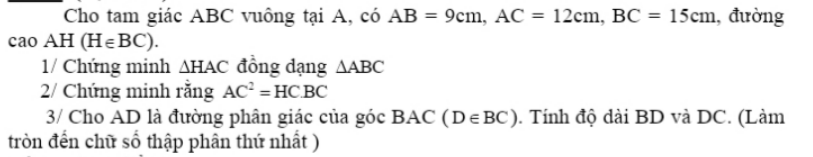
Bài 8
a, \(A=a^2+b^2=\left(a+b\right)^2-2ab\Rightarrow S^2-2P\)
b, \(B=a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)=\left(a+b\right)\left[\left(a+b\right)^2-3ab\right]\)
\(\Rightarrow S\left(S^2-3P\right)=S^3-3PS\)
c, \(C=a^4+b^4=\left(a^2+b^2\right)^2-2a^2b^2=\left[\left(a+b\right)^2-2ab\right]^2-2\left(ab\right)^2\)
\(\Rightarrow\left(S^2-2P\right)^2-2P^2\)
có thể giúp mik các bài còn lại đc ko