Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì tam giác IAB cân tại I nên tiếp tuyến phải song song với một trong 2 đường thẳng có phương trình \(y=x;y=-x\).
Ta có \(y'=\frac{1}{\left(x+2\right)^2}>0;x\ne-2\)
Mọi \(M\left(x_0;y_0\right)\) là tiếp điểm thì \(y'\left(x_0\right)=1\Leftrightarrow1=\frac{1}{\left(x_0+2\right)^2}\Leftrightarrow\left[\begin{array}{nghiempt}x_0=-1\\x_0=-3\end{array}\right.\)
Từ đó suy ra 2 tiếp tuyến là \(y=x+1;y=x+5\)

Đồ thị © có tiệm cận đứng là đường thẳng x=1 và tiệm cận ngang là đường thẳng y=2.Giao điểm của hai tiệm cận là I(1;2)
Gọi M(x0;2x0−3x0−1)∈©M(x0;2x0−3x0−1)∈©
Tiếp tuyến ΔΔ của đồ thị © tại M có phương trình
y=1(x0−1)2(x−x0)+2x0−3x0−11(x0−1)2(x−x0)+2x0−3x0−1
Giao điểm của ΔΔ với hai tiệm cận của đồ thị © là A(1;2x0−4x0−1)vàB(2x0−1;2)A(1;2x0−4x0−1)vàB(2x0−1;2)
ta có:IA=∣∣∣2x0−4x0−1−2∣∣∣=2|x0−1||2x0−4x0−1−2|=2|x0−1|
IB=2|x0−1|2|x0−1|
Do đó diện tích △IAB△IAB là: S=12IAIB=212IAIB=2
Gọi pp là nửa chu vi △IAB△IAB.Khi đó bán kính đường tròn nội tiếp △IAB△IAB là r=Spr=Sp=2p2p
rr lớn nhất khi pp nhỏ nhất
mặt khác,ta có :2p=IA+IB+AB=IA+IB+√IA2+IB2≥2√IAIB+√2IAIB=4+2√22p=IA+IB+AB=IA+IB+IA2+IB2≥2IAIB+2IAIB=4+22
Suy ra: pmin=2+√2pmin=2+2,dấu bằng xẩy ra ⇔IA=IB⇔2|x0−1|=2|x0−1|⇔[x0=0x0=2⇔IA=IB⇔2|x0−1|=2|x0−1|⇔[x0=0x0=2
với x0=0x0=0,phương trình tiếp tuyến cần tìm là Δ1Δ1:y=x+3
với x0=2x0=2,phương trình tiếp tuyến cần tìm là Δ2Δ2:y=x-1

+ Đồ thi hàm số đã cho co TCĐ là : x= -1 và TCN là y= 1; tâm đối xứng- giao của 2 đườg tiệm cận có tọa độ là I ( -1; 1)
Gọi M x 0 ; x 0 - 2 x 0 + 1 ∈ C , x 0 ≠ - 1 , I ( - 1 ; 1 )
+ Phương trình tiếp tuyến tại M có dạng
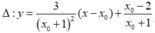
+ Giao điểm của ∆ với tiệm cận đứng là A - 1 ; x 0 - 5 x 0 + 1
+ Giao điểm của ∆ với tiệm cận ngang là B( 2x0+1; 1).
Ta có 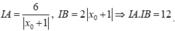
Bán kính đường tròn ngoại tiếp tam giác IAB là S=p.r, suy ra
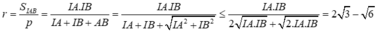
Suy ra,
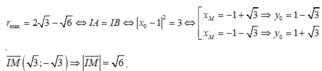
Chọn D.

Xét : \(M\left(x_0;x_0+1+\frac{1}{x_0+1}\right)\)
Tiếp tuyến tại M có phương trình \(y=\left(1-m^2\right)x+m^2+2m+1\) (với \(m=\frac{1}{x_0-1}\))
tiếp tuyến cắt tiệm cận đứng tại \(A\left(1;2m+2\right)\); cắt tiệm cận tại \(B\left(1+\frac{2}{m};2+\frac{2}{m}\right)\) và hai tiệm cận cắt nhau tại I(1;2)
Chu vi tam giác ABI : \(P=AB+BI+IA=\sqrt{4m^2+\frac{8}{m^2}+8}+\frac{2\sqrt{2}}{\left|m\right|}+2\left|m\right|\)
Áp dụng Bất đẳng thức Côsi, ta có :
\(4m^2+\frac{8}{m^2}\ge8\sqrt{2};\frac{2\sqrt{2}}{\left|m\right|}+2\left|m\right|\ge4\sqrt[4]{2}\Rightarrow P\ge\sqrt{8\sqrt{2}+8}+4\sqrt[4]{2}\)
Đẳng thức xảy ra \(\Leftrightarrow m=\pm\sqrt[4]{2}\)
Vậy \(M\left(1\pm\frac{1}{\sqrt[4]{2}};2\pm\frac{1}{\sqrt[4]{2}}\pm\sqrt[4]{2}\right)\)

+ Gọi M ( x 0 ; 2 + 3 x 0 - 1 ) ∈ C , x 0 ≠ 1 .
Phương trình tiếp tuyến tại M có dạng
∆ : y = - 3 x 0 - 1 2 ( x - x 0 ) + 2 + 3 x 0 - 1
+ Giao điểm của ∆ với tiệm cận đứng là A ( 1 ; 2 + 6 x 0 - 1 )
+ Giao điểm của ∆ với tiệm cận ngang là B( 2x0-1; 2).
Ta có S ∆ I A B = 1 2 I A . I B = 1 2 . 6 x 0 - 1 . 2 . x 0 - 1 = 2 . 3 = 6
Tam giác IAB vuông tại I có diện tích không đổi nên chu vi tam giác IAB đạt giá trị nhỏ nhất khi
IA=IB 
+Với x 0 = 1 + 3 thì phương trình tiếp tuyến là ∆ : y = - x + 3 + 2 3 . Suy ra
d O , ∆ = 3 + 2 3 2
+ Với x 0 = 1 - 3 thì phương trình tiếp tuyến là ∆ : y = - x + 3 - 2 3 . Suy ra
d O , ∆ = - 3 + 2 3 2
Vậy khoảng cách lớn nhất là 3 + 2 3 2 gần với giá trị 5 nhất trong các đáp án.
Chọn D.

Hàm số xác định với mọi \(x\ne1\). Ta có : \(y'=\frac{-4}{\left(x-1\right)^2}\)
Gọi \(M\left(x_0;y_0\right);\left(x_0\ne1\right)\) là tiếp điểm, suy ra phương trình tiếp tuyến của (C) :
\(\Delta:y=\frac{-4}{\left(x_0-1\right)^2}\left(x-x_0\right)+\frac{2x_0+2}{x_0-1}\)
a) Vì tiếp tuyến có hệ số góc bằng -4 nên ta có :
\(\frac{4}{\left(x_0-1\right)^2}=-16\Leftrightarrow\left[\begin{array}{nghiempt}x_0=\frac{3}{2}\\x_0=\frac{1}{2}\end{array}\right.\)
* \(x_0=\frac{3}{2}\Rightarrow y_0=10\Rightarrow\Delta=-16\left(x-\frac{3}{2}\right)+10\) hay \(y=-16x+22\)
* \(x_0=\frac{1}{2}\Rightarrow y_0=-6\Rightarrow\Delta=-16\left(x-\frac{1}{2}\right)-6\) hay \(y=-16x+2\)

\(f'\left(x\right)=2x+2\)
Gọi \(x_0\) là hoành độ tiếp điểm, do tiếp tuyến tạo với trục Ox một góc 45 độ
\(\Rightarrow\) Tiếp tuyến có hệ số góc bằng 1 hoặc -1
\(\Rightarrow\left\{{}\begin{matrix}f'\left(x_0\right)=2x_0+2=1\\f'\left(x_0\right)=2x_0+2=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_0=-\dfrac{1}{2}\Rightarrow y_0=\dfrac{1}{4}\\x_0=-\dfrac{3}{2}\Rightarrow y_0=\dfrac{1}{4}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=1\left(x+\dfrac{1}{2}\right)+\dfrac{1}{4}\\y=-1\left(x+\dfrac{3}{2}\right)+\dfrac{1}{4}\end{matrix}\right.\)

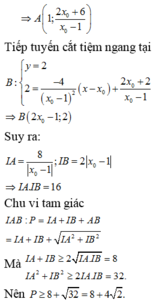
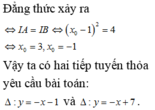
Lời giải:
Trước tiên, ta tìm được đồ thị hàm số $y$ có hai tiệm cận:
\(\bullet\) Tiệm cận đứng \(x=0\) (trục tung \(Oy\))
\(\bullet\) Tiệm cận xiên \(y=3-x\) \((d)\)
Xét hàm \(y=-x+\frac{1}{x}+3\Rightarrow y'=-1-\frac{1}{x^2}\)
Gọi \(a\) là hoành độ tiếp điểm. Khi đó, PT tiếp tuyến là:
\(y=\left ( -1-\frac{1}{a^2} \right )(x-a)-a+\frac{1}{a}+3\)
\(\Leftrightarrow \left ( 1+\frac{1}{a^2} \right )x+y-\frac{2}{a}-3=0\) \((m)\)
Gọi \(A=(d)\cap Oy\) thì \(A(0,3)\)
Gọi \(B=(m)\cap Oy\Rightarrow B(0,\frac{2}{a}+3)\)
Gọi \(C=(d)\cap (m)\). PT hoành độ giao điểm là:
\(-\left (1+\frac{1}{a^2}\right)x+\frac{2}{a}+3=3-x\Leftrightarrow \frac{2}{a}=\frac{x}{a^2}\Leftrightarrow x=2a\)
\(\Rightarrow C(2a,3-2a)\)
Do đó, \(AB=\left | \frac{2}{a} \right |\); \(BC=\sqrt{8a^2+\frac{4}{a^2}+8}\); \(AC=2\sqrt{2}|a|\)
Chu vi tam giác:
\(AB+BC+AC=\left |\frac{2}{a}\right|+2\sqrt{2}|a|+\sqrt{8a^2+\frac{4}{a^2}+8}=2(2+\sqrt{2})\)
\(\Leftrightarrow \left | \frac{1}{a} \right |+\sqrt{2}|a|+\sqrt{2a^2+\frac{1}{a^2}+2}=2+\sqrt{2}\)
Áp dụng BĐT Cô -si:
\(\left | \frac{1}{a} \right |+\sqrt{2}|a|\geq 2\sqrt{\sqrt{2}}>\sqrt{2}\)
\(a^2+\frac{1}{a^2}\geq 2\Rightarrow 2a^2+\frac{1}{a^2}+2\geq 4+a^2\geq 4\)
\(\Rightarrow \left | \frac{1}{a} \right |+\sqrt{2}|a|+\sqrt{2a^2+\frac{1}{a^2}+2}>2+\sqrt{2}\)
Do đó PT vô nghiệm, tức là không tồn tại $a$ nên không tồn tại PTTT.