K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LG
1
N
21 tháng 1 2022
\(MCD:\left(R_dntR1\right)//R2\)
\(->R_d=\dfrac{U_d^2}{P_d}=\dfrac{6^2}{3}=12\Omega\)
\(->R_{td}=\dfrac{\left(R_d+R1\right)\cdot R2}{R_d+R1+R2}=\dfrac{\left(12+6\right)\cdot6}{12+6+6}=4,5\Omega\)
\(->I=\dfrac{U}{R}=\dfrac{13,5}{4,5}=3A\)
\(->I_d=I1=\dfrac{P_d}{U_d}=\dfrac{3}{6}=0,5A\)
\(->I2=I-I_d1=3-0,5=2,5A\)
\(I_{AB}=I=3A\)
\(\left\{{}\begin{matrix}P_d=3\\P1=I1^2\cdot R1=0,5^2\cdot6=1,5\\P2=I2^2\cdot R2=2,5^2\cdot6=37,5\\P_{AB}=UI=13,5\cdot3=40,5\end{matrix}\right.\)(W)
Ta có: \(A//R1\)
\(=>U_A=U1=I1\cdot R1=0,5\cdot6=3V\)
\(=>I_A=\dfrac{U_A}{R_A}=\dfrac{3}{0}\) (vô lý)
NB
1
27 tháng 12 2023
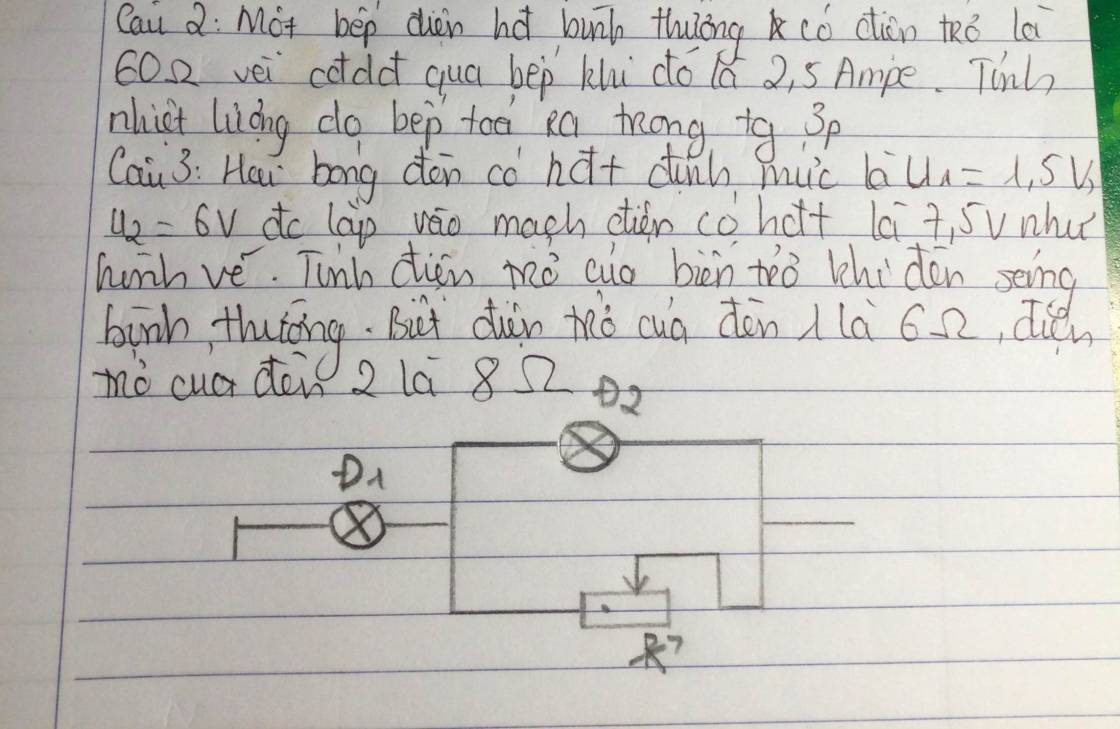
Câu 2.
Nhiệt lượng bếp tỏa ra trong thời gian \(t=3min=180s\) là:
\(Q=UIt=RI^2t=60\cdot2,5^2\cdot180=675000J\)
Câu 3.
\(I_{Đ1}=\dfrac{U_{Đ1}}{R_{Đ1}}=\dfrac{6}{6}=1A\)
\(I_{Đ2}=\dfrac{U_{Đ2}}{R_{Đ2}}=\dfrac{1,5}{8}=\dfrac{3}{16}A\)
\(I_b=I_{Đ1}-I_{Đ2}=1-\dfrac{3}{16}=\dfrac{13}{16}A\)
\(R_b=\dfrac{U_b}{I_b}=\dfrac{1,5}{\dfrac{13}{16}}=\dfrac{24}{13}\Omega\)
HK
1
HK
1
10 tháng 12 2021
Câu 1.
Khi mở khóa K:
\(I_m=I_1=0,4A\)
Khi đóng khóa K:
\(I_m=I_1+I_2=0,6\Rightarrow I_2=0,2A\)
\(U_1=0,4\cdot5=2V\)
\(\Rightarrow U_2=U_1=2V\)
\(\Rightarrow U=U_1=U_2=2V\)
\(R_2=\dfrac{U_2}{I_2}=\dfrac{2}{0,2}=10\Omega\)
12 tháng 10 2021
a) Do mắc song song nên:
\(U_{23}=U_3=U_2=I_2.R_2=0,5.6=3\left(V\right)\)
Cường độ dòng điện I3:
\(I_3=\dfrac{U_3}{R_3}=\dfrac{3}{9}=\dfrac{1}{3}\left(A\right)\)
Do mắc nối tiếp nên:
\(I=I_1=I_{23}=I_2+I_3=0,5+\dfrac{1}{3}=\dfrac{5}{6}\left(A\right)\)
b) \(R_{23}=\dfrac{R_2.R_3}{R_2+R_3}=\dfrac{6.9}{6+9}=3,6\left(\Omega\right)\)
\(R_{AB}=R_{23}+R_1=12+3,6=15,6\left(\Omega\right)\)
Hiệu điện thế U giữa 2 đầu đoạn mạch:
\(U=I.R_{tđ}=\dfrac{5}{6}.15,6=13\left(V\right)\)
A
nãy em chọn lộn môn hoá em xin lỗi ạ :> mọi ngừoi giúp em với em cần gấp ạ
3
1 tháng 11 2021
Câu 14:
\(R_{tđ}=R_1+R_2+R_3=12+15+13=40\left(\Omega\right)\)
\(I=I_1=I_2=\dfrac{U}{R}=\dfrac{12}{40}=0,3\left(A\right)\)
Câu 15:
\(R=\rho\dfrac{l}{S}=0,40.10^{-6}.\dfrac{10}{0,1.10^{-6}}=40\left(\Omega\right)\)
\(I=\dfrac{U}{R}=\dfrac{12}{40}=0,3\left(A\right)\)
TD
1
