
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


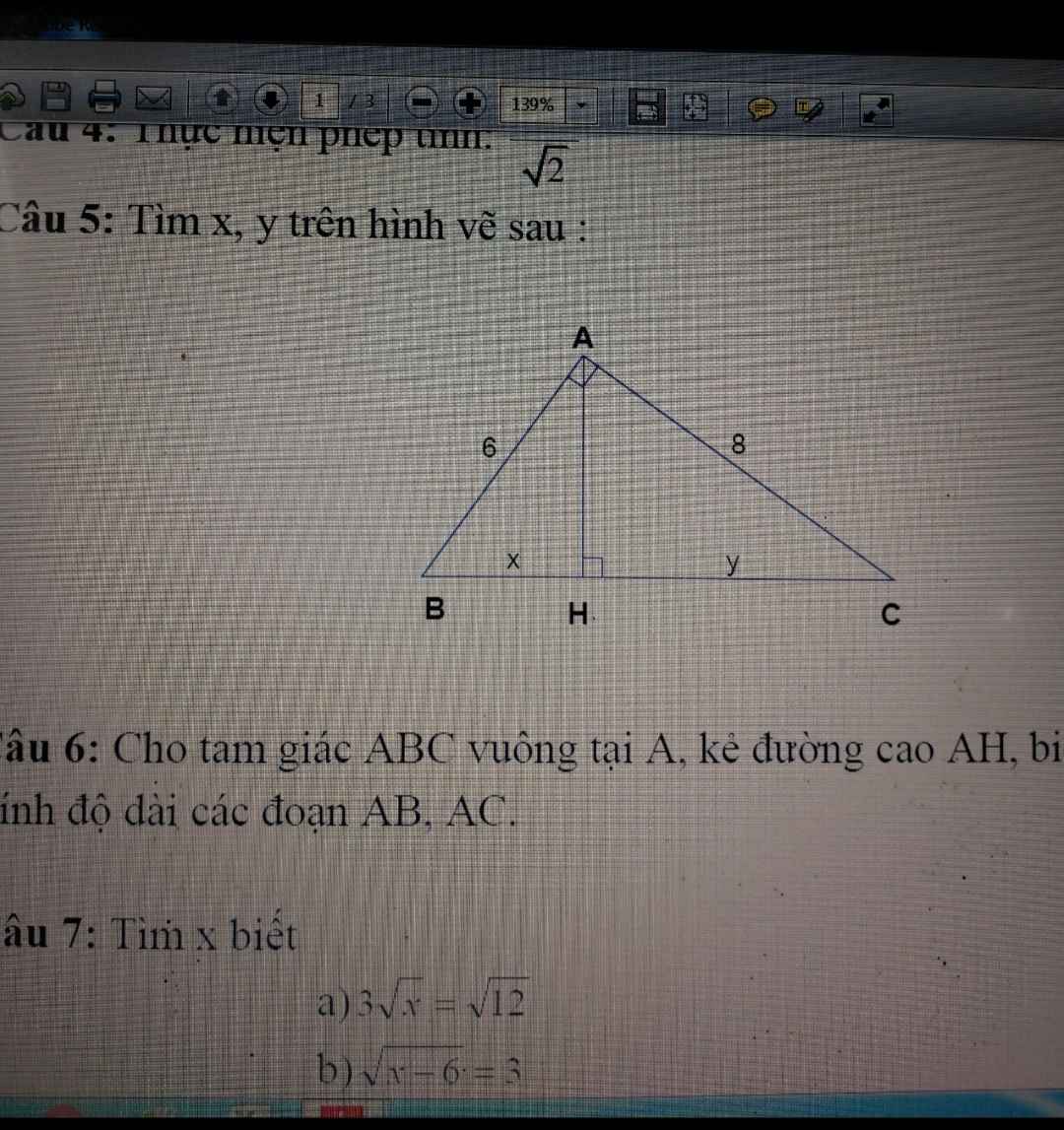
câu 5:
x=3,6
y=6,4
câu 6: chụp lại đề
câu 7:
a)ĐKXĐ: \(x\ge0\)
\(3\sqrt{x}=\sqrt{12}\\ \Rightarrow9x=12\\ \Rightarrow x=\dfrac{4}{3}\)
b) ĐKXĐ: \(x\ge6\)
\(\sqrt{x-6}=3\\ \Rightarrow x-6=9\\ \Rightarrow x=15\)

Bài 4:
a. ĐKXĐ: \(\left\{\begin{matrix} x-1\geq 0\\ x-1\neq 2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 1\\ x\neq 3\end{matrix}\right.\)
b. \(B=\frac{x-3}{\frac{x-1-2}{\sqrt{x-1}+\sqrt{2}}}=\sqrt{x-1}+\sqrt{2}\)
\(x=4(2-\sqrt{3})\Rightarrow x-1=7-4\sqrt{3}=(2-\sqrt{3})^2\)
\(\Rightarrow \sqrt{x-1}=2-\sqrt{3}\Rightarrow B=\sqrt{x-1}+\sqrt{2}=2-\sqrt{3}+\sqrt{2}\)
c.
$\sqrt{x-1}\geq 0$ với mọi $x\geq 1; x\neq 3$
$\Rightarrow B=\sqrt{x-1}+\sqrt{2}\geq \sqrt{2}$
Vậy $B_{\min}=\sqrt{2}$ khi $x=1$
Bài 5:
\(C=\frac{x-2\sqrt{xy}+y+4\sqrt{xy}}{\sqrt{x}+\sqrt{y}}-\frac{\sqrt{xy}(\sqrt{x}-\sqrt{y})}{\sqrt{xy}}\)
\(=\frac{(\sqrt{x}+\sqrt{y})^2}{\sqrt{x}+\sqrt{y}}-(\sqrt{x}-\sqrt{y})=(\sqrt{x}+\sqrt{y})-(\sqrt{x}-\sqrt{y})\)
\(=2\sqrt{y}\) vẫn phụ thuộc vào biến $y$ bạn ạ. Bạn xem lại đề.

Hệ có nghiệm duy nhất khi \(m^2\ne1\Rightarrow m\ne\pm1\)
Khi đó: \(\left\{{}\begin{matrix}x+my=m+1\\m^2x+my=3m^2-m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+my=m+1\\\left(m^2-1\right)x=3m^2-2m-1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{3m+1}{m+1}\\y=\dfrac{m-1}{m+1}\end{matrix}\right.\)
Đặt \(P=xy=\dfrac{\left(3m+1\right)\left(m-1\right)}{\left(m+1\right)^2}=\dfrac{3m^2-2m-1}{\left(m+1\right)^2}=\dfrac{-\left(m+1\right)^2+4m^2}{\left(m+1\right)^2}\)
\(=-1+\left(\dfrac{2m}{m+1}\right)^2\ge-1\)
\(P_{min}=-1\) khi \(m=0\)

b: \(BC=\sqrt{89}\left(cm\right)\)
\(\sin\widehat{B}=\dfrac{5\sqrt{89}}{89}\)
\(\Leftrightarrow\widehat{B}\simeq32^0\)
\(\widehat{C}=58^0\)

ĐKXĐ: x>=0; x<>9
\(B=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)
\(=\dfrac{-3\sqrt{x}-3}{\sqrt{x}+3}\cdot\dfrac{1}{\sqrt{x}+1}=\dfrac{-3}{\sqrt{x}+3}\)

a: Ta có: \(A=\sin^21^0+\sin^22^0+...+\sin^288^0+\sin^289^0\)
\(=\left(\sin^21^0+\sin^289^0\right)+...+\sin^245^0\)
\(=1+1+...+1+\dfrac{1}{2}\)
\(=\dfrac{89}{2}\)

Bài 1:
a: Ta có: \(2\sqrt{75}-\dfrac{1}{5}\sqrt{125}-\dfrac{1}{4}\sqrt{80}+\sqrt{605}\)
\(=6\sqrt{5}-\sqrt{5}-\sqrt{5}+11\sqrt{5}\)
\(=15\sqrt{5}\)
b: ta có: \(\dfrac{3}{\sqrt{2}-1}+\dfrac{3}{\sqrt{2}+1}-\sqrt{\left(4-3\sqrt{2}\right)^2}\)
\(=3\sqrt{2}+3+3\sqrt{2}-3-3\sqrt{2}+4\)
\(=3\sqrt{2}+4\)


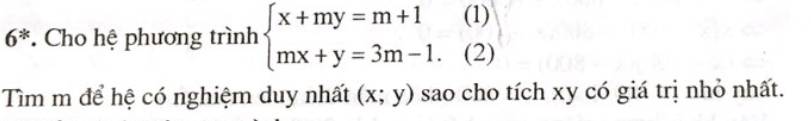

 Mọi người ơi,giúp em bài với ạ em cảm ơn ạ
Mọi người ơi,giúp em bài với ạ em cảm ơn ạ


Bài 6:
Ta có:
\(sin^2x+cos^2x=1\)
\(\Leftrightarrow cos^2x=1-sin^2x\)
\(\Leftrightarrow cos^2x=1-\left(\dfrac{1}{3}\right)^2=\dfrac{8}{9}\)
\(\Leftrightarrow cosx=\sqrt{\dfrac{8}{9}}=\dfrac{2\sqrt{2}}{3}\)
Mà: \(tanx=\dfrac{sinx}{cosx}\)
\(\Leftrightarrow tanx=\dfrac{1}{3}:\dfrac{2\sqrt{2}}{3}=\dfrac{1}{2\sqrt{2}}=\dfrac{\sqrt{2}}{4}\)
\(\Leftrightarrow\text{c}otx=\dfrac{1}{tanx}=1:\dfrac{\sqrt{2}}{4}=\dfrac{4}{\sqrt{2}}=2\sqrt{2}\)